По определению, анаморфоз — это конструкция,
созданная таким образом, что в результате оптического смещения некая
форма, недоступная поначалу для восприятия, складывается в легко
прочитываемый образ. Следовательно, анаморфоз — это проекция или
перспектива, на которую нужно смотреть с помощью особого устройства,
например цилиндрического или конического зеркала, либо с определенной
точки. Только в этом случае изображение примет требуемый вид. С помощью
компьютера можно исказить изображение так, что, взглянув на него в
цилиндрическое зеркало, мы увидим исходное изображение. Используем в
качестве примера обложку книги.
Преобразуем изображение так, что оно будет принимать
исходный вид в цилиндрическом зеркале диаметром 35 мм под углом зрения в
45°. Результат вы можете видеть на иллюстрации внизу слева. Если мы
правильно расположим зеркало, то получим изображение, показанное на
рисунке справа.
То, что сегодня легко выполняется с помощью
компьютера, ранее производилось путем разбиения картины на квадраты и
преобразования каждого квадрата в сектор кольца.
* * *
ИЗВЕСТНЕЙШИЙ АНАМОРФОЗ ВСЕХ ВРЕМЕН
Известнейший пример анаморфоза в живописи — это,
несомненно, «пятно», изображенное в нижней части картины «Послы» Ганса
Гольбейна Младшего.
Ганс Гольбейн Младший. «Послы» (1533). Лондонская национальная галерея.
Эта картина изобилует символами, связанными с
математикой. Персонажами картины являются Жан де Дентвиль (слева), в то
время посол Франции в Англии, который выступил заказчиком картины, и
Жорж де Сельв, епископ Лавура и друг Дентвиля, разделявший его увлечение
математикой. Сельв также был послом в Священной Римской империи,
Венеции и Ватикане, поэтому картина известна под названием «Послы». В
центральной части картины изображено множество предметов, указывающих на
увлечения персонажей. Эти предметы символизируют арифметику, геометрию,
музыку и астрономию, составлявшие так называемый квадривиум, и
грамматику, диалектику и риторику, из которых состоял так называемый
тривиум. Дисциплины, входившие в тривиум и квадривиум, именовались «семь
свободных искусств». Однако наибольшее внимание зрителя привлекает
пятно на полу. Оно словно висит в воздухе и выбивается из общей картины.
Это пятно является примером анаморфоза: достаточно наклониться и
посмотреть на картину искоса, и это пятно примет форму человеческого
черепа, который изображен в столь странной анаморфической перспективе.
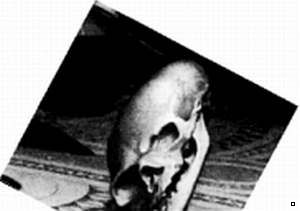 При взгляде под правильным углом «пятно» превращается в человеческий череп.
| 
