Альберти выполнил топографическую съемку Рима, однако составленная им карта не сохранилась. Результаты своей работы он изложил в книге, озаглавленной Descriptio Urbis Romae («Описание города Рима»), опубликованной в 1433 году незадолго до выхода трактата «О живописи». Эта книга начинается следующей фразой:

«С возможной тщательностью, при помощи придуманных мною математических приборов изучил я в том виде, в каком они нам известны сейчас, направления и очертания городских стен Рима, реки [Тибра] и дорог, равно как положение и размещение храмов, общественных зданий, ворот и трофеев, границы холмов и, наконец, площадь, занимаемую жилыми зданиями. Теперь всякий, не нуждаясь ни в каком особом даровании, удобно и легко сможет все вычертить в том масштабе, в каком ему заблагорассудится. К этому [описанию] склонили меня просвещенные друзья, и желание их я и счел нужным исполнить».

Рукопись «Описания города Рима» Альберти. XV век.

* * *

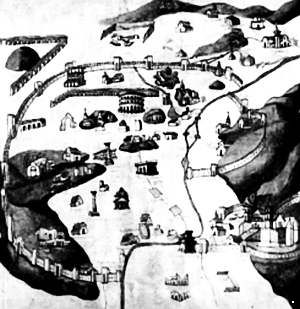
КАРТА РИМА ПЬЕТРО ДЕЛЬ МАССАЙО

Карта Альберти, которая предположительно была выполнена на основе результатов топографической съемки, приведенных в «Описании города Рима», не сохранилась. Тем не менее несколько лет спустя, в 1464 году, Пьетро дель Массайо опубликовал во Флоренции издание «Географии» Птолемея, в которое включил прекрасный план Рима, представленный на этой странице, который был выполнен по методу Альберти.

Можно заметить, что за исключением собора Святого Петра в Ватикане, изображенного внизу справа, и отдельных церквей Массайо прежде всего интересовали древние памятники: акведуки, Колизей, Пантеон, колонны Траяна и Марка Аврелия. Основной недостаток карты заключается в том, что из нее неясно, какую цель ставил перед собой автор — составить карту древнего Рима или же Рима середины кватроченто. Однако, несмотря на примитивность технических приспособлений, использованных при создании этой карты по методу Альберти, она является относительно точной, в чем легко убедиться, сравнив ее с любой современной картой.

* * *

Несколькими годами позже, примерно в 1450 году, Борсо д’Эсте, герцог Феррара, попросил его написать книгу, в которой бы излагались математические методы, использованные в «Описании города Рима». Так появилась книга «Математические забавы». Приведем фрагмент этой книги, в котором объясняется, как следует составлять схему определенного места. Для этого при помощи описываемого им инструмента следует произвести топографические измерения с трех различных точек и, используя подобие треугольников, построить карту местности.

Далее приводится перевод фрагмента этой книги со средневекового итальянского языка с максимально возможным соблюдением стиля Альберти:

«К сказанному мне хотелось бы прибавить описание одного инструмента, который весьма пригоден (как вы сами поймете) для подобных целей, в особенности для того, кто изготовляет баллисты и другие подобные военные машины. Однако я его применяю для целей гораздо более приятных: для топографического изучения местности или для съемки планов, как я это делал тогда, когда чертил план Рима. Итак, заодно я вам расскажу и об этом способе.

Вы определите расположение и охват территории с ее дорогами и домами таким образом. Сделайте на доске круг шириною не менее локтя [флорентийский локоть равнялся 58,4 см] и поделите весь этот круг на любое количество равных частей; чем больше их будет, тем лучше, потому что тогда они будут четки и ясны. Я обычно делю на 12 частей, проводя диаметры внутри круга; затем всю окружность изнутри я делю на 48 частей и эти 48 частей называю градусами. В свою очередь каждый из этих градусов я делю на 4 части и называю их минутами, а против каждого градуса проставляю соответствующую ему цифру, как на этом рисунке.

Гониометр Альберти. Иллюстрация из книги «Математические забавы».

Когда вы пожелаете вычертить свой план, вы поставите этот прибор на ровном месте, притом высоком, откуда вы можете окинуть взглядом много пунктов на той территории, план которой вы хотите начертить, вроде колоколен, башен и тому подобного. Затем вы возьмете веревку со свинцовой гирькой и отойдете от прибора на два локтя, поочередно визируя бросающиеся в глаза предметы так, чтобы линия вашего зрения, направляясь к башне, в которую вы целитесь взглядом, проходила одновременно через свинцовый отвес и через центр круга. Цифры, которые линия вашего зрения пересечет на окружности круга, направляясь к визируемой вами точке, запишите себе для памяти на бумаге.

Например, представьте себе, что вы находитесь со своим прибором на башне замка и визируете верхние ворота; предположим, что линия вашего зрения проходит около 20-го градуса, там, где обозначено деление в две минуты. Вы записываете на своем листке: верхние ворота — 20 градусов 2 минуты, и не двигая прибора, двигаетесь сами, визируя углы. Быть может, ваша визирная линия пройдет там, где на приборе обозначено 32 градуса и 0 минут. Тогда вы запишете: углы — 32. Так вы будете продолжать и дальше, не сдвигая прибора. Кончив это, перейдите в другое подобное место, видное с первого, и поставьте ваш прибор, расположив его так, чтобы под той линией, по которой вы первоначально визировали это место, оказалась именно та цифра, через которую эта линия проходила раньше. Иначе говоря, если бы от первой башни сюда плыл корабль, то при неизменном ветре он видел бы перед собою обозначение 20 градусов и 2 минуты, 32 градуса и тому подобное. Здесь вы поступаете так же, как в замке: обратите внимание на [цифры] внутри [окружности] и запишите их на другом листке.

Засим вы перейдете в третье место и там поступите так же, все замечая и все записывая. Здесь я помещаю для вас рисунок, поясняющий сказанное.

После этого вы поступите так. Возьмите вашу доску, на которой вы хотите вычертить план, и поставьте точку там, где вам покажется удобным, сообразуясь с общим расположением чертежа, и пусть это будет положение одного из тех мест, откуда вы наблюдали предметы. Например, пусть будет это замок. Напишите над этой точкой: замок. В этой точке прикрепите маленькую бумажную модель прибора шириною в полпяди, разделенную так же, как и самый прибор, с которым вы производили наблюдения, и расположите центр этой модели в точности над указанной точкой. Отсюда проведите все ваши линии на основании записей вашего памятного листка. Сходным образом поставьте, где вам заблагорассудится, вторую точку на только что проведенной вами линии, соответствующую второму из тех мест, откуда вы производили наблюдения, и на эту вторую точку наложите вторую бумажную модель, повернув ее так, чтобы указанной линии соответствовала та цифра, которая в вашем памятном листке стоит против слова «замок». Иными словами, чтобы обе модели лежали на линии, соответствующей им обеим, и чтобы все линии выходили отсюда в направлении тех цифр, которые обозначены на вашем листке.

И там, где линия вашей первой модели, соответствующая, например, Санто Доменико, пересекается с линией вашей второй модели, также соответствующей Санто Доменико, там поставьте точку и надпишите сверху: Санто Доменико. Также поступите и в отношении всех остальных. Если случится, что эти две линии пересекаются так, что угол оказывается не вполне ясным, поставьте модель в третьей точке, откуда вы производили наблюдения, и расположите ее подобно первым двум, чтобы линии их соответствовали друг другу, и благодаря этому все вам станет ясным. Подобные вещи нелегко выразить словами, но самый предмет нетруден и доставляет большое удовольствие, позволяя осуществить многое, как вы сами сможете убедиться.

Таким путем мне удалось отыскать древний акведук, который выходил наружу только некоторыми своими отдушинами, а ходы его были скрыты внутри горы. Таким путем, как вы понимаете, можно записать ходы и извивы любого лабиринта и пути в любой пустыне без погрешностей и ошибок.

Таким же способом вы можете измерить далекие расстояния. И если вы желаете измерить, каково расстояние между Торре дель Уччелино и замком, вы должны поступить следующим образом.

Поставьте ваш прибор так, как мы сказали, и заметьте цифру, под которой видна названная башня; затем визируйте какое-нибудь другое место, находящееся на известном расстоянии от вас; предположим, что вы находитесь на одном конце коридора в замке. Сделайте пометку на другом конце и визируйте ее, замечая градусы и минуты. Затем поставьте названный прибор на другой конец коридора, вами визированный, и расположите его так, как мы сказали, а именно чтобы прямая линия коридора соответствовала одной и той же цифре; отсюда визируйте названную башню и отметьте цифры на приборе. Сделав это, в зале или каком-либо другом помещении выберите площадку и пространство, на котором, как если бы вы хотели чертить план, обозначьте ваши точки и проведите линии при помощи вышеназванного прибора, отметив точки их пересечения, как показано на рисунке.

Я утверждаю, что столько раз, сколько расстояние между двумя названными точками содержится в любой из линий, выходящих из этих точек и пересекающихся друг с другом, столько раз промежуток между концами коридора содержится в расстоянии от любой из этих двух точек до Уччелино.

На рисунке вы увидите числовые обозначения, и для примера мы скажем, что от одной точки до другой — 35 унций [унция = 1/12 фута], а от пересечения обеих линий до одной из этих точек — 385 унций. Так как 35 содержится в 385 одиннадцать раз, то окажется, что в расстоянии между коридором и Торре дель Уччелино одиннадцать раз содержится промежуток, который вы брали в коридоре. Этот способ измерения будет вам служить на небольших расстояниях, а при расстояниях больших требуется прибор более крупный».