Прекрасным примером этих изменений в искусстве являются фрески капеллы Бранкаччи, над которыми он начал работу совместно с Мазолино да Паникале, впоследствии завершенные Филиппино Липпи. На стенах капеллы мы видим смешение стилей и постепенный переход от позднего средневековья Мазолино к возрождению Мазаччо и позднее к сочетанию этих направлений. В этом же стиле работал и Липпи.

В этом же духе Мазаччо задумал «Троицу» (заказчик неизвестен) — фреску огромных размеров на левой стене флорентийской церкви Санта-Мария-Новелла. Работы длились с 1426 по 1428 год.

Возможно, эта фреска стала для него последней, так как он скоропостижно скончался летом 1428 года во время путешествия в Рим в возрасте 27 лет, всего шесть из которых он активно занимался творчеством. Именно в «Троице» влияние метода перспективы Брунеллески прослеживается наиболее четко. Картина, изображенная на стене великолепной капеллы, нарисована так, что кажется зрителю абсолютно реальной.

Мазаччо. «Троица» (1426–1428).

В капелле, изображенной на картине, также прослеживается влияние архитектурного стиля Брунеллески, однако Мазаччо раскрасил арку в розовый цвет, отказавшись от традиционного для Брунеллески серого камня. По бокам этой арки, поддерживаемой двумя ионическими колоннами, расположены два коринфских пилястра с капителями такого же розового цвета. Капелла завершается бочарным сводом, украшенным квадратными кессонами.

Точка схода линий, изображенных в перспективе, расположена удивительно низко. Напомним, что она должна располагаться на уровне глаз зрителя, который входит в церковь и смотрит на картину. При ином расположении точки схода не возникает ощущения, что изображенная на картине капелла реальна. Также в перспективе изображены Дева Мария и Святой Иоанн, на которых, как и на купол, зритель смотрит снизу вверх. Они стоят параллельно колоннам и пилястрам, обрамляя центр композиции, где изображен Христос, распятый на кресте.

В верхней части композиции выделяется центральная ось симметрии, совпадающая с вертикальной линией креста. На ней располагается точка схода. Эта ось симметрии также делит пополам фигуру Бога Отца, протягивающего руки к креcту, и Святого Духа, изображенного в виде голубя, парящего между Христом и Богом Отцом. По обе стороны от этой оси симметрично относительно нее попарно расположены четыре фигуры: Дева Мария и Святой Иоанн — на переднем плане, поодаль — два коленопреклоненных донатора.

Композиция представляет собой равносторонний треугольник, символизирующий святую троицу. Не углубляясь в вопросы, связанные с геометрией композиции, заострим внимание лишь на некоторых из них, например на треугольнике, в основании которого изображены донаторы, а в вершине — голова Бога Отца. Другой треугольник образуют гвозди, которыми руки и ноги Христа прибиты к кресту. Еще один треугольник образуют глаза Марии, Христа и Святого Иоанна.

Более важным в нашем понимании является чередование синего и красного цветов, нарушающее доминирующую осевую симметрию, что придает картине динамичность и акцентирует внимание на глубине, умело переданной перспективным изображением архитектурных элементов.

Точка схода при изображении в перспективе расположена очень низко.

Некоторые примеры использования равносторонних треугольников при построении композиции.

Чередование синего и красного цветов в композиции.

Так, ярко-красный цвет туники и головного убора донатора слева внизу визуально соединяется с более нежным красным цветом одеяния Святого Иоанна справа; далее, вновь слева, — с цветом туники, накинутой на плечо Бога Отца, и, наконец, справа — с одним из красных кессонов, изображенных на потолке купола, которые чередуются с кессонами синего цвета в шахматном порядке. Таким образом передается восходящее движение, траектория которого сближается с осью симметрии.

Синий цвет симметрично чередуется с красным: воображаемая линия соединяет тунику донатора, одеяние Девы Марии, накидку на плече Бога Отца и заканчивается на кессоне синего цвета, симметричном предыдущему относительно центральной оси.

Осевая симметрия разбивается «смещением» чередующихся цветов, которые поднимаются вверх вдоль центральной оси симметрии.

Симметрия также нарушается в нижней части композиции, где изображен скелет, отделенный панелью алтаря. Надпись над ним гласит: Lo fu gia quel che voi sete: e quel chi son voi ancor sarete («Я был тем же, что и вы, но и вы станете тем же, чем стал я»).

Этот скелет и горсть земли под крестом отсылают к библейской традиции, по которой углями страстей Христовых были угли от дерева, выросшего на могиле Авеля.

Мы рассказали о первой оси симметрии, которая подчеркивает композицию и акцентирует ее силу. Другая ось, перпендикулярная ей, на которой расположены коленопреклоненные донаторы, определяется пересечением плоскости алтаря с картинной плоскостью. Третья ось, перпендикулярная первым двум, несомненно, является главным лучом зрения наблюдателя, глаза которого расположены на той же высоте, что и точка схода.

Плоскости, перпендикулярные последней оси, четко отделяют друг от друга три плана картины. На ближнем плане, снаружи арки, преклонили колени донаторы.

Далее изображены три библейских персонажа: Святой Иоанн, Дева Мария и Христос, которые располагаются на одну ступень выше. Далее, в глубине картины, вблизи оси симметрии и чуть выше, растворяясь в фоне, изображены голубь и Бог Отец, протягивающий руки к кресту, стоящий на возвышении красного цвета.

Если мы будем трактовать эти оси как декартовы оси координат, то есть перенесемся из XV века, когда жил Мазаччо, в XVII, во времена Декарта, и обозначим за у ось, расположенную в глубине картины, то каждая из трех описанных нами плоскостей будет задаваться уравнением вида у = k_j, где j = 1, 2 и 3. Так, плоскость, на которой находятся донаторы, будет задаваться уравнением у = k₁, плоскость креста — у = k₂; плоскость, на которой изображен Бог Отец, — у = k₃

Каждой плоскости соответствуют разные моменты времени. Можно установить, что k₁ соответствует 1428 год (см. иллюстрацию слева), когда Мазаччо завершил работу и когда жили донаторы, оплатившие ее. Плоскость k₂ соответствует 33 году (очевидно, после Рождества Христова), когда, по Библии, был распят Христос (см. центральную иллюстрацию). Значение k₃  определяющее положение плоскости, на которой изображен Бог Отец, с точки зрения богословия корректнее принять равным 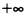 (см. иллюстрацию справа).

Рассечение пространства картины «Троица» Мазаччо плоскостями, параллельными картинной плоскости и перпендикулярными временной оси. Слева — плоскость, датируемая 1428 годом; в центре — плоскость, датируемая 33 годом; справа — бесконечно удаленная плоскость.

Однако мы перечислили не все временные плоскости. Существует и четвертая, задаваемая уравнением у = k₀, которая на первый взгляд остается незамеченной.

Как следует из уравнения этой плоскости, она параллельна предыдущим и картинной плоскости и, как следствие, перпендикулярна временной оси. На ней располагается зритель, пришедший посмотреть на «Троицу» в церковь Санта-Мария-Новелла во Флоренции. Мы находимся ниже остальных героев картины, то есть в соответствии с нашим положением: ниже богов и знати. Уравнение этой плоскости в соответствии с вышеизложенным будет выглядеть как у = 2014 (где 2014 — год, в котором мы смотрим на картину).

Однако когда мы смотрим на «Троицу» Мазаччо, изображенную на страницах этой книги, то находимся в некотором роде на другой плоскости, также виртуальной, которую можно в метафорическом смысле считать симметричной плоскости, на которой изображен Святой Дух, относительно картинной плоскости. Мы как читатели находимся в некоторой неопределенной точке, координата которой стремится к 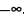. Мазаччо гениальным образом предвидел это: он включил нас в картину не просто как зрителей, но как персонажей, которые наблюдают за ней и занимают определенное место в композиции.

* * *

МАЗАЧЧО, ТЕРРИБИЛИТА И ПЕРСПЕКТИВА

Художник эпохи кватроченто Томмазо ди сер Джованни ди Гвиди, которого все называли Мазаччо (1401–1428), прожил недолгую жизнь, но сыграл решающую роль в истории искусства. Считается, что он первым применил в живописи законы перспективы, открытые Брунеллески. Мазаччо родился в Ареццо и в пять лет остался сиротой. Начав обучаться живописи в родном городе, в котором он создал свои первые работы, он переехал во Флоренцию, где подружился с Донателло и Брунеллески, а также с представителями гуманистической среды города.

Первая работа, приписываемая Мазаччо, — триптих из церкви Святого Ювеналия, датируемый 23 апреля 1422 года. Вскоре Мазаччо совместно с Мазолино начал работу над фресками капеллы Бранкаччи церкви Санта Мария дель Кармине. В 1426–1428 годах он создал фреску «Троица» в церкви Санта-Мария-Новелла. В 1428 году он переехал в Рим по приглашению кардинала Бранда Кастильоне, который поручил ему украсить церковь Сан Клементе, бросив работу в капелле Бранкаччи, которую 70 лет спустя завершил Филиппино Липпи. В Риме он работал над полиптихом для церкви Санта-Мария-Маджоре, из которого до нас дошла картина «Святой Иероним и Иоанн Креститель», находящаяся в настоящее время в Лондонской национальной галерее. Мазаччо умер в Риме осенью 1428 года.

Работы Мазаччо выделяются тем, что в них используется научный подход к перспективе. В рамках этого подхода понятию пространства придается новое значение. Математическая перспектива вкупе с экспрессивностью персонажей и особой работой со светом входит в число важнейших элементов художественного языка эпохи Возрождения.

Автопортрет Мазаччо в капелле Бранкаччи, Флоренция.

_{(фотография: FMC)}