Открытия немецкого математика Феликса Хаусдорфа впоследствии позволили сформировать современную теорию фракталов.

Хаусдорф счел классическое определение размерности объектов очень узким как с математической, так и с философской точки зрения, а классификацию тел согласно их размерности — примитивной. Он сказал, что будет несколько затруднительно и, возможно, даже некорректно считать, что объект имеет размерность 1, если он имеет только длину (например, нить или пружина), размерность 2 — если он имеет длину и ширину (лист бумаги или поверхность сферы), и размерность 3, если, помимо длины и ширины, он имеет высоту (сфера или коробка для обуви). Чтобы расширить классическое понятие размерности, Хаусдорф предложил новое определение, более сложное и общее с математической точки зрения.

Величина, введенная Хаусдорфом, позволяет намного точнее определить размерность объекта. Вопреки тому, что нам подсказывают органы чувств, существуют объекты, размерность которых выражается дробями, например 1/2, иррациональными числами, в частности √5, и даже еще более необычными числами. Прошло больше 50 лет с момента, когда Хаусдорф ввел новое понятие размерности, прежде чем Бенуа Мандельброт (1924–2010), французский математик польского происхождения, определил фракталы как множества, имеющие дробную размерность Хаусдорфа.

Бенуа Мандельброт, математик, который ввел термин «фрактал». На этой фотографии он изображен на конференции в Варшаве в 2005 году.

Чтобы объяснить понятие размерности Хаусдорфа в общем виде (именно это определение привел сам Хаусдорф), потребуются серьезные знания математики. Тем не менее существует альтернативное определение, не до конца точное, но позволяющее читателю оценить смысл этого понятия. Это альтернативное определение размерности ввели русские математики Лев Понтрягин и Лев Шнирельман. Удивительно, что Понтрягин был слепым — он лишился зрения в 14 лет в результате несчастного случая.

Представьте, что дана плоская фигура, вписанная в квадрат, для которой мы хотим рассчитать размерность Хаусдорфа. Разделим сторону квадрата на несколько равных частей, например на 10. Квадрат окажется разделен на 100 мелких квадратов. Теперь посчитаем, сколько этих квадратов нужно для того, чтобы покрыть рассматриваемую фигуру, и адекватно сравним их число с числом частей, на которые мы разделили сторону квадрата (в нашем случае на 10).

Ключ к задаче — в том, что мы вкладываем в слова «адекватно сравним». Проясним смысл этих слов на простом примере. Пусть рассматриваемой фигурой будет квадрат целиком. Для того чтобы покрыть его, потребуются все квадраты, на которые мы разделили исходный квадрат. Таким образом, если мы разделим сторону квадрата на n равных частей, получим n·n = n² мелких квадратов. Обратите внимание на число 2 в показателе степени n² — именно это число и будет размерностью квадрата.

Теперь рассмотрим диагональ квадрата. Разделим сторону квадрата на 4 части. Сколько мелких квадратов понадобится для того, чтобы покрыть его диагональ? Немного подумав, читатель увидит, что для этого потребуется четыре мелких квадрата, так как именно столько квадратов лежит на диагонали большого квадрата. Если мы разделим сторону квадрата на n частей, нам потребуется n квадратов, чтобы покрыть диагональ. Однако n можно записать как n¹, то есть n, возведенное в степень 1. Эта степень 1 и будет размерностью диагонали квадрата. Таким образом, любой отрезок будет иметь размерность 1.

Теперь обозначим через F плоскую фигуру, заключенную внутри квадрата, для которой мы хотим определить размерность Хаусдорфа. Разделив сторону квадрата на n частей, подсчитаем, сколько мелких квадратов потребуется, чтобы покрыть фигуру F. Обозначим их число через пр. «Адекватное» сравнение числа n_F с числом частей n, на которые мы разделили сторону квадрата, означает определение степени n, соответствующей этому числу n_F. Так, в примере с квадратом n_F  = n² соответствующей степенью будет 2. В примере с диагональю квадрата n_F  = n¹ соответствующей степенью будет 1. Если мы обозначим этот показатель степени через d, то n, n_F и d будут связаны следующим тношением: n_F = n^d . Применив логарифмы, выразим d через n и n_F : d — это логарифм n_F разделенный на логарифм n:

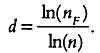
Чем больше n, то есть число частей, на которые мы делим сторону квадрата, тем ближе число d будет к размерности Хаусдорфа для фигуры F. Размерность Хаусдорфа будет пределом, рассчитываемым при делении стороны квадрата на бесконечно большое число бесконечно малых равных частей.

Пример с окружностями Аполлония

Построим пример фрактала. Для этого вновь рассмотрим окружности Аполлония, о которых мы говорили в главе 2, так как мы будем строить фрактал на основе касательных окружностей. Построим три окружности, касающиеся друг друга (см. рисунок слева внизу). Как мы уже отмечали в предыдущей главе, существуют две другие окружности, касающиеся этих трех. Имеем пять окружностей (см. рисунок справа внизу).

Построение фрактала на основе трех касающихся окружностей.

Выберем три из них, касающиеся друг друга, и построим две соответствующие касательные окружности (их существование следует из теоремы Аполлония). В конечном итоге, с учетом повторений, получим шесть новых окружностей. Вкупе с пятью исходными имеем 11 окружностей (см. рисунок слева внизу). Повторим построение для этих 11 окружностей, затем — для окружностей, построенных на следующем этапе (см. рисунок справа внизу), и так далее до бесконечности. Полученные окружности носят название «ковер Аполлония» и представляют собой пример фрактала.

Построение фрактала на основе трех касающихся окружностей.

Сложно представить, что неимоверно сложный ковер Аполлония образуется простым построением окружностей, касающихся друг друга. Если читатель использует воображение, то увидит, что каждая окружность на ковре Аполлония находится среди бесконечного множества касательных окружностей, за исключением внешней, которая содержит в себе все прочие окружности. Более того, на любой дуге любой окружности, сколь малой бы она ни была, находится бесконечно много касающихся ее окружностей. Стандартное обозначение размерности абсолютно неприменимо для описания ковра Аполлония: было бы излишне говорить, что эта кривая имеет размерность 2, то есть ту же размерность, что и содержащая ее плоскость. Тем не менее, учитывая сложность этой кривой, в которой произвольной дуги любой окружности касается бесконечное множество окружностей, было бы преуменьшением сказать, что ее размерность равна 1. Вычислить точную размерность Хаусдорфа для ковра Аполлония невероятно сложно. На данный момент известно лишь ее приближенное значение, равное 1,305688.

Этот ковер Аполлония колоссальных размеров изобразил художник Джим Деневан в пустыне штата Невада.

Пример на основе треугольника

Построим другой фрактал, для которого можно точно определить размерность Хаусдорфа. Это кривая Коха, названная в честь шведского математика Нильса фон Коха, определившего ее в 1906 году. Существует несколько разновидностей этой кривой.

Мы построим кривую Коха, взяв за основу равносторонний треугольник. Для этого разделим каждую его сторону на три равные части и заменим центральный отрезок на каждой стороне двумя сторонами равностороннего треугольника, основанием которого будет этот отрезок. Получим шестиконечную звезду. Повторим построение снова, то есть разделим каждую из двенадцати сторон звезды на три равные части и заменим центральный отрезок на каждой стороне двумя сторонами равностороннего треугольника, основанием которого будет этот отрезок. Для построения кривой Коха эти действия нужно повторить бесконечное число раз.

Четыре первых этапа построения кривой Коха.

Теперь представьте, что кривая Коха — это дорога. Рассмотрим две любые точки на этой кривой (представьте, что это две деревни, расположенные у дороги). Сядем в воображаемую машину и поедем из одной деревни в другую вдоль кривой. Какое расстояние покажет счетчик пробега в конце пути? Если читатель ответит, что расстояние будет зависеть от выбранных точек кривой, то ошибется: независимо от того, какие точки мы выберем, пройденное расстояние всегда будет равно бесконечности.

Иными словами, любой участок кривой Коха имеет бесконечно большую длину — она содержит так много поворотов, что проехать по ней от начала до конца невозможно (см. врезку на следующей странице). Похожими свойствами обладает дорога, проходящая вдоль побережья Галисии в Испании. Расстояние, отделяющее устье реки Миньо и мыс Эстака де Барес, по прямой составляет чуть больше 200 километров. Но попытайтесь проделать этот путь, следуя вдоль побережья, и он покажется вам бесконечным: автомагистраль будет петлять возле каждой реки, идти в объезд всех гор, мысов и заливов. Десять километров, разделяющие устье реки и мыс, превращаются в сто и даже больше, и путь кажется бесконечным. Именно это (пусть и в несколько преувеличенном виде) произойдет, если мы попытаемся проехать вдоль кривой Коха.

* * *

ДЛИНА КРИВОЙ КОХА

Чтобы убедиться, что кривая Коха имеет бесконечную длину, выполним следующие действия. Заметим, что на каждом шаге построения кривой Коха число отрезков, составляющих ее, увеличивается в 4 раза: каждый из отрезков, построенных на предыдущем шаге, делится на три части, одна из которых заменяется двумя отрезками. Иными словами, на смену каждому отрезку приходит четыре. Так как построение начинается с равностороннего треугольника, общее число отрезков на шаге N будет равно 3·4^N. По той же причине длина каждого из этих отрезков (все они имеют одинаковую длину) на каждом шаге делится на 3, поэтому на шаге N длина каждого ее отрезка будет равна I/3^N, где I — длина стороны исходного равностороннего треугольника. Длина кривой на шаге N будет равна числу образующих ее отрезков, умноженному на их длину:

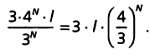
Так как 4/3 больше 1, степень (4/3)^N с увеличением N будет неограниченно возрастать и в итоге будет равна бесконечности. Аналогичным образом можно убедиться, что любая часть кривой Коха имеет бесконечную длину.

* * *

Как и в случае с ковром Аполлония, стандартная размерность совершенно не подходит для описания кривой Коха: нельзя говорить, что эта кривая имеет размерность 2, то есть ту же размерность, что и содержащая ее плоскость; однако учитывая сложность этой кривой, произвольный участок которой имеет бесконечно большую длину, было бы ошибкой полагать, что ее размерность равна 1. Размерность Хаусдорфа позволяет в точности понять, в какой степени кривая Коха сочетает в себе кривую и поверхность. Ее размерность равна ln4/lnЗ (см. врезку на следующей странице).

Мандельброт показал, что геометрия фракталов может быть невероятно сложной, однако очень часто эту сложность порождает простое подобие различных частей кривой, сохраняющееся вне зависимости от масштаба.

* * *

ФРАКТАЛЬНАЯ РАЗМЕРНОСТЬ КРИВОЙ КОХА

Вычислить фрактальную размерность кривой Коха сравнительно просто. Напомним, что общее число отрезков этой кривой на шаге N равно 3·4^N, а длина каждого из этих отрезков равна I/3^N (см. предыдущую врезку). Учитывая особенности построения кривой, впишем ее в квадрат со стороной I (где I — длина стороны исходного треугольника). Будем делить квадрат на равные части так, чтобы их число отвечало степени тройки: сначала на 3 части, затем на 3·3 = 3² частей, затем на 3·3·3 = 3³ и так далее. Теперь подсчитаем, сколько маленьких квадратов необходимо для покрытия кривой Коха, если мы разделим сторону исходного квадрата, например, на 3^N частей. Для этого заменим кривую Коха кривой, полученной на N-м шаге построения. Так как длина стороны маленького квадрата равна I/3^N, каждый из них покроет примерно один отрезок кривой, который также имеет длину I/3^N. Так как число отрезков кривой равно 3·4^N, нам потребуется примерно 3·4^N маленьких квадратов. Согласно определению размерности Хаусдорфа, мы разделили сторону квадрата на n = 3^N частей, а для покрытия всей кривой требуется n_F = 3·4^N маленьких квадратов. Используем свойства логарифмов, чтобы упростить дробь, определяющую размерность Хаусдорфа:

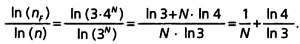
Когда число частей, на которое мы делим квадрат, то есть n, или, что аналогично, N, становится бесконечно велико, размерность Хаусдорфа будет равна ln4/lnЗ.

* * *

Фракталы — редкие, удивительные множества, которые, как «кажется», далеки от привычных нам физических ощущений. Мы взяли слово «кажется» в кавычки, поскольку фракталы присутствуют повсеместно, мы видим их так часто и настолько привыкли к их особенностям, что даже не распознаем их. В природе фрактальная геометрия обнаруживается буквально повсюду. Береговая линия Испании или Норвегии, изрезанная фьордами, точнее всего описывается именно фрактальной кривой, подобной кривой Коха. Ничто не описывает сложную сеть нейронов нашего мозга лучше, чем фракталы. Именно математический взгляд и острота взора Хаусдорфа и Мандельброта позволили увидеть, как часто фракталы встречаются в природе.

Фракталы — это не только математические объекты; они присутствуют и в окружающем мире. Слева — аэрофотосъемка норвежских фьордов, справа — фрагмент фрактала Мандельброта.

* * *