Таким образом, чтобы достичь поставленной цели, мы должны определить, какие основные свойства наделяют математические идеи эстетической ценностью. Начнем с того, что выделим два основных аспекта, внутренне присущих математическим идеям и способных перевести их в эстетическое измерение. Эти аспекты — общность и глубина.

Пример из Эйлера как отправная точка

Проиллюстрируем рассуждения Харди об этих свойствах математических идей на не слишком сложном примере, чтобы читатель, не обладающий обширными знаниями математики, мог понять его. При этом наш пример достаточно сложен, чтобы адекватно проиллюстрировать все рассуждения Харди об эстетической ценности математических идей и связать их с философскими рассуждениями об эстетике, принадлежащими другим авторам. Выбранный нами пример показывает, как Эйлер вычислил сумму чисел, обратных квадратам натуральных чисел, в своей книге «Введение в анализ бесконечно малых» (Introductio in analysin infinitorum). Эйлер вычислил следующую сумму:

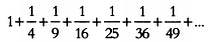
Заметьте, что знаменатели этих дробей — квадраты натуральных чисел, а многоточие означает, что число слагаемых бесконечно велико. Математики называют сумму бесконечного числа слагаемых рядом. Сумма ряда — это число, к которому мы приближаемся по мере увеличения числа слагаемых так, что разность между этим числом и суммой слагаемых уменьшается с увеличением их количества.

Представленный выше бесконечный ряд содержит некоторый контекст, о котором будет полезно рассказать.

История этого ряда такова. В марте 1672 года юный Лейбниц, которому было двадцать с небольшим, прибыл в Париж. Он хотел улучшить свое математическое образование и углубить знания, которые на тот момент были весьма скудными. Спустя несколько месяцев Лейбниц придумал хитроумный метод вычисления сумм бесконечных рядов. Его метод заключался в записи слагаемых в виде разности с последовательным сокращением членов. Ввиду врожденного оптимизма и недостатка математических знаний Лейбниц посчитал, что открытый им способ позволяет найти сумму произвольного ряда. Не будем забывать, что, по мнению Лейбница, мы жили в лучшем из миров, причем он произнес эти слова вскоре после окончания Тридцатилетней войны.

Слева — портрет Лейбница работы Иоганна Фридриха Вентцеля, около 1700 года. Справа — портрет Гюйгенса, выполненный Каспаром Нечером в 1671 году.

Оптимизм Лейбница по отношению к его методу вычисления сумм рядов только усилился, когда он узнал об открытии Христиана Гюйгенса, одного из авторитетнейших ученых. Гюйгенс родился в Голландии и к описываемому моменту уже несколько лет работал в Парижской академии наук. Чтобы проверить метод Лейбница, Гюйгенс предложил ему найти сумму ряда чисел, обратных треугольным. Треугольные числа имеют вид n·(n + 1)/2. Своим названием они обязаны пифагорейцам и их геометрическому толкованию чисел: треугольное число — это число кружков, которые можно расставить в форме равностороннего треугольника. Таким образом, Лейбницу требовалось вычислить сумму ряда: 1 + 1/3 + 1/6 + 1/10 + 1/13 + 1/21 + 1/28 + …

По случайному совпадению этот ряд — один из немногих, для которых способ, открытый Лейбницем, позволяет найти верное значение суммы (см. врезку):

1 + 1/3 + 1/6 + 1/10 + 1/13 + 1/21 + 1/28 + … = 2.

В 1673 году Лейбниц посетил Лондон, где запомнился как наивный оптимист и дилетант. С математической точки зрения его поведение не раз сослужило ему плохую службу — англичане припомнили некоторые эпизоды сорок лет спустя, в разгар дискуссии с Ньютоном об авторстве анализа бесконечно малых.

По возвращении в Париж Лейбниц получил письмо от Джона Коллинза, который предложил ему найти сумму чисел, обратных квадратам натуральных чисел:

1 + 1/4 + 1/9 + 1/16 + 1/25 + 1/36 + 1/49 + …

Коллинза нельзя было назвать великим математиком, он был скорее посредником между британскими математиками и учеными континента. Он не обладал достаточными способностями, чтобы понять истинную сложность задачи, поэтому весьма вероятно, что это предложение было выдвинуто более авторитетными математиками, к примеру Джеймсом Грегори или самим Исааком Ньютоном. Как бы то ни было, тот, кто со злым умыслом предложил Лейбницу эту задачу, мог сказать ему, что вычислить искомую сумму вряд ли будет слишком сложно, так как искомые слагаемые были почти равны членам ряда, сумму которого Лейбницу удалось найти: в одном случае слагаемые имели вид 2/(n·(n + 1)), в другом — 1/(n·n).

* * *

ВЫЧИТАЙ, КОГДА ХОЧЕШЬ СЛОЖИТЬ

Как мы уже говорили, метод Лейбница заключался в том, что при вычислении суммы ряда каждый член записывался в виде разности так, что искомую сумму было нетрудно вычислить путем последовательного сокращения членов. Именно так сокращаются числа, обратные треугольным числам. В самом деле, число, обратное треугольному числу 2/(n·(n + 1)), — это разность 2/n и 2/(n + 1):

Приняв n = 1, 2, 3, 4…, получим: 1 = 2 – 1; 1/3 = 1 – 2/3; 1/6 = 2/3 - 2/4; 1/10 = 2/4 - 2/5; 1/15 = 2/5 - 2/6; 1/21 = 2/6 - 2/7 и так далее. Сложив указанные дроби, заметим, что вычитаемое в каждой разности и уменьшаемое в следующей разности сокращаются и в конце концов остается лишь уменьшаемое первой разности: 1 + 1/3 + 1/6 + 1/10 + 1/15 + 1/21 + 1/28 + … = 2.

* * *

Однако найти сумму ряда не удалось ни Лейбницу, ни его ученикам, братьям Иоганну и Якобу Бернулли. Не сохранилось документальных свидетельств того, что этой задачей занимались Грегори или Ньютон, однако это не означает, что они обошли ее своим вниманием — возможно, их, как и других математиков, постигла неудача.

Прошло почти полвека, прежде чем Леонарду Эйлеру удалось найти сумму этого ряда. Идея, которую использовал Эйлер для сложения чисел, обратных квадратам натуральных, очень проста. Отправная точка его рассуждений такова: рассмотрим произведение вида (1 – 2z²)·(1 – 5z²)·(1 – 6z²), раскроем скобки и приведем подобные слагаемые:

(1 – 2z²)·(1 – 5z²)·(1 – 6z²) = 1 - 13z² + 52z⁴ - 60z⁶.

* * *

ЛЕОНАРД ЭЙЛЕР (1707–1783)

Эйлер был одним из величайших математиков всех времен и, вне всяких сомнений, лучшим в XVIII веке. Он родился в 1707 году в Базеле, окончил местный университет, брал частные уроки у Иоганна Бернулли — одного из учеников Лейбница.

В 1727 году он переехал в Санкт-Петербург, с 1731 по 1741 год был членом Петербургской академии наук, затем работал в Пруссии и был избран членом Берлинской академии наук. Несмотря на непростые отношения с прусским королем Фридрихом II, Эйлер прожил в Берлине 25 лет и в итоге возглавил академию наук. По словам Фридриха II, усилиями которого Берлин стал одним из культурных центров Европы, Эйлеру недоставало блеска, таланта и элегантности. Эйлер был простым человеком, лишенным качеств, необходимых для «салонной жизни», которую так любил король. В одном из писем к Вольтеру Фридрих II назвал Эйлера «огромным циклопом геометрии» — злая шутка о математике, который в 1738 году ослеп на один глаз. После Берлина Эйлер вновь вернулся в Санкт-Петербургскую академию наук и умер в Санкт-Петербурге в 1783 году.

О влиянии Эйлера на математику последующих эпох лучше всего скажет классическая фраза Лапласа: «Читайте, читайте Эйлера — он учитель всех нас!». Или процитируем Гаусса: «Изучение трудов Эйлера остается лучшей школой в различных областях математики и не может быть заменено ничем другим».

* * *

Нетрудно видеть, что число, которое умножается на z² в полученном выражении, равно сумме чисел, на которые умножается z² в левой части равенства. Также нетрудно показать, что это соотношение верно для любого числа сомножителей в этом произведении. Эйлер понял: все, что верно для конечных произведений и сумм, верно и для бесконечных. Иными словами, если мы запишем:

(1 - az²)·(1 - bz²)·(1 - cz²)·… = 1 - Az² + Bz⁴ - Cz⁶ +…,

то A = а + Ь + с + …

Далее Эйлер ввел в игру функцию синуса. Синус и косинус — две основные тригонометрические функции. Они определяются очень просто. Изобразим угол х на координатной плоскости следующим образом: одной из сторон угла будет горизонтальная ось, вторая сторона угла будет иметь длину, равную 1. Синус определяется как длина проекции этой стороны угла на вертикальную ось, косинус — как длина проекции этой стороны на горизонтальную ось, что показано на следующем рисунке.

Эйлер последовательно рассмотрел два разложения функции синуса в ряд. Один из этих бесконечных рядов открыл сам Эйлер:

где знаменатели дробей — квадраты натуральных чисел, умноженные на квадрат числа 71. Второе разложение синуса в бесконечный ряд открыл Ньютон:

Здесь знаменатели представляют собой факториалы последовательных чисел. Напомним, что факториал произвольного числа n определяется как произведение всех чисел, меньших n: n·(n — 1)·(n — 2)· … ·3·2·1. Следовательно, знаменатели в представленной выше формуле равны факториалам показателя степени z плюс 1.

Иными словами, если показатель степени z равен 2, то знаменатель будет факториалом 3: 3·2·1 = 6; если показатель степени z равен 4, то знаменатель будет равен факториалу 5: 5·4·3·2·1 = 120, и так далее.

Так как оба этих ряда представляют собой разложение одной и той же функции синуса, они должны быть равны, в частности:

Согласно изложенному в предыдущем абзаце, получим:

или, что аналогично:

Таким образом, суммой чисел, обратных квадратам натуральных чисел, будет квадрат числа π, разделенный на 6.

Размышления Харди применительно к практике

Теперь вернемся к рассуждениям Харди о двух основных свойствах, которые наделяют математическую идею эстетической ценностью. Харди писал: «Два качества играют существенную роль: общность и глубина идеи, но ни одно из них не поддается определению легко и просто».

Говоря об общности математической идеи, Харди уточнял: «Значительная математическая идея, серьезная математическая теорема должна обладать "общностью" в каком-то следующем смысле. Идея должна быть составляющей частью многих математических конструкций, используемых в доказательствах многих теорем различного рода. Теорема должна быть такой, что даже если первоначально она сформулирована в весьма частном виде (как теорема Пифагора), она должна допускать существенное обобщение и быть типичной для целого класса теорем аналогичного рода. Отношения, выявляемые в ходе ее доказательства, должны связывать многие различные математические идеи». Чтобы у читателя не осталось никаких сомнений относительно того, насколько сложно точно определить «общность», Харди писал: «Всё это очень смутно и требует многочисленных уточнений».

Рассмотрим пример, приведенный Эйлером: обладает ли ряд Эйлера общностью в том смысле, в каком трактовал это свойство Харди? Да, этот ряд действительно обладает общностью, причем в нескольких значениях.

Основная идея Эйлера заключалась в том, чтобы использовать для вычисления некоторых бесконечных сумм два представления одной и той же функции: одно в виде произведения, другое — в форме ряда. В представленном выше случае Эйлер с помощью функции синуса нашел сумму чисел, обратных квадратам натуральных чисел. Применив другие функции, Эйлер во «Введении в анализ бесконечно малых» с помощью аналогичного метода вычислил множество сумм бесконечных рядов, в частности:

В этой сумме с противоположными знаками записаны числа, обратные кубам нечетных чисел, за исключением кратных 3.

Однако общность идеи Эйлера не ограничивается одной лишь заменой функции синуса на другие. В его методе рассматривается выражение

Число, на которое последовательно умножается z², связывается с суммой чисел, на которые умножается z² в левой части равенства. В слегка видоизмененном виде идея Эйлера становится еще более плодотворной. Достаточно обратить внимание на числа, которые умножаются на остальные степени переменной в правой части равенства и выразить их через коэффициенты при z² в левой части равенства (см. врезку на следующей странице). Применив эту идею, Эйлер вычислил не только сумму чисел, обратных квадратам натуральных чисел, но и чисел, обратных четвертым, шестым и восьмым степеням:

Ему удалось дойти до 26-й степени:

Надеемся, что читатель смог оценить всю общность рассуждений Эйлера и, как следствие, лучше понять, что хотел сказать Харди, когда писал об общности математической идеи: именно общностью, помимо гениальности, отличается рассмотренная идея Эйлера.

Согласно Харди, другое неотъемлемое свойство, наделяющее математическую идею эстетической ценностью, — это глубина. «Второе свойство, которое я потребовал от значительной идеи, — ее глубина. Определить его еще труднее. Оно каким-то образом связано с трудностью; "более глубокие" идеи обычно труднее постичь, но вместе с тем это не одно и то же. Создается впечатление, что математические идеи "стратифицированы", то есть расположены как бы слоями, идеи в каждом слое связаны целым комплексом отношений между собой и с идеями, лежащими в верхних и нижних слоях. Чем ниже слой, тем глубже (и, как правило, труднее) идея».

* * *

ЭЙЛЕР И БЕСКОНЕЧНЫЕ РЯДЫ

Эйлер уточнил свою исходную идею следующим образом. Вернемся к произведению

(1 — az²)·(1 — bz²)·(1 — cz²)·… = 1 — Az² + Bz⁴ - Cz⁶ +…

Теперь рассмотрим число 8, на которое умножается z⁴. Нетрудно видеть, что это число В образуется попарным умножением с последующим сложением чисел а, Ь, с которые умножаются на z² в левой части равенства: B = ab + ac + bc + …

Таким образом, если мы запишем Р = а + Ь + с +… и Q = а² + Ь² + с² + …. путем простых подсчетов имеем: Р = A и Q = A·P — 2·B.

Если мы вновь рассмотрим два разложения для функции синуса:

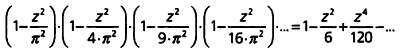
и примем во внимание, что в этом случае А = 1/6, B = 1/120 и, как мы уже вычислили, Р = π²/6, получим значение суммы чисел, обратных четвертым степеням натуральных чисел: 1 + 1/24 + 1/34 + 1/44 + … = ^π4/90.

Нечто подобное можно выполнить для z⁶ и последующих степеней. Благодаря этому Эйлер вычислил суммы чисел, обратных четным степеням натуральных чисел, начиная от второй и заканчивая двадцать шестой. Несколько лет спустя Эйлер обнаружил общую формулу суммы чисел, обратных произвольной четной степени натуральных чисел. О сумме чисел, обратных нечетным степеням натуральных чисел, ничего не известно и поныне. Мы знаем лишь, что первые несколько подобных сумм являются иррациональными числами.

* * *

И вновь суммы Эйлера помогут нам понять, что Харди имел в виду, когда говорил о «глубине» математических идей. Эйлер связал математические понятия из разных областей. В методе Эйлера скрывается понятие бесконечности, принадлежащее, можно сказать, к метафизике. Этот метод относится и к арифметике, так как в его задаче рассматриваются натуральные числа — требуется сложить квадраты чисел, обратных им. При вычислении суммы на сцену выходит геометрия, так как значение суммы выражается с помощью квадрата числа π, описывающего геометрию окружности. Наконец, весь метод Эйлера вращается вокруг представления функции в виде бесконечной суммы и бесконечного произведения — эти методы относятся к математическому анализу. И все это богатство взаимосвязей между столь разными «стратами» проявилось в одной идее Эйлера, которая на первый взгляд кажется простой. Именно это имел в виду Харди, когда говорил о глубине идеи: он рассуждал о ее способности неизбежно и плодотворно самым блестящим образом связывать между собой разные математические «страты».