А что такое эти флюксии? Скорости исчезающих приращений.
А что такое эти самые исчезающие приращения?
Они не есть ни конечные величины, ни величины бесконечно малые, но они и не нули.
Разве мы не имеем права назвать их призраками исчезнувших величин?
Епископ Джордж Беркли (1685–1753)
Процитированные выше строки взяты из памфлета «Аналитик» (The Analyst,
1734) — прекрасного интеллектуального упражнения англиканского
епископа, посвященного «одному неверующему математику» — по-видимому,
Беркли имел в виду Эдмунда Галлея (1656–1742), который славился своей недоверчивостью.
В памфлете Беркли выступает против недавно
появившегося ньютоновского исчисления, столь обожаемого Галлеем и всем
научным миром, возражая им (и небезосновательно), что если они не верят в
Бога, поскольку священные тексты им непонятны, то не следует верить и в
почти мистические хитросплетения математического анализа.
Прошли годы и даже столетия, доверие к
математическому анализу было восстановлено благодаря более строгим и
четким, но менее интуитивным определениям. Тем не менее не стоит
забывать слова Беркли, превосходного философа-эмпирика (его именем
назван знаменитый американский университет). Напротив, следует отдать
ему дань уважения за грамотную и обоснованную критику.
Методы, описанные Ньютоном и Лейбницем, открыли
множество путей в науке и вместе с тем породили множество анекдотичных
ситуаций. Приведем некоторые из них.
Портрет епископа Джорджа Беркли кисти Джона Смайберта.
Гипотезы, теоремы и Ньютон
Очевидно, что гипотеза и теорема — не одно и то же.
Гипотеза обретает статус теоремы только после доказательства, однако
довольно долго это не учитывалось.
Рассмотрим, например, труды Иоганна Кеплера (1571–1630). Все мы не раз почтительно отзывались о его законах, которые представляют собой эмпирические выводы, основанные на таблицах Тихо Браге (1546–1601).
Эти законы можно назвать гениальными, они широко известны в научном
мире и точно описывают движение небесных тел, хотя для них не приводится
какого-либо математического доказательства. Сегодня, с вершин нашего
знания, можно сказать, что это были три блестящие гипотезы, но не три
теоремы.
Лишь Исаак Ньютон (1643–1727) через 50 с
лишним лет расставил все по своим местам. Именно он, применив
элементарные законы дифференциального и интегрального исчисления к
механике, вывел три закона Кеплера исходя из фундаментальной гипотезы —
закона обратных квадратов, согласно которому два тела притягиваются друг
к другу с силой, прямо пропорциональной произведению их масс и обратно
пропорциональной квадрату расстояния между ними. Раз уж мы заговорили о
Ньютоне, который отличался особой мрачностью и неразговорчивостью, то
расскажем о нем одну историю (разумеется, апокрифическую), в которой
ученый предстает более человечным. У Ньютона была собака по кличке
Даймонд (это действительно подтверждается разными источниками), которой
он в шутку приписывал способности к математике. Как-то раз в разговоре с
Валлисом Ньютон в шутку заметил: «Сегодня до завтрака Даймонд доказал
две теоремы». Валлис подыграл ему: «Ваша собака, должно быть,
гениальна». Ньютон ответил: «Ну что вы. Одно доказательство содержало
ошибку, другое — патологический пример».
Кто платит, тот и заказывает музыку
Как-то раз в 1684 году Эдмунд Галлей, архитектор сэр Кристофер Рен (1632–1723), автор проекта собора Святого Павла в Лондоне, и Роберт Гук (1635–1703),
который первым стал использовать термин «клетка», вышли с собрания
Королевского общества, зашли в кафе и завели разговор о том, какую форму
имеет траектория планеты, притягиваемой Солнцем с силой, обратно
пропорциональной квадрату расстояния до центра масс. Рен даже согласился
выплатить денежную премию тому, кто решит эту задачу. Гук заявил, что
траекторией планеты будет эллипс, но доказательства этому не привел.
Участники встречи разошлись по домам.
Вскоре Галлей пришел к Ньютону и между делом
поинтересовался, какую же форму будет иметь траектория планеты в этой
задаче. «Эллипс», — незамедлительно ответил Ньютон. «Почему вы так
уверены в этом?» — удивился Галлей. «Потому, что я это вычислил». Галлей
наверняка подскочил от удивления — Ньютон не бросал слов на ветер.
Однако он не смог найти доказательство среди бумаг и сделал вычисления
повторно. Коротко изложим последующие события. Уступив уговорам Галлея,
Ньютон записал свои расчеты, в которых применил закон обратных
квадратов, и, слово за слово, через 18 месяцев на свет появились
«Математические начала натуральной философии» — труд, сыгравший основную
роль в формировании нашей картины мира. В нем Ньютон описал закон
всемирного тяготения, закон обратных квадратов, эллиптические орбиты
планет, а также заложил основы математического анализа. Некоторые ученые
буквально рыдали от восторга, прочтя эту полную мудрости рукопись.
Однако у Ньютона не было денег, чтобы оплатить публикацию, так что
финансировать издание книги пришлось самому Галлею. Тем более что и
родилась она отчасти благодаря его уговорам.
Галлей известен широкой публике тем, что рассчитал
орбиту кометы, названной в его честь. Эта комета появляется на звездном
небе каждые 75–76 лет, имеет видимую величину 28,2 (в 2003 году) и видна
невооруженным глазом. Ученый наблюдал комету в 1682 году и, применив
результаты наблюдений, законы механики Ньютона и собственную интуицию,
предположил, что именно ее наблюдали Петер Апиан в 1531 году и Иоганн
Кеплер в 1607 году. Если эта гипотеза верна, то, согласно расчетам
Галлея, в следующий раз комета должна появиться на небе примерно в 1758
году. В 1682 году, Галлей, высказавший свою догадку, был уже немолод, а
когда комета появилась в указанном месте точно в назначенное время, он
уже был 16 лет как мертв.
Математик и астроном Эдмунд Галлей первым рассчитал орбиту кометы, которая сегодня носит его имя.
Блистательный маркиз
Следующая история доказывает, что деньги и желание
пустить пыль в глаза часто идут рука об руку. Все началось со
швейцарской семьи Бернулли, которой мы позже посвятим несколько строк, и
с маркиза Лопиталя — Гийома Франсуа Антуана де Лопиталя, маркиза де
Сен-Мэм и графа де Антрмон (1661–1704). С маркизом произошел постыдный случай, в котором оказались замешаны члены упомянутого семейства Бернулли.
Господин маркиз был прекрасным математиком. Также он
был богат и хотел использовать деньги на благо математики и, как
язвительно замечает историк Уильям Данэм, на собственное благо, поэтому
приобрел у гениального Иоганна Бернулли права на все его открытия.
Сегодня это кажется нам возмутительным, однако в то время взгляды были
иными. Работы Иоганна Бернулли были опубликованы в 1696 году под
заглавием «Анализ бесконечно малых для познания кривых линий». По словам
Данэма, единственным, что получил маркиз в результаты сделки с
Бернулли, стала эта превосходная книга. В 1704 году, уже после смерти
Лопиталя, Бернулли рассказал подлинную историю произошедшего. Хотя
ученый и говорил правду, ему мало кто поверил: об интриганстве Бернулли
знали все, а сам он имел весьма сомнительную репутацию.
В 1921 году были найдены бумаги, подтверждающие, что
Иоганн Бернулли действительно был автором большинства открытий,
приписываемых Лопиталю, и до сих пор неясно, стремился ли маркиз к
незаслуженной славе: во-первых, Лопиталь и сам был математиком высокого
уровня, во-вторых, книга была опубликована без указания авторства, а
в-третьих, в предисловии содержится множество благодарностей Иоганну
Бернулли. Возможно, господин маркиз всего лишь хотел сделать
математическое знание доступным для всех.
Обложка первого издания самой известной книги маркиза Лопиталя.
Теперь настало время сказать несколько слов о семье Бернулли. Старшими Бернулли были братья Якоб (1654–1705) и Иоганн (1667–1748), затем историю семьи знаменитых математиков продолжили сын Иоганна, Даниил (1700–1782), и племянник братьев, Николай Бернулли (1687–1759).
На этом история семейства не заканчивается: до 1807 года в истории
науки отметились целых девять Бернулли, и все они были выдающимися
учеными. Сравниться с Бернулли талантом может разве что семья
композиторов Бахов, однако математическое семейство вошло в историю
также благодаря непростым родственным отношениям. Некоторые распри среди
Бернулли стали просто легендарными, например, ссора Иоганна с
собственным сыном Даниилом, у которого он украл часть результатов в
области гидродинамики. Вот до чего может довести зависть…
Интеграл мельника
Математики-любители вызывают определенное восхищение у
простых людей. Любители редко получают свои удивительные знания обычным
путем и часто отличаются необычными способностями, как, например,
польский математик Стефан Банах (1892–1945) или индиец
Сриниваса Рамануджан — это лишь два примера ученых, не имевших
классического образования, но занявших место на математическом Олимпе.
Однако королем среди любителей был Пьер Ферма (1601–1665) — юрист, читавший книги по арифметике, поля которых были слишком узки для его поистине чудесных доказательств.
Прекрасным примером ученого-самоучки является также Джордж Грин (1793–1841),
который совершенно самостоятельно прошел путь к математической
мудрости. Он обладал одним странным для британца качеством: в его время в
Англии считалось дурным тоном использовать в математическом анализе
нотацию Лейбница вместо нотации Ньютона. Однако Грин мало оглядывался на
общественное научное мнение и малопонятной нотации Ньютона предпочитал
способ записи Лейбница. Такая независимость его мышления удивляет еще
больше, если учесть, что он был простым мельником. Грин, сын
разбогатевшего пекаря, до 40 лет не осмеливался поступить в Кембридж, и
его насилу удалось уговорить. Именно благодаря его трудам сегодня нам
известна теорема Грина (она также независимо от него была сформулирована
русским математиком Михаилом Остроградским (1801–1861)), влияние которой прослеживается даже в современном дифференциальном и интегральном исчислении:
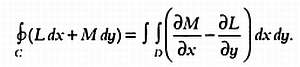
Работы Грина позднее позволили ученым добиться
значительных успехов даже в квантовой механике — науке, совершенно
немыслимой в XIX веке. Из «Небесной механики» Лапласа Грин вывел вполне
достойную математическую теорию электричества. В последние годы жизни он
часто прикладывался к бутылке. Словом, этот мельник — сегодня в его
мельнице находится музей — в обычной жизни, скорее всего, был совершенно
простым и довольно приятным человеком.
Одним из результатов практического применения теоремы Грина стало создание планиметра — прибора, позволяющего определить площадь замкнутой фигуры неправильной формы.
Мыльные пленки
Бельгийский физик Жозеф Плато (1801–1883) был
большим экспериментатором и получил множество результатов, описывающих
персистенцию зрения и принцип действия сетчатки глаза. Он же изобрел
фенакистископ. Сегодня изобретения Плато и их производные отошли в
область занимательной физики, хотя именно благодаря им стало возможным
изобретение кинематографа.
Фенакистископ стал первым прибором, в котором
использовалась персистенция — способность глаза запоминать
последовательные события. При вращении диска кажется, что фигуры
движутся.
Но как это связано с математикой? Плато почти
случайно провел эксперименты с маслянистыми жидкостями, в итоге которых
родилась теория, описывающая поверхностное натяжение и форму мыльных
пленок. Если погрузить криволинейную структуру, представляющую собой
контур поверхности (например, изогнутую проволоку), в мыльную пену, то
образуется пленка, которая будет поверхностью наименьшей площади, а
границей этой поверхности станет проволока. Именно здесь в игру вступает
математика: вычислить поверхность наименьшей площади математическими
методами — с помощью вариационного исчисления, частных производных
высших порядков и так далее — очень сложно или даже невозможно. Чтобы
найти физическое решение, достаточно воды и мыла. Таков весьма достойный
вклад Плато в математику.
Поверхность наименьшей площади, заключенная между
двумя дугами, — это не прямой цилиндр, а катеноид, что доказывает
эксперимент с мыльными пленками, изображенный на фотографии.
Жизненный путь Плато полон казусов. В 1829 году
ученый наблюдал Солнце невооруженным глазом в течение 25 секунд и ослеп.
Этот эксперимент был абсолютной глупостью, и Плато вошел в историю как
человек, принесший в жертву науке свое зрение. Согласно более
реалистичной версии, экспериментатор ослеп лишь частично, потом его
зрение восстановилось, но спустя некоторое время, в 1843 году, он вновь
начал терять зрение, в этот раз по неясным причинам, и до самой смерти
продолжал научную работу в кромешной тьме.
Открытие Нептуна
Планета Нептун была открыта в 1846 году, и это стало
триумфом математических методов вычислений. Можно сказать, что само
открытие было совершено задом наперед. Началось все с наблюдения за
Ураном — планета все время отклонялась от расчетной орбиты, и объяснить
это можно было воздействием на нее неизвестного небесного тела. В
истории об открытии Нептуна лицом к лицу сошлись английские и
французские ученые, и конфликт выплеснулся далеко за пределы Англии и
Франции — поговаривали, что уважаемые мудрецы таскали друг друга за
бороды, а серьезные журналы публиковали подстрекательские статьи.
Открытие Нептуна приписывается главе Парижской обсерватории Урбену Жану Жозефу Леверье (1811–1877) и юному английскому астроному Джону Кучу Адамсу (1819–1892).
Изначально посчитали, что именно Леверье принадлежит
честь открытия Нептуна, а все притязания Адамса — просто подозрительная
инсинуация, однако позднее историки подтвердили, что Адамс опередил
именитого французского коллегу. Ученые сделали свои открытия независимо
друг от друга, их труды были выполнены на самом высоком уровне и
содержали обширнейшие и сложнейшие расчеты.
Истории уже известен случай, когда между Англией и
Францией разгорелась бескровная война относительно того, кто же был
истинным автором математического анализа — Ньютон или Лейбниц. Спор
между Леверье и Адамсом стал повторением этого конфликта. В обоих
случаях причины для дискуссии отсутствовали, однако жаркие споры,
несомненно, куда интереснее объективных поисков истины.
Наиболее забавным эпизодом этой истории стали притязания Леверье: со слов Франсуа Араго (1786–1853),
астроном хотел назвать новую планету своим именем, о чем заявил на
заседании Французской академии наук. Не стоит и упоминать, что это
предложение было отвергнуто почти единогласно, и, как ни настаивали
французские ученые, новая планета получила имя древнегреческого бога
Нептуна. Сегодня ее символ — стилизованный трезубец.
Французская гравюра XIX века, на которой изображен астроном Адамс (слева), пытающийся подсмотреть в книгу с результатами открытий Леверье.
Здравый смысл и математика
О Томасе Эдисоне (1847–1931)
рассказывают тысячи историй, по большей части апокрифических. Однако
следующая история подтверждается сразу несколькими надежными
источниками. Один из героев этого исторического анекдота — математик из
Принстона по имени Аптон, которого Эдисон нанял для работы в своей
лаборатории. Не будем забывать, что самоучка Эдисон не получил
инженерного образования, поэтому не мог самостоятельно проводить сложные
расчеты. Как-то раз Эдисон поручил Аптону вычислить объем лампочки
грушевидной формы. Аптон, вооружившись методами интегрального
исчисления, с головой ушел в работу. Шли дни, а расчетам не было видно
конца. Эдисон потерял терпение и продемонстрировал свою гениальность —
он взял колбу от лампочки, наполнил ее водой и передал Аптону со
словами: «Измерьте объем воды, и задача будет решена».
Как важно знать ряды Тейлора
Однажды разложение функции в ряд спасло человеку жизнь. Советский физик и математик Игорь Тамм (1895–1971),
удостоенный Нобелевской премии по физике 1958 года, был не слишком
известен в бурные годы Гражданской войны, которая последовала за
Октябрьской революцией. Пытаясь немного пополнить запасы провизии, Тамм
покинул сравнительно спокойную Одессу и отправился в ее окрестности.
Однако он попал в плен к одной из многочисленных вооруженных банд, и его
посчитали переодетым коммунистическим агитатором. Дрожа от страха в
ожидании расстрела, Тамм предстал перед главарем банды. Он представился и
объяснил: я — всего лишь бедный математик, который ищет пропитание.
По лицу главаря пробежала тень сомнения. «Хорошо, —
сказал он — если ты не соврал, то мы сохраним тебе жизнь. Подсчитай-ка,
какой будет ошибка, если вместо функции f(x) мы рассмотрим ее разложение в ряд Тейлора до n-го члена».
Вопрос был не слишком трудным, и это подтвердит любой
студент-математик, однако из уст бандита, пусть даже главаря банды, он
прозвучал совершенно неожиданно. Тамм, трясясь от страха, сделал
некоторые расчеты пальцем прямо на пыльном полу. Главарь взглянул на них
и сказал: «Точно, не соврал. Что ж, иди». Больше они не встречались.
Эта абсолютно реальная история приводится в заметках Георгия Гамова.
«Простой поляк, господин учитель»
Марк Кац (1914–1984) был подлинным
светилом теории вероятностей. Мало кому известно, что по происхождению
он был поляком. По рассказам самого Каца, как-то раз он столкнулся с не
слишком способным учеником. Кац задал вопрос, как ведет себя функция
f(x) = 1/x
на поле комплексных чисел, и ученик с трудом ответил,
что это аналитическая функция (это очевидно), которая имеет критическую
точку х = 0. «А как называется эта критическая точка?» — спросил
Кац. Ученик никак не мог ответить на вопрос, и Кац сжалился над ним.
«Посмотрите на меня внимательно и скажите, кто перед вами?» Ученик
оживился: «Простой поляк, господин учитель» (на английском это звучало
как «А simple pole, sir»). Однако на языке Шекспира pole обозначает не только «поляк», но еще и «полюс».
Это и есть ответ на вопрос Каца: функция f(x) = 1/x имеет полюс в точке х = 0.
Простой полюс.
|

