Рассмотрим следующую задачу. Можно ли найти такой
путь в связном графе, который бы проходил через все вершины графа только
один раз, причем начальная и конечная вершины при этом совпадали? Такие
пути называют гамильтоновыми циклами.
На рисунке выше изображен гамильтонов цикл DABCED.
Не следует путать гамильтоновы и эйлеровы циклы: в эйлеровых циклах
нужно пройти ровно один раз по всем ребрам графа (вспомним задачу о
кёнигсбергских мостах), а в гамильтоновых циклах нужно пройти ровно один
раз по всем вершинам. Некоторые графы не содержат гамильтоновых циклов,
другие содержат сразу несколько. Например, граф, изображенный на
предыдущем рисунке, содержит два гамильтоновых цикла: DABCED и DCEBAD. Разумеется, обойти каждый гамильтонов цикл можно двумя способами: в прямом и в обратном направлении.
Несмотря на сложность поиска гамильтоновых циклов в
больших графах, эта задача представляет огромный интерес при организации
путешествий, доставке товаров, распределении продуктов в сетях
супермаркетов и так далее.
* * *
ИЗОБРЕТЕНИЕ ЦЕНОЙ В ДВЕ ГИНЕИ
Подобные циклы на графах открыл Томас Киркман (1806–1895). Исследованием этих циклов занимался ирландский математик Уильям Роуан Гамильтон (1805–1865),
он же сделал их широко известными. В 1859 году Гамильтон придумал такую
игру: 20 вершин додекаэдра (правильного 12-гранника) соответствуют 20
городам. Нужно обойти все города по одному разу и при этом вернуться в
тот же город, с которого началось путешествие. Восторженный Гамильтон
продал идею производителю игрушек за смехотворную сумму в две гинеи.
Блестящие идеи не всегда ценятся по достоинству!
Математик Уильям Роуан Гамильтон и придуманная им игра.
* * *
МЕТОД ПОСТРОЕНИЯ ДЕРЕВА
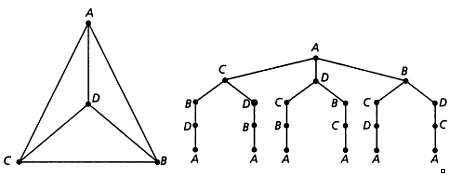
На рисунках ниже показано, как можно сопоставить исходному графу ABCD дерево всех возможных маршрутов для поиска гамильтоновых циклов, которые начинаются и заканчиваются в вершине А, а вершины В, С и D
обходятся ровно один раз. С увеличением числа вершин поиск
гамильтоновых циклов усложняется: в каждом случае исходным является
полный граф с n вершинами (им соответствует n городов). Из каждого города можно попасть в n — 1 город, из каждого из них — в n — 2 города и так далее, пока мы не вернемся в начальную точку. Следовательно, число маршрутов будет равно (n — 1)·(n — 2)·(n
— 3)·… ·3·2·1. Вспомним, что факториалом числа называется произведение
всех натуральных чисел от 1 до этого числа включительно (например, 6! =
6·5·4·3·2·1), следовательно, общее число циклов будет равно (n —
1)!. Так как каждый цикл можно пройти в прямом и обратном направлении,
то общее число различных циклов будет в два раза меньше: (n -1)1/2. Впрочем, и это число будет очень велико: для n — 6 оно составит (6–1)!/2 = 60 циклов.
 | 
