Циклы — это очень простые маршруты, проходящие через
все вершины, начальная и конечная точка которых совпадают. Примеры
циклов представлены на следующих рисунках.
Подобными графами можно представить маршруты городских автобусов или маршруты патрулей. Число вершин V равно числу ребер А.
Совокупность циклов образует так называемый
геометрический граф — плоскую фигуру из вершин (точек плоскости) и ребер
(линий, соединяющих некоторые пары вершин). Область, ограниченная
ребрами и не содержащая внутри себя вершин и ребер графа, называется
гранью. Подсчитать общее число вершин V и число ребер А несложно.
При подсчете числа граней С следует учитывать, что
внешняя часть плоскости также образует грань, так как она тоже
ограничена циклом из вершин и ребер графа. Таким образом, граф,
изображенный на следующем рисунке, имеет 10 вершин, 14 ребер и 6 граней.
Графы, в которых любая пара вершин соединена ребром,
называются полными. На следующих рисунках приведены полные графы с
числом вершин от 2 до 7. Полный граф с n вершинами обозначается Кn.
Подсчитать число ребер полного графа Кn очень просто: каждая вершина должна соединяться с n — 1 вершиной, число вершин равно n, следовательно, значение выражения n(n — 1) будет равно удвоенному числу ребер (так как каждое ребро соединяет две вершины). Поэтому общее число ребер будет равно n(n — 1)/2 — биномиальному коэффициенту 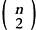 , равному числу всех возможных пар на множестве из n элементов. Зависимость между числом ребер и n является квадратичной, следовательно, число ребер Кn будет возрастать очень быстро.
* * *
ТЕОРЕМА ТУРАНА
В 1941 году Пал Туран поставил следующую задачу. Пусть дан простой граф G с n вершинами, число р(р >= 2) — число вершин полного р-вершинного подграфа графа G (иными словами, Кр). Вопрос таков: каково максимальное число ребер графа, который не содержит подобный р-вершинный подграф? Удивительно, но число ребер не может быть больше, чем n2 р/2(р -1). Эта теорема и ее очень красивое доказательство занимают важное место в теории графов.
| 
