Марен Мерсенн родился в 1388 году в скромной семье. В
16 лет он записался в Ла-Флеш — иезуитскую школу, где давали
образование детям из любых семей, вне зависимости от их достатка. В этой
школе также учился Декарт, с которым Мерсенн впоследствии поддерживал
тесные отношения. Затем он перебрался в Париж и поступил в Коллеж де
Франс, чтобы изучать философию, и в Сорбонну, чтобы постигать
богословие. Он завершил обучение в 1611 году. Решив не изменять
монашеской жизни, в июле 1611 года он записался во францисканский орден
минимов и годом позже получил сан священника. Монахи этого ордена
отличались аскетизмом, безукоризненным образованием и добродетелью.
Первые работы Мерсенна посвящены богословию, но с течением времени в нем
рос интерес к науке. Он был твердо убежден, что математика лежит в
основе всех наук и что обмен идеями является залогом прогресса в науке
вообще и в математике в частности. Ученые того времени жили в уединении,
и многие их открытия становились известны лишь спустя годы после их
смерти либо вовсе оставались в забвении. Мерсенн понял, что можно
добиться большего, если действовать сообща. Примерно в 1623 году он
начал формировать группу ученых, которые периодически собирались в его
парижской обители. На этих встречах они говорили о науке и обменивались
полученными результатами, открытиями, новыми способами вычислений. Этот
кружок дал начало Французской академии наук.
Мерсенн не ограничивался этими встречами и вел
обширную переписку со многими учеными со всего мира, создав таким
образом настоящее международное научное сообщество. Ему были известны
все современные научные достижения. Говорили, что, если он узнавал о
каком-то открытии, о нем тут же узнавал весь мир, так как Мерсенн
немедленно сообщал о нем всем, кто работал над этой темой и кому могло
быть это интересно. Перечень тех, с кем он поддерживал переписку,
огромен. В него входят Исаак Бекман, Бернар Френикль де Бесси, Чарльз
Кавендиш, Флорианус Крузиус, Жерар Дезарг, Рене Декарт, Пьер Ферма,
Галилео Галилей, Пьер Гассенди, Ян Баптиста ван Гельмонт, Томас Гоббс,
Христиан и Константин Гюйгенсы, Клод Мидорж, Этьен и Блез Паскали,
Никола-Клод Фабри де Пейреск, Джон Пелл, Жан Рей, Андре Риве, Жиль
Роберваль, Мартин Руар, Самуэль Сачиери и Эванджелиста Торричелли. После
его смерти в 1648 году в его келье были найдены письма от 78 разных
корреспондентов.
Математик и богослов Марен Мерсенн.
Помимо этого, Мерсенн много путешествовал, налаживая
контакты с растущими научными сообществами и наиболее видными учеными. В
1629–1630 годах он был в Нидерландах, в 1644 году — в Провансе и в
Италии, где познакомился с Торричелли, в 1646 году — в Бордо, где
позднее была основана Королевская академия наук. Его научные интересы
охватывали самые разные области физики и математики, и его интерес
служил путеводной нитью для заметной части научного сообщества той
эпохи. Мерсенн работал над решением задач оптики, музыки, теории тепла,
механики, гидростатики, анализа, алгебры, теории чисел и множества
других наук.
Он моментально делился соображениями с другими
учеными, которые расширяли и дополняли полученные им результаты. Таким
образом, Мерсенн никогда не работал в одиночку. Для своих коллег он был
исключительным собеседником, с которым можно было делиться идеями и
дополнять его работы.
В 1627 году Мерсенн публикует книгу «Универсальная
гармония». В предисловии к этой книге он отдает дань уважения
математическому гению Ферма. Помимо прочих вопросов, в этой книге
показывается, что частота вибрации струны пропорциональна квадратному
корню из силы натяжения и обратно пропорциональна длине струны, ее
диаметру и квадратному корню из ее массы при условии, что все прочие
переменные остаются неизменными, когда меняется значение одной из этих
величин.
Страница из книги Мерсенна «Универсальная гармония». В предисловии к этой книге автор отдает дань уважения математическому гению Ферма.
Когда Мерсенн познакомился с Христиа- ном Гюйгенсом,
он поделился с ним этими результатами. Плодом их сотрудничества стала
позднее опубликованная Гюйгенсом книга «Теория музыки». В 1646 году
Гюйгенс попытался переехать в Париж, чтобы быть ближе к своему учителю,
но ему удалось сделать это лишь спустя несколько лет после смерти
Мерсенна.
Мерсенн также интересовался идеями Галилео Галилея и
сыграл огромную роль в распространении его работ по всей Европе. 21
февраля 1632 года во Флоренции была напечатана книга «Диалог о двух
главнейших системах мира» (Dialogo sopra i due massimi sistemi del mondo) — одна из фундаментальных работ Галилея, в которой он защищал гелиоцентрическую теорию Коперника.
Это, вне всяких сомнений, всколыхнуло верхушку
католической церкви того времени, и в 1633 году Галилей предстал перед
судом и был осужден Святой палатой Римской католической церкви. В
результате книга была запрещена, но к тому времени ее копии уже
разошлись по всей Европе и с книгой успели ознакомиться многие ученые.
Среди них был Мерсенн, который был заинтригован теорией свободного
падения тел, изложенной Галилеем в этой книге. Мерсенн решил
самостоятельно провести серию экспериментов. В 1634 году он публикует
полученные результаты, которые подтвердили соотношение между ускорением
падения и квадратом времени. Он также пытался найти ответ на вопрос,
является ли изменение скорости при свободном падении непрерывным, как
считал Галилей, либо непостоянным, как утверждал Декарт.
Портрет голландского ученого Христиана Гюйгенса.
Фронтиспис книги Гэлилея Dialogo sopra i due massimi sistemi del mondo.
Переписка с Ферма
Когда Пьер де Каркави в 1636 году переехал в Париж и
объяснил Мерсенну идеи Ферма, касавшиеся теории Галилея о свободном
падении тел, Мерсенн немедленно заинтересовался мнением Ферма и написал
ему письмо. Ферма подробно ответил ему на заданные вопросы 26 апреля
того же года. Кроме этого, он сообщил Мерсенну о своей работе о
спиралях, написанной по результатам изучения траектории тел при
свободном падении, где применялись методы, описанные Архимедом в труде
«О спиралях». Ферма также рассказал о работе над восстановлением книги
«Плоские места» Аполлония. Вот что он пишет:
«Я также обнаружил множество способов анализа для
разных задач, как численных, так и геометрических, для решения которых
анализа Виета оказалось недостаточно. Я могу поделиться своими
результатами, когда вы пожелаете, и сделаю это без тени тщеславия, от
которого я свободен и далек более любого другого человека во всем мире».
Воссозданный образ Архимеда кисти Доменико Фетти, 1620 год. Ферма тщательно изучил труды этого древнегреческого ученого.
Кроме того, Ферма воспользовался моментом, чтобы
рассказать Мерсенну о двух задачах о нахождении максимумов, и попросил
его показать задачи парижским математикам. Первое же письмо дало
Мерсенну понять, кто перед ним.
С одной стороны, это яркий пример эпистолярных
отношений, существовавших в научном сообществе того времени, так как
письма были одним из основных средств обмена идеями. С другой стороны,
Ферма избегает любых проявлений нескромности. Он служит науке, а не
стремится завоевать авторитет. В письме видна его тяга к новым задачам,
которые помогали ему оценить проницательность современников. Его задачи
были вдвойне интересны благодаря тому, что Ферма знал ответы на
них. Если кому-то удавалось решить их, то возникали сомнения по поводу
авторства решения, но если найти ответ долго никому не удавалось, то
ценность найденного в итоге решения многократно возрастала — вместе со
славой его автора. Разумеется, Мерсенн с радостью передавал задачи Ферма
своим коллегам.
Задача о циклоиде
В 1632 году в Париж прибыл Жиль Роберваль, чтобы
заняться преподаванием в Коллеж де Франс. Мерсенн моментально оценил его
выдающийся талант и предложил ему решить несколько задач, на которые
сам Мерсенн не смог найти ответа. Среди них была и задача о циклоиде.
Так началась совместная работа над решением этой задачи. В 1599 году
Галилей определил циклоиду как геометрическое место точек, которое
описывает точка окружности при качении этой окружности вдоль некой
прямой.
Мерсенн был очарован красотой циклоиды и решил
заняться ее изучением. Его интересовали некоторые ее свойства: длина
дуги, описываемая площадь и так далее. Чтобы определить площадь под
аркой циклоиды, Галилей сконструировал металлическую модель и поместил
ее на весы. Так ему удалось найти приближенное значение с высокой
точностью, но этого ему показалось мало. Он хотел получить точный ответ.
Математические методы не ограничены несовершенством
модели или неточностью весов. Только с их помощью можно достичь
истинного совершенства.
* * *
ЗАДАЧА О ТАУТОХРОНЕ И БРАХИСТОХРОНЕ
Допустим, что мы хотим попасть из точки А в точку В
наиболее быстрым способом, при этом исключительно под действием силы
тяготения. Либо, что аналогично, нужно найти форму кривой, вдоль которой
мы будем скатываться, чтобы как можно быстрее попасть из точки А в точку В. Эта кривая получила название брахистохроны (от греческого брахистос — кратчайший и хронос — время). Интуиция подсказывает, что быстрейшим путем из точки А в точку В
будет кратчайший путь между ними, то есть прямая. Однако это не так.
Кривой скорейшего спуска будет перевернутая арка циклоиды, проходящая
через точку А и имеющая минимум в точке В.
В 1696 году Иоганн Бернулли нашел решение этой
задачи и предложил ее другим ученым того времени. Независимо друг от
друга ее решили Лейбниц, Ньютон, Якоб Бернулли и Лопиталь. В 1659 году
Гюйгенс обнаружил, что при свободном падении вдоль арки циклоиды предмет
окажется у ее основания в одно и то же время вне зависимости от высоты,
с которой началось падение. Следовательно, циклоида также является
решением задачи о таутохроне (от греческого тауго — равный и хронос — время).
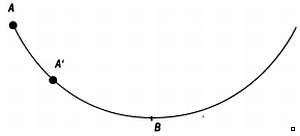 При свободном падении как из точки А, так и из точки А' предмет достигнет точки В за одно и то же время.
* * *
Мерсенн посвятил изучению циклоиды много лет. Он
опубликовал результаты в различных трудах: «Известные вопросы Книги
Бытия» (1623), «Синопсис математики» (1626) и «Вопросы теологии, физики,
морали и математики» (1634). Как и всегда, в письмах он сообщал
полученные результаты и вопросы, на которые ему удалось найти ответы.
Торричелли, Ферма, Декарт, Роберваль верно вычислили, что площадь под
аркой циклоиды равна утроенной площади порождающего круга циклоиды.
Роберваль и Рен определили, что длина арки в восемь раз превышает ее
радиус. Какие красивые ответы на столь простые вопросы! И сколько
вычислений потребовалось, чтобы найти эти несложные на вид ответы!
Благодаря новой организации работы, предложенной
Мерсенном, к решению интересных задач приглашались все талантливые
ученые. Найденные решения были не плодами труда одиночек-затворников, а,
напротив, результатом взаимодействия и обмена идеями. История науки
знает множество примеров, когда формулы и теории получали имя своих
первооткрывателей. Но в этой новой среде достижения часто были
результатом коллективного труда. Кто мог представить, что эта красивая
кривая, которую впервые описал Галилей как движение точки окружности при
качении вдоль прямой, спустя много лет окажется решением задачи о
брахистохроне и таутохроне, и что Жерар Дезарг предложит придать зубцам
часовых механизмов именно форму циклоиды!
Понте ди Меццо в Пизе, спроектированный учениками Галилея. Его арки имеют форму циклоиды. Мост был разрушен в 1944 году.
|

