Мерсенн узнал об этом и написал Ферма, попросив сохранять осмотрительность и сообщить свое мнение только ему и никому больше. 22 сентября 1637 года Ферма пишет Мерсенну: «Вы спрашиваете мое мнение о труде о диоптрии сеньора Декарта. Мое впечатление о его предложениях таково: хотя выводы, к которым он приходит, когда говорит о форме линз, изящны, было бы желательно, чтобы основы, на которых строятся его выводы, были доказаны лучше, так как сейчас этого не сделано. Но боюсь, что в его работе истина отсутствует в той же мере, что и доказательство». В этом же письме Ферма объясняет свое мнение. В «Диоптрике» предлагается модель света, объясняющая закон преломления. Но эта модель основана на предпосылках, которые показались Ферма не совсем обоснованными. Ферма заметил противоречие между тем, что свет распространяется мгновенно, и тем, что скорость света зависит от среды, где он распространяется. Ему также было неясно, почему свет быстрее распространяется в более плотной среде.

Мерсенн передал Декарту мнение Ферма, и, как вы можете себе представить, оно совершенно не понравилось Декарту. Так, в октябре 1637 года он отвечает Мерсенну: «Ошибка, которую нашел сеньор Ферма в моем доказательстве (о преломлении света), является надуманной и свидетельствует о том, что он ознакомился с моим трудом лишь мимоходом».

Обложка знаменитого «Рассуждения о методе» Декарта, куда вошел очерк о природе света, вызвавший споры с Ферма.

Но Ферма интересовала не полемика, а поиск истины. В письме к Мерсенну в декабре 1637 года он предлагает новую модель преломления света. В этом же послании он пишет: «…Я продолжаю этот небольшой диспут не ради зависти или жажды соперничества, но желаю лишь того, чтобы воссияла истина. Это, разумеется, доставит удовольствие сеньору Декарту, столь известному благодаря своим заслугам, которым я выражаю здесь свое почтение».

Но спор уже начался. Декарт воспринял мнение Ферма как вызов своим идеям и себе лично. «Рассуждение о методе» и три эссе составляли фундамент его философии и основу его мысли. Поэтому он решил подготовиться к сражению по всем правилам. 18 января 1638 года он пишет Мерсенну: «Если этого автора удивляет отсутствие некоторых правил в моей геометрии, я имею куда больше причин удивиться тому, что он пожелал начать бой, не приготовив оружия. Ноя хочу дать ему время снова взобраться на коня и подобрать наилучшее оружие для этого сражения».

Когда Ферма отправил на рассмотрение парижских математиков свой труд «Методы нахождения максимумов и минимумов и построения касательных к кривым», Декарт нашел возможность отыграться и объявил рассуждения Ферма сомнительными. Роберваль и Этьен Паскаль встали на его защиту, а Мидорж и Дезарг приняли сторону Декарта. В апреле 1638 года Роберваль пишет: «Когда сеньор Декарт всецело поймет метод максимумов и минимумов и построения касательных к кривым сеньора Ферма, то оставит сомнения в том, почему этот метод нашел своих сторонников, и оценит по достоинству этот превосходный метод, достойный своего автора». Любопытную роль в этой истории сыграл Мерсенн, так как вся переписка велась через него. Декарт, равно как и Ферма, отправлял письма Мерсенну, подразумевая, что он объяснит их содержание противоположной стороне. В итоге Дезарг признал правоту Ферма, и Декарту пришлось принять очевидное: «Увидев последний метод, примененный для нахождения касательных к кривым, я не могу ответить иначе как признав, что он очень хорош и что если бы он был объяснен в такой форме с самого начала, то я абсолютно не стал бы противоречить».

Страсти постепенно улеглись. 29 июня 1638 года Декарт пишет Мерсенну: «Я вижу, что вы оказали любезность сообщить мне о письмах Ферма в мой адрес, прежде всего относящихся к тому, что он сказал, что его чрезвычайно огорчили слова моей первой статьи. Я смиренно прошу у него прощения за высказанные упреки».

Наконец, в октябре 1638 года Декарт впервые пишет самому Ферма в знак примирения: «Должен признаться, что я никогда не встречал никого, кто производил бы впечатление человека, столь сведущего в геометрии, как вы… Несмотря на это, подобно тому как наш взгляд более пристально задерживается на малейших изъянах бриллианта, чем на крупных огрехах простого камня, так и я посчитал нужным более пристально рассмотреть ваши слова по сравнению со словами любого другого человека, которого я ценил бы не столь высоко».

Но инцидент этим не исчерпался. Декарт видел в Ферма гения и соперника, поэтому побаивался его и старался подорвать его авторитет при любой возможности. Как-то раз, проанализировав работу Ферма об определении касательной к циклоиде (работа не содержала ошибок), Декарт написал Мерсенну, что в труд Ферма вкрались ошибки и Ферма не соответствует званию математика и мыслителя. Декарт занимал заметное положение в научном сообществе того времени, и это, несомненно, повлияло на то, что у многих ученых сложилось ошибочное представление о Ферма.

Но гений Ферма не переставал сверкать. Он первым заложил основы алгебраической геометрии, опередив Декарта с его «Геометрией». Вместе с Паскалем он создал теорию вероятностей. Достигнутые им результаты в алгебре и методы доказательства, которые он использовал, дали начало современной теории чисел. Его вклад в математику этим не ограничивается — мы привели лишь несколько примеров. Наконец, Ферма как математик несомненно превзошел Декарта. Ферма всячески старался сгладить трения и остроумно заметил, комментируя ошибку в «Геометрии», что так ценит гений Декарта, что, несмотря на все имеющиеся ошибки, эта работа достойнее других, в которых нет ни единой неточности.

Теория преломления света

История имела продолжение, когда речь зашла о теории преломления света. После смерти Декарта один из учеников предложил опубликовать все его письма. Он обратился за помощью к Ферма, попросив у того все письма, полученные от Декарта. Это побудило Ферма пересмотреть свою работу о преломлении света. Он остался недоволен своими же рассуждениями и решил заняться этой темой повторно. Именно тогда он сформулировал принцип, согласно которому свет распространяется по траектории, для которой время движения минимально. Этот принцип теперь известен как принцип Ферма. Он был включен в труд «Анализ и синтез преломления лучей», опубликованный примерно в 1660 году. С помощью этого принципа стало возможным дать математическое объяснение закону Снелла. И опять мы видим, с каким упорством Ферма подходил к решению задач. Он возвращался к ним снова и снова, всякий раз совершая новые открытия. Такого же упорства он ждал и от своих современников при решении задач, которые предлагал им.

* * *

ЗАКОН СНЕЛЛА

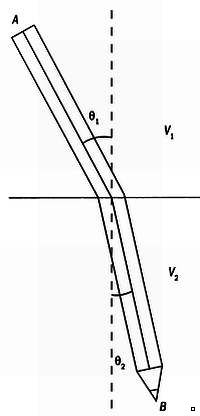
Если погрузить палочку в воду, то кажется, будто она сломана пополам и что угол наклона в воде и в воздухе отличается. Это оптическое явление, называемое преломлением, происходит из-за того, что скорость света меняется в зависимости от плотности среды, в которой он распространяется. Плотность воздуха меньше, чем воды, и скорость света в воздухе выше, чем в воде, так как в воздухе свет встречает меньше «препятствий» на своем пути.

Виллеброрд Снелл открыл формулу, известную как закон Снелла, которая связывает скорости света в двух средах и углы преломления:

sin θ₁/V₁ = sin θ₂/V₂

Принцип Ферма дает математическое объяснение этому явлению. Согласно этому принципу, свет распространяется по траектории, для которой время движения минимально. Допустим, что, как показано на рисунке, птица хочет попасть из точки А (конец палочки, расположенный над водой) в точку В (конец палочки, погруженный в воду).

Предположим, что птица летит в воздухе со скоростью v₁ а под водой плывет со скоростью v₂. Ферма доказал, что кратчайшим путем из точки А в точку В является не прямая, а линия, повторяющая изгиб палочки. Значит, птица должна следовать вдоль палочки, чтобы как можно скорее попасть в точку В.