"Морской бой” — излюбленная игра, как младших,
так и старших школьников.
Главная цель — "потопить” 10 кораблей
противника путем прямого попадания в корабль.
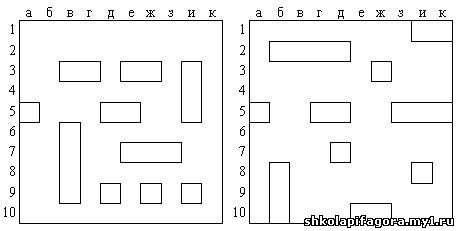
Игровое поле представляет собой квадрат,
состоящий из 10 строк, обозначенных числами от 1 до
10 и 10 столбцов, обозначенных буквами от А до К, а
значит, состоит из 100 клеток. Координаты цели
определяются именем столбца и строки.
В предложенном варианте "Морского боя”
правила несколько изменены. Играть могут 4-
команды. Игровое поле — квадрат — один для всех
команд. Он находится на видном месте и имеет
большие размеры. На игровом поле размещены
корабли.
Участникам необходимо "овладеть” всеми
кораблями.
По очереди команды делают "выстрелы”,
указывая координаты на игровом поле.
Если произошло попадание в одну из палуб, то
команде сразу начисляется 1 очко и дается право
на следующий выстрел. Если попадания не
произошло, то команда получает задание. В случае
правильного ответа команда получает одно очко и
право на следующий выстрел. В случае
неправильного ответа команда очко не получает и
право "выстрела” переходит к другой команде.
Игра завершается после того, как участники
"овладели” всеми кораблями.
Победителем становится команда, набравшая
наибольшее количество очков. Итог состоит из
очков, набранных за правильные ответы и
премиальных очков, полученных за "овладение”
каждым кораблем.
На столе у каждой команды находятся наборы
вопросов, пронумерованные в соответствии с
расположением кораблей на игровом поле.
Данную игру можно провести, как итоговое
повторение по теме: "Квадратные уравнения и
уравнения, приводящиеся к квадратным,
рациональные уравнения”.
А.1 Упростить выражение:
а) 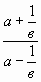 ; б) ; б)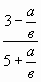 . .
А.2 Выполнить действия:
а)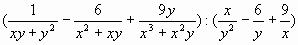 ; ;
б)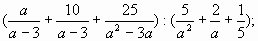
А.3 Решить задачи:
а) Периметр земельного участка прямоугольной
формы равен 60 м, а его площадь 200м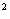 . Найти размеры участка. . Найти размеры участка.
б) Длина земельного участка прямоугольной
формы на 20 м. больше его ширины, а площадь 800 м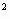 . Найти размеры
участка. . Найти размеры
участка.
А.4 Решить уравнение:
а)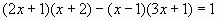 ; ;
б)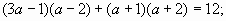
А.5 Решить уравнение:
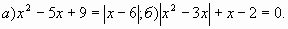
А.6 Сократить дробь:
а)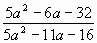 ; б) ; б)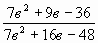 . .
А.7 Решить дробное рациональное уравнение:
а)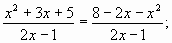
б)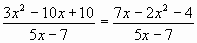 . .
А.8 Решить задачи:
а) Женя шёл по лесной дорожке к станции, но, не
дойдя до неё 4 км, он сделал привал на 20 мин. для
сбора грибов. Чтобы успеть на электричку ему
пришлось увеличить скорость на 1 км/ч. С какой
скоростью шёл Женя первоначально?
б) Дима шёл вдоль реки к остановке автобуса. Не
дойдя 3 км. до остановки, он решил искупаться и
потратил на это 15 мин. Чтобы успеть на автобус, он
увеличил скорость на 2 км/ч. С какой скоростью шёл
мальчик?
А.9 Решить систему уравнений:
а)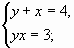 б) б)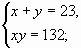
А.10 Решить уравнение:
а)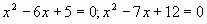 ; ;
б)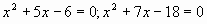 . .
Б.1 При каких значениях р имеют общий корень
уравнения: 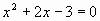 и и

Б.2 Решить уравнение:
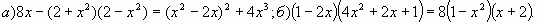
Б.3 Решить задачи:
а) Сумма квадратов трёх последовательных чисел
равна 365. Найти эти числа.
б) Найти три последовательных чётных числа,
чтобы сумма квадратов первых двух равнялась
квадрату третьего числа.
Б.4 Выполнить действия:
а)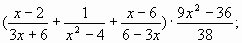
б) 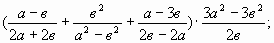
Б.5 Не решая уравнения 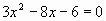 найти: найти: 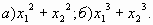
Б.6 Решить дробное рациональное уравнение:
а)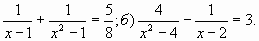
Б.7 Решить задачи:
а) Через первую соковыжималку можно
приготовить сок на 1час быстрее, чем через вторую.
А через вторую на 3 часа быстрее, чем через третью.
За какое время можно приготовить сок, пользуясь
первой, если это время равно времени, за которое
можно приготовить сок, пользуясь вместе второй и
третьей?
б) через первую трубу можно наполнить бассейн
на 5 часов быстрее, чем через вторую, а третья
труба наполняет бассейн на 4 часа быстрее, чем
первая. За какое время можно наполнить бассейн
через третью трубу, если это время равно времени,
за которое наполняют бассейн первая и вторая
труба вместе?
Б.8 Дано равенство 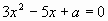 . Выразить а через в. . Выразить а через в.
Б.9 При каких значениях а один из корней
уравнения 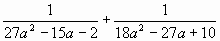 равен 2? Для данного значения а найти другие корни
уравнения.
равен 2? Для данного значения а найти другие корни
уравнения.
Б.10 Сложить дроби:
а) 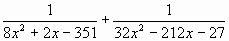 ; ;
б)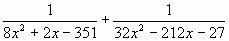 . .
В.1 При каких значениях параметра р корни 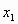 и и 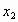 уравнения удовлетворяли
условию ? уравнения удовлетворяли
условию ?
В.2 Решить уравнение:
 а) а)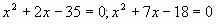 ; ; б) б)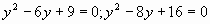 . .
В.3 При каких значениях с уравнение 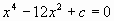 не имеет
корней? не имеет
корней?
В.4 Решить задачи:
а) Скорость мотоциклиста на 40 км/ч больше
скорости велосипедиста. Поэтому на весь путь 30 км
мотоциклист затратил на 1 час меньше, чем
велосипедист. Сколько на этот путь тратит
велосипедист?
б) Скорость велосипедиста на 6 км/ч больше
скорости пешехода. Весь путь 18 км велосипедист
проехал на 1,5 часа меньше, чем пешеход. Сколько
времени потратит пешеход?
В.5 Решить систему уравнений:
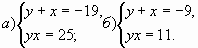
В.6 Решить уравнение:
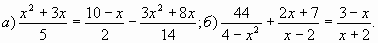
В.7 Дано равенство 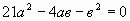 . Выразить а через в. . Выразить а через в.
В.8 Решить задачи:
а) Двое рабочих могут выполнить работу за 12
дней. После 8 дней совместной работы первый
рабочий перешёл на другой участок. Второй
окончил её за 5 дней. За сколько дней каждый из
них, работая отдельно, может выполнить эту
работу?
б) Баржа была разгружена с помощью двух кранов в
течение 15 часов, причём первый кран приступил к
работе на 7 часов позже второго. Известно, что
первый кран, работая отдельно, может разгрузить
баржу на 5 часов быстрее, чем второй. За сколько
часов может разгрузить баржу каждый кран,
работая отдельно?
В.9 Решить уравнение:
а)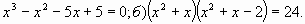
В.10 Решить уравнение:
а)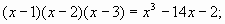 б) б) 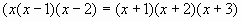 . .
Г.1 Найти меньший корень.
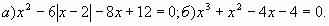
Г.2 При каких значениях параметра р корни 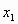 и и 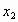 уравнения уравнения 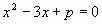 удовлетворяли условию удовлетворяли условию 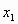 - - 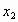 = 7? = 7?
Г.3 Найти сумму корней.
 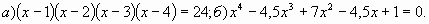
Г.4 Сократить дробь:
а) 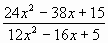 ; б) ; б)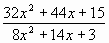 . .
Г.5 Решить задачи:
а) От города до турбазы туристы шли на байдарке
и прошли 16 км. Вернулись обратно на автобусе по
шоссе, проехав 20 км. Скорость автобуса на 22 км/ч
больше скорости байдарки. Найти скорость
автобуса, если на обратный путь затрачено на 1 час
20 мин меньше.
б) До озера рыбак добирался по дороге на
грузовике и проехал 10 км. Обратно шёл через поле 5
км. Найти скорость рыбака, если она на 15 км/ч
меньше скорости грузовика и на обратный путь он
затратил на 30 мин больше, чем на путь до озера.
Г.6 Дано равенство 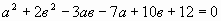 . Выразить в через а. . Выразить в через а.
Г.7 Решить уравнение:
а) 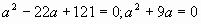 ; б) ; б) 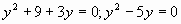 . .
Г.8 При каких значениях а уравнения 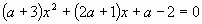 и и 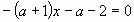 равносильны? равносильны?
Г.9 Решить дробное рациональное уравнение:
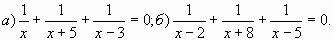
Г.10 Решить задачи:
а) Две бригады трактористов, работая вместе,
могут вспахать поле за 3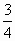 ч. Работая порознь, первая бригада
вспахивает поле на 4 часа быстрее второй. За
сколько часов могут вспахать поле первая и
вторая бригады, работая отдельно? ч. Работая порознь, первая бригада
вспахивает поле на 4 часа быстрее второй. За
сколько часов могут вспахать поле первая и
вторая бригады, работая отдельно?
б) Две сенокосилки, работая вместе, могут убрать
урожай за 7,5 ч. А, работая порознь, первая убирает
на 8 часов быстрее второй. За сколько часов могут
по отдельности убрать урожай каждая сенокосилка?
Д.1 Решить уравнение:
а)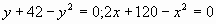
б)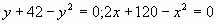 . .
Д.2 При каких значениях с один из корней
уравнения 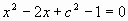 равен нулю?
равен нулю?
Д.3 При каких значениях к уравнение 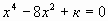 не имеет
корней? не имеет
корней?
Д.4 Решить задачи:
а) Две бригады столяров делали стулья. Первая –
65, вторая – 66. Первая бригада делала за 1 день на 2
стула больше, но работала на 1 день меньше, чем
вторая. Сколько стульев за 1 день делали две
бригады вместе?
Д.5 Дано равенство 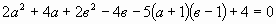 . Выразить в через а. . Выразить в через а.
Д.6 Решить уравнение:
а)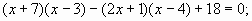
б)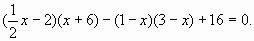
Д.7 Решить систему уравнений:
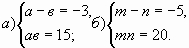
Д.8 Решить задачи:
а) Два комбайна могут собрать урожай с поля на 9
дней быстрее, чем один первый комбайн, и на 4 дня
быстрее, чем один второй. За сколько дней каждый
комбайн может собрать урожай?
б) Для наполнения бассейна через первую трубу
потребуется времени на 9 часов больше, чем для
наполнения через первую и вторую трубы
одновременно, и на 7 часов меньше, чем через одну
вторую трубу. За сколько часов наполнится
бассейн через обе трубы?
Д.9 При каких значениях параметра р корни 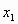 и и 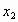 уравнения уравнения  удовлетворяли условию удовлетворяли условию 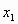 - - 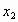 = -6? = -6?
Д.10 Решить дробное рациональное уравнение:
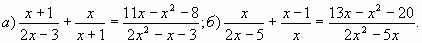
| 
