ХОД УРОКА. 1. Организационный момент Задачи, в которых встречается деление многочленов, играют огромную роль в формировании логического мышления и математической культуры. Решение таких задач весьма полезно еще и потому, что они раньше встречались на вступительных экзаменах во многих престижных вузах, а сейчас это – задания из части С ЕГЭ. На первом уроке – повторение и обобщение материала по данной теме и контроль усвоения при помощи теста. На втором уроке рассматривается следствие из теоремы по поиску рациональных ненулевых корней многочлена, которая была изучена на прошлом уроке. Далее надо научиться применять это следствие при решении уравнений. Завершается урок самостоятельной работой обучающего характера. 2. Проверка домашнего задания №2.50(в), №57(б,г) с.332 учебник С.М.Никольского «Алгебра и начала анализа»/ Вызвать двух учеников к доске – подготовить решение домашних задач. Дополнительные вопросы: №2.50. В данной задаче нам легко удалось разложить найденный многочлен на множители, поскольку был известен корень многочлена 4. Если бы этого не было, то как надо было бы поступить? Среди каких рациональных чисел можно искать корни данного многочлена? №57(б, г) с. 332 Сформулируй теорему по поиску рациональных корне многочлена. (Пусть коэффициенты многочлена Рn(х) – целые числа и 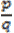 – рациональный корень причем, дробь – рациональный корень причем, дробь 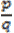 несократима. Тогда свободый член а0 делится на p, а старший коэффициент делится на q) несократима. Тогда свободый член а0 делится на p, а старший коэффициент делится на q) 3. Устный опрос 1. Что называется многочленом от одной переменной? (Многочлен вида Р(х) = …. наз. многочленом от одной переменной. Этот вид многочлена наз. каноническим.) 2. Как определить степень многочлена? Имеет ли степень нулевой многочлен? (Сначала многочлен приводим к каноническому виду. Если аn=/= 0, то число n называется степенью многочлена. Степень нулевого многочлена не определяется). 3. Определите степени следующих многочленов: 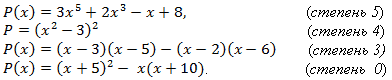
4. Что значит – разделить с остатком многочлен А на ненулевой многочлен В? (Разделить с остатком многочлен А на неявляющийся нулевым многочлен В – значит представить его в виде A = Q . B + R, где Q, R – некоторые многочлены, причем степень R меньше Q.) 5. Расскажите про алгоритм, который носит название схемы Горнера на следующем примере: 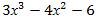 на х – 2. (Схема Горнера применяется при делении многочлена на двучлен на х – 2. (Схема Горнера применяется при делении многочлена на двучлен 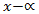 . Начертим таблицу, состоящую из двух строк и n + 1 столбцов. В нашем случае – это 2 строки и 4 столбца. В первой строке запишем все коэффициенты многочлена, рядом с нижней строкой – число 2. В нижней строке получатся все коэффициенты частного и остаток.) . Начертим таблицу, состоящую из двух строк и n + 1 столбцов. В нашем случае – это 2 строки и 4 столбца. В первой строке запишем все коэффициенты многочлена, рядом с нижней строкой – число 2. В нижней строке получатся все коэффициенты частного и остаток.) 6. Как читается теорема Безу? (Остаток от деления многочлена 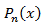 на двучлен на двучлен 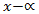 равен равен 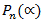 ) ) 7. Найдите остаток от деления многочлена 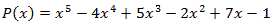 на двучлен на двучлен 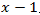 . (R = P(1) = 1 – 4 + 5 – 2 + 7 – 1 = 6, остаток равен 6). . (R = P(1) = 1 – 4 + 5 – 2 + 7 – 1 = 6, остаток равен 6). 8. Сформулируйте следствие из теоремы Безу. (Для того, чтобы многочлен 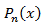 делился на делился на 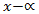 , необходимо и достаточно, чтобы , необходимо и достаточно, чтобы 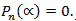 ) ) 9. Делится ли многочлен 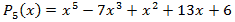 на на 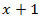 нацело? ( нацело? (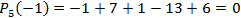 , значит, многочлен делится на двучлен нацело) , значит, многочлен делится на двучлен нацело) 10. Что называют корнем многочлена Рn(х)? (Число х0 называют корнем многочлена Р(х), если Р(х0) = 0.) 11. Определите, является ли число а) 0; б) 1 корнем многочлена 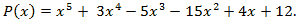 (P(0) = 12, P(1) = 0) (P(0) = 12, P(1) = 0) 10. Сформулируйте теорему по поиску рациональных ненулевых корней многочлена. (Пусть коэффициенты многочлена Рn(х) – целые числа и 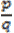 – рациональный корень, причем, дробь – рациональный корень, причем, дробь 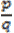 несократима. Тогда свободый член а0 делится на p, а старший коэффициент делится на q) несократима. Тогда свободый член а0 делится на p, а старший коэффициент делится на q) 4. Подведение итогов первой половины урока 5. Тест 6. Ответы к заданиям теста 7. Проверка выполнения теста В результате выполнения заданий В1, В2, В3 теста и получения верных ответов на доске появится запись «МОЛОДЦЫ УМНИЦЫ 11 Б» 8. Подведение итогов урока
| 
