Цели урока:
- Обобщение и систематизация теоретического
материала по данной теме;
- Отработка умения и навыков применения и свойств
арифметической прогрессии при решении задач;
- Развитие навыков работы с дополнительной
литературой, электронным учебником и
историческим материалом;
- Развитие познавательной активности учащихся;
- Формирование интереса к изучению математики;
Оборудование:
- компьютер,
- проектор,
- тесты,
- дополнительная литература - сборники ЕГЭ
(Кузнецова Л.В., Цыганова Ш.И.),
- электронный учебник.
Ход урока
Орг. момент: Приветствие учащихся.
Сообщается тема план и цели урока.
1. Урок начинается с исторической справки.
Учитель рассказывает о "Арифметической
прогрессии в древности"
Арифметические прогрессии в древности.
В клинописных табличках вавилонян, в
египетских пирамидах (ll в. до н.э.) встречаются
примеры геометрических прогрессий. Вот пример
задачи из египетского папируса Ахимеса:
"Пусть тебе сказано: раздели 10 мер ячменя между
10 человеками, разность же между каждым человеком
и его соседом равна 1/8 меры.
Вот формула, которой пользовались египтяне:
a= S/n - (n-1) d/2 (S= (a+b) n/2 )
Задачи на прогрессии, дошедшие до нас из
древности, были связаны с запросами
хозяйственной жизни: распределение продуктов,
деление наследства и др. Некоторые формулы,
относящиеся к прогрессиям, были известны
китайским и индийским ученым.
Ариабхатта (V в.) применял формулы общего числа,
суммы арифметической прогрессии. Но правило для
нахождения суммы членов произвольной
арифметической прогрессии впервые встречается в
сочинении "Книги абака" в 1202 г. (Леонардо
Пизанский).
2. Проверка домашнего задания.
На откидных досках выполняют два ученика
упражнения заданные на дом. Решение проверяются
после устного опроса. Учащиеся оцениваются.
3. Устная работа
Фронтальный опрос:
Определение арифметической прогрессии.
Примеры.
Разность арифметической прогрессии. ( 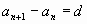 ) )
Дано: 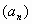 - арифметическая прогрессия, - арифметическая прогрессия, 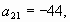 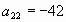 . Найти: d (2) . Найти: d (2)
Рекуррентная формула арифметической
прогрессии. (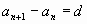 ) )
Формула n-го члена арифметической прогрессии. (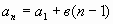 ) )
Дано: 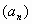 - арифметическая прогрессия, - арифметическая прогрессия, 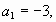 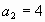 . Найти: . Найти: 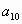 (60) (60)
Характеристические свойства арифметической
прогрессии.
(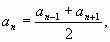 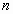 >1 - среднее
арифметическое) >1 - среднее
арифметическое)
Дано: 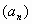 - арифметическая прогрессия, - арифметическая прогрессия, 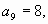 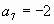 . Найти: . Найти: 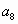 и d (3, d=5) и d (3, d=5)
Формула суммы n-членов конечной арифметической
прогрессии
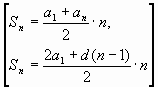
Найдите сумму членов конечной арифметической
прогрессии, 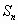 если: если: 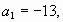 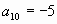 , (-90) , (-90)
4. Решение задач
а) Устный разбор задачи №14 (тест 5) из первой
части стр.27
Идет устный разбор решения задачи, один ученик
оформляет на доске, остальные в тетрадях.
№14. В арифметической прогрессии 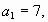 d=5. Выяснить, содержится ли в этой
прогрессии число 132 и если да, то найдите его
номер. d=5. Выяснить, содержится ли в этой
прогрессии число 132 и если да, то найдите его
номер.
Решение: проверка
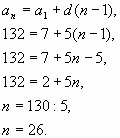
Ответ: да.
б) Разбор более сложной задачи №3 на доске (тест
7) из второй части стр.38. Задача разбирается устно.
Один ученик работает у доски.
№3 Вася выписывает последовательно четные
натуральные числа, начиная с 2. Олег, увидев
очередное число, подсчитывает сумму всех
выписанных к этому моменту чисел и получает
ответ 306. Какое число увидел Олег?
Решение: проверка
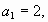 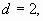
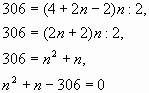
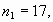 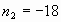 не принадлежит
множеству N не принадлежит
множеству N
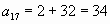
Ответ: 34.
Физминутка
Физорг класса в течение 2 минут ведет
физические упражнения.
Решение задач с электронного учебника.
Электронный учебник. (Алгебра 7-11).
№1 а) Упражнение на нахождение членов
арифметической прогрессии:
Найти 28 член арифметической прогрессии (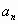 ), если ), если 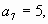 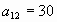 . .
Прочитав условие задачи, учащиеся выясняют, что
задачу можно решить двумя способами. Два ученика
решают у доски. Решением учащиеся сверяются с
электронного учебника.
Решение: проверка
1-й способ.
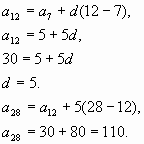
Решение: проверка
2-й способ.
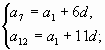
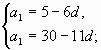
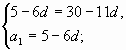
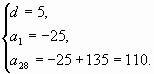
Ответ:110
№2 б) Геометрическая задача
(Разбор задачи вместе с учащимися, один ученик
оформляет на доске, с решением сверяемся по
электронному учебнику через видеопроектор на
экране.)
Длина сторон прямоугольного треугольника три
последовательных члена возрастающей
арифметической прогрессии. Найдите разность
этой прогрессии, если его периметр равен 120.
Решение: проверка
Пусть разность прогрессии равна d, d больше нуля.
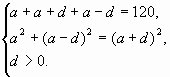
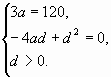
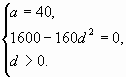
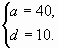
Ответ: d=10
Самостоятельная работа.
(Сборник тестов 7-9 А.Г. Мордкович)
Решив задание, учащиеся делают взаимопроверку
с соседом по парте.
Ключ к тестам и критерий оценок на откидной
доске.
1 Вариант
1) Найдите четвертый член арифметической
прогрессии: 13, 9, :
А. 0. Б. 6. В. -1. Г. 1.
2) Дана арифметическая прогрессия -3,5; -2; :
найдите номер члена этой прогрессии, равного 59,5.
А. 44. Б. 43. В. 34. Г. Нет такого номера.
3) Найдите сумму первых 16 членов арифметической
прогрессии, заданной формулой 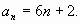
А. 864. Б.848. В. 792. Г. 716.
4) Сумма второго и третьего членов
арифметической прогрессии равна 16, а разность
прогрессии равна 4. найдите первый член
прогрессии.
А. 2. Б. 4. В. 5. Г. 6.
2 Вариант
1) Найдите первый член арифметической
прогрессии: 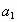 , , 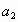 , 4, 8, : , 4, 8, :
А. 1. Б. 12. В. -4. Г. -1.
2) Дана арифметическая прогрессия 8,2; 6,6; :
Найдите номер члена этой прогрессии, равного -15,8.
А. 16. Б. 14. В. 17. Г. Нет такого номера.
3) Найдите сумму первых 14 членов арифметической
прогрессии, заданной формулой 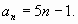
А. 511. Б. 497. В. 1022. Г. 1400.
4) Третий член арифметической прогрессии равен
6, а пятый равен 10. Найдите первый член
арифметической прогрессии.
А. 1. Б. 2. В. -1. Г. 0.
Ключ к тестам:
1 Вариант (ГББА)
2 Вариант (ВААБ)
Задание на дом.
По сборнику Ш.И. Цыганова: 1) стр. 43 В-8, 2) стр. 46 В-7
Итог урока.
- Оценивание учащихся.
- Выводы.
Учащиеся отвечают на вопрос: Что нового
получили на уроке?
| 
