Определение модуля
Алгебрагическое определение: | x |
= 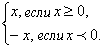
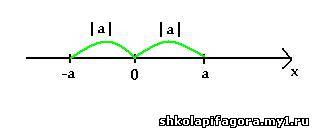
Геометрическое определение: модулем
числа называется расстояние от точки,
изображающей это число, до начала отсчета.
Понятие модуля впервые вводится в 6 классе, в 7
классе рассматривается линейная функция и ее
график и уже можно показывать построение
несложных графиков функций, содержащих модуль.
Далее, по мере изучения различных функций, их
свойств, каждую такую тему можно заканчивать
рассмотрением более сложных графиков, в том
числе с модулем. В этой статье рассматриваются
основные приемы построения графиков таких
функций.
I. На алгебрагическом определении основан метод
«раскрытия модуля на промежутках».
Например: | x + 2 | = 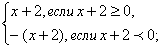 | x + 2 | = | x + 2 | = 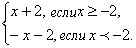
Этот
метод можно применять при построении графиков
функций, содержащих один или более модулей.
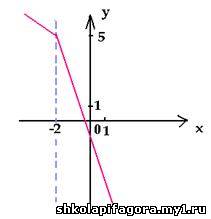
Например, построим график функции у = | x + 2 | –
2x + 1 , предварительно упростив ее.
у = 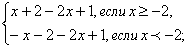 у
= у
= 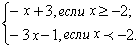
Если модулей несколько, то каждый из них
раскрываем на промежутках относительно точек,
обращающих каждый из них в нуль. Например,
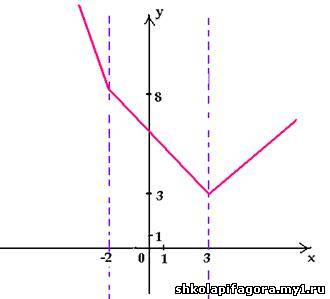
построим график функции у = | 3 – x | – x
+ | x + 2 | + 1.
1. Если х < – 2, то у = 3 – х – х
– (х + 2) + 1, у = – 3х + 2.
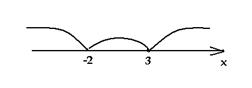
2. Если –2
< х < 3, то у = 3 – х – х + х
+ 2 + 1, у = – х + 6.
3. Если х > 3, то у = – (3 – х) – х
+ х + 2 + 1, у = х.
Функцию
записываем как кусочно-заданную:
у = 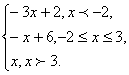
Подобно тому, как числовая прямая точками – 2 и 3
разбивается на промежутки, координатная
плоскость прямыми х = – 2 и х = 3
разбивается на части («полосы»), в каждой из
которых строим свой график. Заметим, что данная
функция непрерывна, поэтому на «границах» части
графика должны соединяться.
II. Этот
метод можно применять к функциям разных видов.
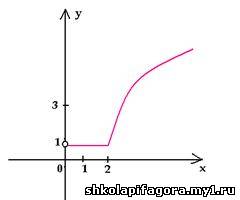
Например, построим график функции у = | log2
x – 1 | – log0,5 x.
Заметим, что х > 0.
1. Пусть log2x – 1 > 0, log2x >
1, x > 2, тогда у = log2 x – 1 +
log2 x; y = 2 log2 x – 1.
2. Пусть log2 x – 1 < 0, 0 < x < 2,
тогда у = – log2 x + 1 + log2 x; y
= 1.
Запишем функцию как кусочно-заданную:
у = 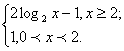
III. Рассмотрим некоторые частные случаи
функций, содержащих модуль.
1) у = | f(x) |.
По определению модуля имеем: | f(x) | = 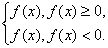
Таким образом , для того, чтобы построить график
такой функции, необходимо взять часть графика,
лежащую не ниже оси абсцисс, а часть графика,
лежащую ниже этой оси отобразить относительно
нее в верхнюю полуплоскость. (Заметим, что «–»,
стоящий перед функцией означает симметричное
отображение графика относительно оси абсцисс).
Например, построим график функции у = | x2
– 2х – 3 |.
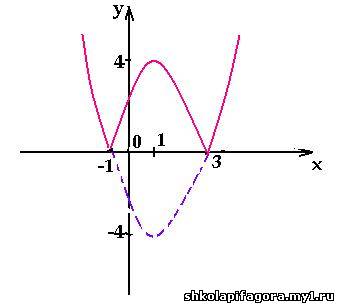
Построим сначала график функции у = х2
– 2х – 3. Графиком этой функции является
парабола, ветви которой направлены вверх.
Координаты ее вершины: х = 1, у = – 4. Точки
пересечения параболы с осями координат: (0; – 3); (–
1; 0); (3; 0). Далее выполняем отображение части
графика, лежащей в нижней полуплоскости,
относительно оси абсцисс.
2) у = f(| x |). Используем определение модуля: f(|
x |) = 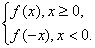
Чтобы построить график такой функции строим
график функции у = f(x) и берем ту его
часть, где х > 0 (в правой полуплоскости).
Затем эту часть симметрично отображаем в левую
полуплоскость, где х < 0. (Заметим, что
построение графика функции f(– x) и
состоит в отображении части графика, лежащей в
правой полуплоскости в левую относительно оси
ординат).
Например, построим график функции у = х2
– 2| х | – 3. Сначала строим график функции у
= х2 – 2х – 3, далее выполняем
указанные преобразования.
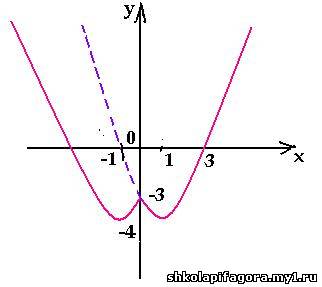
3) Построим график функции y = | f(| x
|)|, например, y = | x2 – 2| х | – 3 |,
выполним последовательно преобразования,
рассмотренные в пунктах 2 и 1.
4. Рассмотрим зависимость | y | = f(x).
Ее нельзя назвать функцией, так как не
выполняется условие: каждому значению х должно
соответствовать единственное значение у.
Рассмотрим построение графика такой
зависимости (можно говорить "графика
уравнения"). Используем определение модуля: у
= f(x), если у > 0, – у = f(x),
y = – f(x), если у < 0
Получаем, чтобы построить такой график, сначала
строим график функции у = f(x) и
берем ту его часть, которая лежит в верхней
полуплоскости, где у > 0; чтобы
построить график в нижней полуплоскости (где у
< 0), нужно построенную часть отобразить
симметрично относительно оси абсцисс (знак «–»
перед функцией и означает такое отображение)
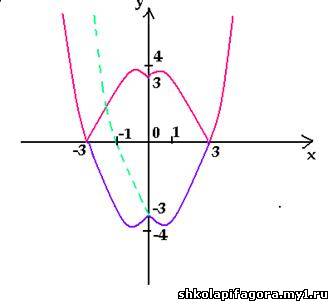
Например, построим график уравнения | y | = x2
– 2х – 3
Заметим, что графики, не относящиеся к
рассмотренным частным случаям, следует строить «
раскрывая модули на промежутках».
| x |
1 |
0 |
– 1 |
y |
0 |
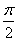
|
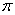
|
IV. Приведем некоторые примеры
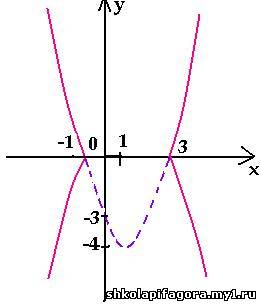
1. Построим график уравнения | y | = arccos| x
|.
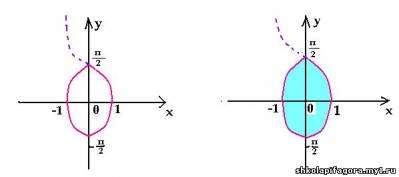
2. Графическим способом можно решать и
неравенства с двумя переменными. Например,
решением неравенства | y | < arccos| x |
являются координаты точек закрашенной части
плоскости, включая границы.
Решим еще одно задание, предлагавшееся на ЕГЭ:
найти все целочисленные решения неравенства | y
| < | | x – 2 | – 3 | (х0; у0),
для которых х0 = у0. Построим
сначала график уравнения | y | = | | x – 2 | –
3 |. Решением данного неравенства будут являться
координаты точек закрашенной части плоскости,
включая границы.
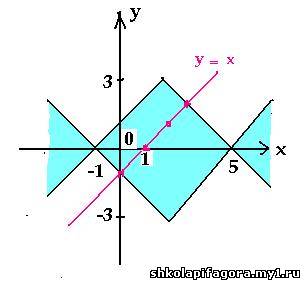
Пары чисел (х0; у0),
являющиеся решениями неравенства, для которых y0
= x0, являются координатами точек,
лежащих на прямой у = х. Выберем точки с
целыми координатами: (0; – 1); (1; 0); (2; 1); (3; 2), они и
будут являться решениями данной задачи.
3. Определить, сколько корней имеет уравнение | 3
– x | + log3| x | = 2 – x.
Запишем уравнение в виде | 3 – x | + x = log3|
x | + 2. В одной системе координат построим
графики функций y = | 3 – x | = x (1) и y
= log3| x | = 2 (2). Функцию (1) запишем как
кусочно-заданную, раскрывая модуль на
промежутках:
y = 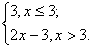
График функции (2) построим, выполняя
отображение графика y = log3x + 2
относительно оси ординат ( один из рассмотренных
частных случаев ).
Графики имеют две общие точки, следовательно,
данное уравнение имеет два корня.
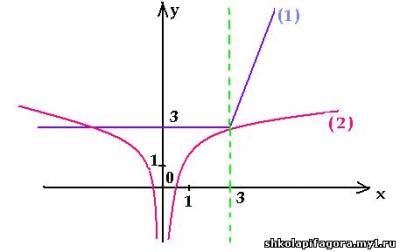
V. Для повторения материала, его закрепления
предлагаем выполнить следующие задания.
1. Постройте графики функций и уравнений: y = 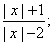 | y | = ; y | y | = ; y 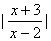 = | | 2 – x
| – 4 |; y = | x2 – 4 | x | + 3 |; y = = | | 2 – x
| – 4 |; y = | x2 – 4 | x | + 3 |; y = 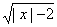 + 1. + 1.
2. Решите графически уравнения c одной и двумя
переменными: | 3 – x | – 3 = 2| x | – x2;
| y | = 2| x | – x2; 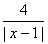 = | x – 2,5 | –1,5. = | x – 2,5 | –1,5.
3. Решите графически неравенства с двумя
переменными: | y | > x24x + 3;
| x | + | y | < 3.
4. Решите графически систему уравнений: 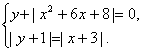
5. Найдите все значения а, при каждом из которых
уравнение | x + a | + | | x – 3 | – 4 | = 1
имеет ровно два корня.
| 
