Цели урока:
- развитие умений обобщать, абстрагировать и
конкретизировать свойства изучаемых объектов и
отношений, и применять их при решении
практических задач;
- выработка умений оценивать свой уровень
познания темы;
- развитие культуры устной речи, познавательного
интереса;
- развитие умений преодолевать трудности при
решении математических задач.
Оборудование: мультимедиа, таблицы
самооценки.
Структура урока:
- Ознакомление с темой урока, постановка его
целей.
- Оценка учащимся уровня познания темы.
- Повторение теоретического материала.
- Умение решать геометрические задачи.
- Умение решать задачи прикладного характера.
ХОД УРОКА
1. Организационный момент.
Ознакомление с темой и целями урока.
2. Проверка знаний теоретического материала
по теме "Подобные треугольники”.
Проверка осуществляется с помощью слайдов,
выполненных с помощью программы Power Point
Какие треугольники
называются подобными? |
Признаки подобия треугольников.
Найдите подобные треугольники и докажите их
подобие: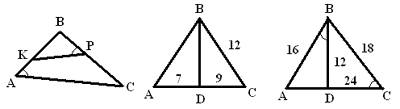
|
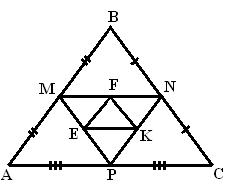
Отношение периметров подобных треугольников:
M, N, P, E, F, K – середины сторон
PEFK = 4 cм
PABC – ? |
Отношение линейных элементов подобных
треугольников.
Продолжить: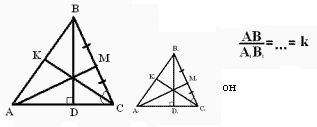
|
Отношение площадей подобных
треугольников.
Сформулировать теорему. |
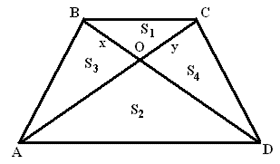
Основания трапеции относятся как m : n.
Найдите в каком отношении делится площадь
трапеции ее диагоналями. - Пусть OB = x, OC = y,
Треугольники BOC и AOD подобны с k = …
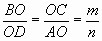
Тогда OD =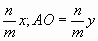 
2. S2 = _________ S1(по теореме ________________).
S3 = _________ S1(по теореме ________________).
S4 = _________S1 (по теореме ________________).
3. S1 : S2 : S3 : S4 = ______ : ______ :
______ : ______. |
Свойство биссектрисы
треугольника выражается отношением …
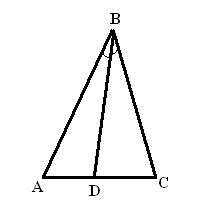
|
Теоремы о среднем. 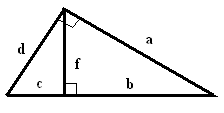
Для данного треугольника справедливы
равенства
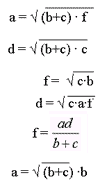
|
Вопросы на
"засыпку”.
- В повседневной жизни нам часто приходится
сталкиваться с различными проявлениями подобия,
однако подобие в обыденном смысле и с
математической точки зрения – не одно и то же.
Поэтому ответьте на вопрос: будут ли подобными
две банки емкостью 3 л и 1 л?
- Будут ли подобны два четырехугольника, у
которых соответственно равны все углы?
- Из отрезков длиной 4, 6, 8, 9, 12 и 18 составили два
подобных между собой треугольника. Найти
коэффициент подобия этих треугольников.
|
3. Проверка домашней работы.
В равнобедренном
треугольнике AB = BC = 5. На стороне BC взята точка D
так, чтобы BD = 1. Отрезок AD пересекает высоту BE в
точке K. Найдите: 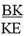 |
Первый способ решения:
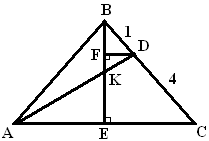

|
Второй способ решения:
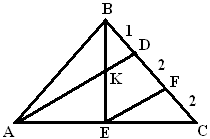
Проведем среднюю линию 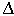 ADC. По теореме Фалеса: ADC. По теореме Фалеса:
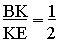
|
4. Решение задач прикладного характера.
Так как при решении текстовых задач по алгебре
будем использовать графики равномерного
движения, целесообразно повторить теоретический
материал известный учащимся из курса физики. На
левой части доски заранее выполнены записи,
правая часть доски заполняется непосредственно
на уроке учащимися.
- Уравнение прямой.
y = kx + b
|
Равномерное прямолинейное движение Координата
тела в любой момент времени
x = xo + Vt |
k = tg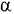 угловой коэффициент прямой
угловой коэффициент прямой |
tg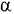 = Vтела = Vтела |
S = V · t
если V1 = V2,
если S1 = S2,
если t1 = t2, |
то 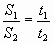 то 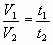 
то 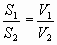 |
|
5. Заключительный этап урока состоит в
подведении итогов оценивания.
| 
