Результаты:
- Владеть основными теоретическими понятиями
темы.
- Уметь вычислять площади криволинейных фигур
при помощи интеграла.
ХОД ЗАНЯТИЯ
I. Организационный момент
1) Предварительное определение уровня знаний –
6 мин.
2) Мотивация – 2 мин.
(Задание 8)
Организация самостоятельной работы
студентов по основным вопросам занятия – 23
мин.
- Деятельность преподавателя: Организует
работу студентов по основным вопросам темы
занятия.
- Деятельность студентов: Самостоятельно
работают по основным вопросам темы занятия:
- определение криволинейной трапеции;
- формула Ньютона-Лейбница;
- примеры вычисления площадей криволинейной
трапеции при помощи интеграла.
II. Подведение итогов занятия.
1) Проверка степени усвоения материала – 12 мин.
(Задание 8.2)
2) Заполнение дневников – 2 мин.
Задание 8
III. Предварительное определение уровня
знаний
Ф.И. (выполняющего)______________________________
Ф.И. (проверяющего) ______________________________
Задание 1. Вспомните формулы
первообразных и правила вычисления
первообразных, составив таблицу:
| Функция f (x) |
Общий вид первообразных для f (x) |
| f (x) = k (постоянная) |
F (X) = |
| f (x) = xn, n =/= –1 |
F (X) = |
| f (x) = cosx |
F (X) = |
| f (x) = sinx |
F (X) = |
f (x) = 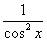 |
F (X) = |
f (x) = 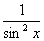 |
F (X) = |
f (x) = 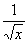 |
F (X) = |
| f (x) + g(x) |
|
| k * f (x) |
|
| f (kx + b) |
|
Задание 2. Найдите общий вид
первообразной для функции f (x) = sin x – 10х4
+ 3, график которой проходит через точку М (0; 5).
Задание 8.1
IV. Закрепляющий материал
Задание 1. Ответьте устно на вопросы:
а) Какая фигура называется криволинейной
трапеции?
б) Какими свойствами она обладает?
в) По какой формуле вычисляется площадь
криволинейной трапеции?
г) Как вычислить площадь фигуры, ограниченной
линиями:
- у = х2 + 1 и y = 2х + 4 (слайд 9);
- у = х2 и y = х2 – 9х + 18,25
(слайд 10)?
д) Как найти площадь изображенной на рис. 10
фигуры?
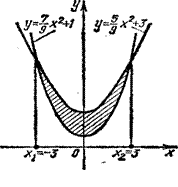
Рис.10
Задания 2-3. Найти площадь
фигуры, ограниченной указанными линиями:
1) у = 3x2 – 1, x = 1, x = 2 и осью ОХ;
2) у = cos х, у = 1/2, х = 0 и х =  /3. /3.
(продемонстрировать на интерактивной доске).
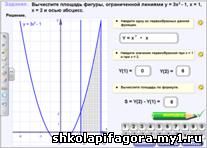
Задания 4-6. Попытайтесь, используя
таблицу первообразных и формулу вычисления
площади криволинейной трапеций, найти площадь
фигуры, ограниченной указанными линиями:
1) у = 12х – 3x2 и y = 0;
2) у = sin х, у = 2, х = 0 и х = п;
3) у = x2, y = 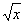 . .
(по одному примеру студенты решают у
интерактивной доски).

Задание 8.2
| 
