Цель урока: вывести формулы
сокращенного умножения 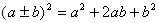 и показать их применение к решению
задач. и показать их применение к решению
задач.
Задачи урока:
- Образовательные: вывести формулы квадрата
суммы и квадрата разности двух выражений;
научить применять их в преобразованиях
выражений; рассмотреть тождества:
 - Развивающие: развитие алгоритмического
мышления, памяти, внимательности; развитие
познавательного интереса учащихся; развитие
культуры устной речи.
- Воспитательные: усиление познавательной
мотивации учащихся осознанием своей
значимости в образовательном процессе; развитие
взаимовыручки и взаимопомощи,
самостоятельности.
ХОД УРОКА
I Организационный момент
Учитель: Здравствуйте, ребята! Тему
нашего урока мы сформулируем немного позже. А
сейчас, опираясь на знания ранее
пройденного материала, постараемся вплотную
подойти к теме нашего урока.
II Актуализация знаний
(на доске заранее записаны задания, задания 1-3
выполняются устно; задание 4 – ученик выполняет у
доски)
- Найти квадраты выражений:
 - Прочитайте выражения, записанные на
доске:
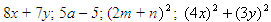 ; ;  - Выполните действия:
 - Выполните умножение многочленов

III Изложение нового материала
(исследовательская работа)
Учитель: Обратите внимание на
последнее задание, как иначе можно записать
произведение двух многочленов?
Учитель записывает на доске: 
Получили, что = 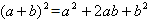 .
Это одна из формул сокращенного умножения,
которые нам предстоит с вами изучить на
сегодняшнем и последующих уроках. Эта формула
называется формулой квадрата суммы и
позволяет проще выполнять возведение в квадрат
суммы любых двух выражений. .
Это одна из формул сокращенного умножения,
которые нам предстоит с вами изучить на
сегодняшнем и последующих уроках. Эта формула
называется формулой квадрата суммы и
позволяет проще выполнять возведение в квадрат
суммы любых двух выражений.
Давайте проверим это на примере возведем в
квадрат число 101 без формулы и с применением ее.
(Первым способом вычисляет ученик у доски,
вторым – предлагается выполнить устно сильному
ученику)
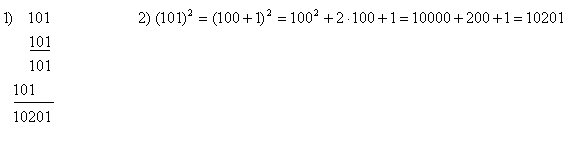
Вычисляя двумя разными способами, мы
получили один и тот же результат. Какой
прием вычислений более рациональный?
Откройте тетради и запишите тему сегодняшнего
урока «Возведение в квадрат суммы и
разности двух выражений».
– Запишите формулу  в тетрадь и послушайте, как она
читается: квадрат суммы двух выражений
равен квадрату первого выражения, плюс
удвоенное произведение первого и второго
выражений, плюс квадрат второго выражения. в тетрадь и послушайте, как она
читается: квадрат суммы двух выражений
равен квадрату первого выражения, плюс
удвоенное произведение первого и второго
выражений, плюс квадрат второго выражения.
(Повторить всем классом хором)
– Давайте посмотрим, что изменится, если вместо
суммы двух выражений взять их разность?
Выполним умножение двумя способами:
1) как умножение многочлена на многочлен;
2) рассматривая разность как сумму первого
слагаемого и слагаемого, противоположного
второму.
(Первым способом решает ученик: 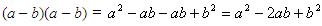 ; вторым –
учитель: ; вторым –
учитель:  . .
Получили, что  .
Эта формула называется формулой квадрата
разности. Она позволяет возводить в квадрат
разность любых двух выражений. Запишите эту
формулу в тетрадь и давайте вместе прочитаем ее :
квадрат разности двух выражений равен
квадрату первого выражения, минус удвоенное
произведение первого и второго выражений, плюс
квадрат второго выражения. .
Эта формула называется формулой квадрата
разности. Она позволяет возводить в квадрат
разность любых двух выражений. Запишите эту
формулу в тетрадь и давайте вместе прочитаем ее :
квадрат разности двух выражений равен
квадрату первого выражения, минус удвоенное
произведение первого и второго выражений, плюс
квадрат второго выражения.
IV. Закрепление изученного
Преобразуйте многочлен ( учащиеся по одному
выходят к доске, остальные – в тетради):
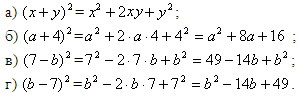
Сравнивая результаты двух
последних примеров, мы видим, что получили
один и тот же результат:  . .
Докажем тождество  . .
Для этого мы должны вспомнить:
1) Что такое тождество? (Это равенство, верное
при любых значениях переменных);
2) Способы доказательства тождеств
1)
преобразовать левую часть в правую или правую
часть в левую;
2) показать, что левая и правая
части исходного равенства тождественно равны
одному и тому же выражению; 3) рассмотреть
разность между левой и правой частями равенства
и доказать, что разность равна нулю).
Запишем доказательство в тетрадь, показав, что
левая и правая части равенства тождественно
равны одному и тому же выражению:
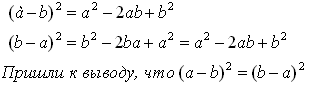
Рассмотрим еще два примера
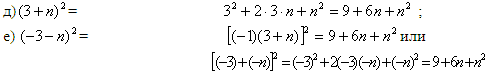
и докажем еще одно тождество:  (доказательство проводит
учитель, учащиеся записывают его в тетрадь). (доказательство проводит
учитель, учащиеся записывают его в тетрадь).
Доказательство: Игра «Смотри не ошибись» (учащиеся
по одному выходят к доске и вместо многоточия
вписывают букву или число) 2. У вас на столах лежат карточки с заданием,
выполнив которое, вы узнаете зашифрованное
в ней слово.(задания выполняются в
тетрадях, ответы даны на доске, учащиеся
рядом с получившимся ответом ставят букву)
Представьте в виде многочлена: Ответы:

(Получившееся слово: МОЛОДЕЦ)
V. Домашнее задание
1. п. 31 ( уч. Алгебра 7 класс, авторы: Ю.Н.Макарычев,
Н.Г.Миндюк и др.), № 860, № 863
2. (опережающее) Вывести формулу куба суммы и
куба разности двух выражений ;
3. Каждому составить карточку с 8-10
формулами, в которых недописаны правые
части;
VI. Подведение итогов
На уроке мы познакомились с новыми
формулами – одними из формул сокращенного
умножения: (a + b)2 = a2
+ 2ab + b2. Эти формулы позволяют
сократить время на вычисление квадрата суммы и
разности двух выражений. Давайте еще раз
повторим, как возвести в квадрат сумму (разность)
двух выражений. (Учащиеся проговаривают
правила)
| 
