Цели:

Тип занятия: дидактическая игра.

Оборудование: компьютер (если использовать презентацию) или  таблицы c готовыми рисунками.

ХОД ЗАНЯТИЯ

I. Вступительное слово учителя

II. Устные задачи шутки

а)  Шесть рыбаков съели за шесть дней шесть судаков. За сколько дней десять рыбаков съедят десять судаков? (Аппетит одинаковый)
б) Яйцо всмятку варится три минуты. Сколько времени потребуется, чтобы сварить всмятку пять яиц?
в) Два отца и три сына купили два апельсина. Каждому досталось по апельсину. Как это могло случиться?
г) Двое подошли к реке. У берега стояла лодка, которая может вместить лишь одного. Но оба переправились. Как это могло случиться?
д) Летели утки: одна впереди и две позади, одна позади и две впереди, одна между двумя и три в ряд. Посчитай, сколько всего летело уток?
е) Сколько получится десятков, если три десятка умножить на три десятка?
ж) В семье у семи братьев по одной сестре. Сколько всего детей?
з) У одного человека спросили, сколько у него детей. Ответ его был таков: «У меня столько сыновей, сколько и дочерей, а у каждого сына по три сестры». Сколько детей в этой семье?
и) Птицелов поймал пять синиц, на дороге встретил пять учениц. Каждой подарил по птицы и в клетке осталась одна. Как это могло случиться?
к) Число 666 увеличили в полтора раза, не производя над ним никаких арифметических действий. Как это сделали?
л) Раздели 188 пополам так, чтобы получилась единица. Как это сделали?
м) на сковороде помещается 2 кусочка хлеба. На поджаривание с одной стороны уходит 1 минута. Как  поджарить за 3 минуты три кусочка хлеба с  обеих сторон?

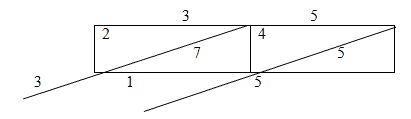
III. Умножение «Решеткой»

Старинный способ умножения решеткой заключается в следующем: по сторонам  заранее вычерченной решетки записываются сомножители. Произведения каждой пары цифр записываются в соответствующий квадрат решетки, причем десятки отделяются диагональной чертой от единиц. Результат – произведение получается, если сложим цифры, расположенные между диагональными линиями.

35*9

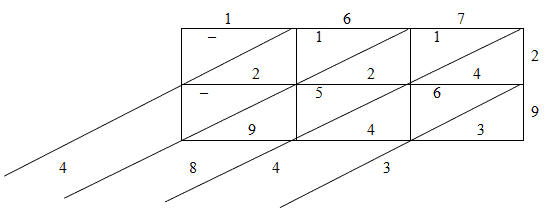
Умножим 167 на 29

IV. Старинные задачи

2500 лет назад в Греции уже умели довольно хорошо решать уравнения с одним неизвестным и системы уравнений. Независимо от греков этими приемами овладели и китайцы, а позднее и индийцы.
Вот несколько старинных задач.

1) Задача в стихах из так называемой «Греческой Антологии»:

– Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы?
– вот, сколько, – ответил философ,– половина изучает математику, четверть – музыку, седьмая часть пребывает в молчании и, кроме того, есть еще три женщины.
Сколько учеников у Пифагора?

Решение: Х – число всех учеников,
1/2х + 1/4х + 1/7х + 3 = х, откуда х = 28

2) Древняя китайская задача.

В клетке находиться неизвестное число фазанов и кроликов. Известно только, что вся клетка содержит 35 голов и 94 ноги. Требуется узнать число фазанов и число кроликов.

3) Задача Древней Греции.

– Хроноса (бога времени) вестник, скажи, какая часть дня миновала?
– Дважды две трети того, что прошло, остается. (У древних греков день делился на 12 часов)

4) Старинная русская задача.

В 336-ведерное водохранилище всякие два часа одной трубой втекает воды 70 ведер, другою трубою вытекает 42 ведра. Спрашивается, в какое время то водохранилище наполниться.

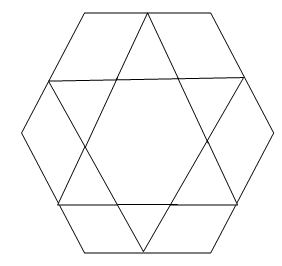
V. Геометрические задачи

Сосчитайте сколько треугольников в фигуре?

VI. Итог урока

– Понравилась вам сегодня математика?
– Что запомнилось особенно?