Цели.

1. Придать предмету привлекательность и поднять к нему интерес, возбудить охоту самостоятельно восполнять пробелы своей подготовки по учебным книгам. Заразить любовью к миру чисел, к бесконечному ряду цифр.

2. Убедить, что овладеть приемами и методами быстрого счета может каждый, что приемы устного счета способствуют развитию памяти и мышления.

1. Иллюстрация картины Богданова-Бельского "Устный счет”.

2. Формирование 6 групп по 2–3 ученика, готовящих материал по предложенным вопросам

1. Вступительное слово.
2. Картина "Устный счет”.
3. История числа 365.
4. С. А.Рачинский.
5. Народная школа.
6. "Арифметические забавы”.
7. Упражнения в устном счете.
8. Дружеский шарж.

1. Устные вычисления дают возможность не только быстро производить простые расчеты в уме, они развивают память и помогают полноценно усваивать предметы физико-математического цикла. Свободное устное выполнение счетных операций в значительной степени может свидетельствовать о незаурядности вашего интеллекта, что может вызвать немалое удивление и даже восхищение товарищей и знакомых. Устный счет вырабатывает навык запоминания чисел, выявления особенностей отдельных чисел.

2. Картина "Устный счет" Н. П. Богданова-Бельского была написана в 1895 году, находится в Третьяковской галерее. Написана картина в 1896 г. в селе Татево, расположенном в живописном месте Калининской области (бывший Бельский уезд Смоленской губернии). Художник изобразил на своей картине невыдуманных учеников и учителя. Учитель – это Сергей Александрович Рачинский, известный русский педагог, замечательный представитель русских образованных людей позапрошлого века. Он был доктором естественных наук и профессором ботаники Московского университета. В 1868 г. С.А. Рачинский решает "уйти в народ". Он держит экзамен на звание учителя начальных классов. На свои средства открывает школу для крестьянских детей в селе Татево Смоленской губернии и становится в ней учителем. Его ученики так хорошо считали устно, что этому удивлялись все посетители школы. Неслучайно, художник изобразил С.А. Радчинского вместе с его учениками именно на уроке устного решения задач. Эта картина – гимн учителю и ученику. Учитель слушает ученика внимательно. А какую же задачу дал им учитель? Вот она: (10² + 11² + 12² + 13² + 14²):365.

3. История числа 365.

1) Оно замечательно, прежде всего, тем, что определяет число дней в году.

2) Далее, при делении на 7 оно дает в остатке 1, эта несущественная, казалось бы, особенность числа 365 имела большое значение для старого семидневного календаря.

3) Другая особенность числа 365 не связана с календарем:

365 = 10² + 11² + 12², т.е. 365 равно сумме квадратов трех последовательных чисел, начиная с 10: 100 + 121 + 144 = 365.

4) Но и это еще не все, – сумма квадратов двух следующих чисел 13 и 14: 13² + 14² = 169 + 196 = 365.

5) На указанном свойстве числа 365 основана задача С.А.Рачинского, изображенная на известной картине Богданова – Бельского:

(10² + 11² + 12² + 13² + 14²):365 = (365 + 365):365 = 2

4. С. А.Рачинский. Во второй половине XVIII в. Екатерина II подарила Бельский уезд с 40 тыс. крестьян графу Потемкину, который выдал свою дочь Ольгу замуж за Антона Рачинского. В этих владениях Рачинский и избрал место для закладки барской усадьбы. (Дворянский дом, напоминающий греческую виллу, был разрушен в годы Великой Отечественной Войны.) После смерти Антона Рачинского наследником остался его сын Александр. Александр Антонович Рачинский вырастил 6 детей: 4 сына и 2 дочери. Все они получили высшее образование. Сыновья работали на государственных должностях. Все Рачинские похоронены в этом селе. До наших дней сохранились памятники Сергею Александровичу и Марии Толстой, урожденной Рачинской, которая была замужем за сыном Л. Н. Толстого Сергеем Львовичем. Из всех Рачинских особого внимания заслуживает Сергей Александрович – крупный ученый, профессор Московского университета. Он был знаком и переписывался с П. И.Чайковским и Ф. Листом, с В. А. Серовым и Л. Н. Толстым.

5. Народная школа. В 1872 г. С. А. Рачинский уехал из Москвы в Татево и вскоре стал преподавать в народной школе, открытой его сестрой Марией. Он жил при школе, полностью посвятил себя обучению крестьянских детей. Во время преподавания в начальной школе С.А. Рачинский написал книги: "1001 задача для умственного счета", " Арифметические забавы", "Геометрические забавы" и др. В последние годы жизни С.А. Рачинский начал закладку кирпичного здания (ныне в этом здании находится Татевская средняя школа). Школа была достроена уже после его кончины. Она была открыта в 1907 г. Сергей Александрович заботился о продолжении образования своих одаренных учеников. Так, при его содействии получил художественное образование Н.П. Богданов-Бельский. Профессор определил его в иконописное училище при Троице-Сергиевой лавре, а затем в Московскую школу живописи и ваяния. По ее окончании художник поселяется в Татеве, в доме Рачинского. Здесь рождаются картины "У дверей школы", "У больного учителя", "Дети на уроке", "Устный счет", на которых изображены деды и прадеды тех, кто живет и сейчас в Татеве. В Татеве помнят С.А. Рачинского и бережно относятся ко всему, что связано с ним. В школе создан музей, посвященный истории села, деятельности С.А. Рачинского и Н.П. Богданова-Бельского. В музее собраны уникальные экспонаты.

6. "Арифметические забавы”. Будучи незаурядным человеком, он сначала сам прекрасно изучил свойства чисел, делимость их, свойства простых чисел. Его стала интересовать арифметика как наука, и он понял, что если применить важнейшие теоремы теории чисел к простейшим арифметическим расчетам, то можно добиться больших успехов. Главным в преподавании он считал знакомство с числами, т.е. ясное сознание их состава из первичных множителей. В своей статье "Арифметические забавы" С.А.Рачинский указывает довольно оригинальный способ устного умножения на число, записанное только одними девятками.

1. Этот способ заключается в следующем. Для того чтобы найти произведение числа, написанного одними девятками, на число, имеющее с ним одинаковое количество цифр, надо от множителя отнять единицу и к получившемуся числу приписать другое число, все цифры которого дополняют цифры числа до 9.

Примеры:

2. Способ возведения в квадрат любого двузначного числа. Если запомнить квадраты всех чисел от 1 до 25, то легко найти и квадрат любого двузначного числа, превышающего 25. Рачинский указывает для этого следующий способ. Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю.

Примеры.

37² = 12х100 + 13² = 1200 + 169 = 1369

58² = 33х100 + 8² = 3364

93² = 68х100 + 43² = 6800 + 18х100 + 7² = 8649

Докажем это предложение в общем виде. Пусть данное двузначное число М = 10m + n. Для того чтобы найти квадрат этого числа, С.А.Рачинский предлагает произвести следующие действия:

(10m + n – 25)100 + (50 – 10m – n )² =

=1000m + 100n – 2500 + 2500 + 100m² + n² – 1000m – 100n + 20mn =

=100m² + 20mn + n² = (10m + n)².

3. Еще один способ умножения двузначных чисел. В своей статье С.А. Рачинский приводит еще один довольно любопытный способ умножения двузначных чисел. Хотя при помощи этого способа можно найти произведение только таких двузначных чисел, у которых сумма единиц равна 10, но при устном счете он может быть полезен. Пусть даны да двузначных числа, у которых сумма единиц равна 10.

Составим их произведение.

MxK = (10m + n)(10a + 10 – n ) = 100am + 100m – 10mn + 10an + 10n – n² =

= m(a +1)100 + n(10a + 10 – n ) – 10mn = m(a + 1)100 + n(K – 10m).

Присмотревшись к результату, нетрудно указать правило умножения таких двузначных чисел.

А придумал этот прием совершенно самостоятельно один из учеников Сергея Александровича. Вот что ученый писал по этому поводу: "Этот прием – измышление 12-летнего мальчугана, усердствовавшего в моей школе по части умственного счета, удивившего меня мгновенным умножением 43 на 87.

Итог урока. Диптих: "История и современность”.

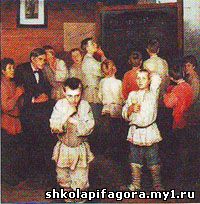Рисунок 1. Картина Богданова-Бельского "Устный счет”.	Рисунок 2. Дружеский шарж.