1. Введение
Если ставится задача для каждого значения a из некоторого множества A решить уравнение F(x,a) = 0 относительно x, то уравнение F(x,a) = 0 называется уравнением с параметром a, а множество A - областью изменения параметра.
Решить уравнение F(x,a) = 0 с переменной xи параметром a - это значит на подмножестве A множества действительных чисел решить семейство уравнений, получающихся из уравнения F(x,a) = 0 при всех значениях параметра a.
Ясно, что написать каждое уравнение из бесконечного семейства уравнений
невозможно. Тем не менее, каждое уравнение семейства должно быть
решено. Сделать это можно, если, например, по некоторому целесообразному
признаку разбить множество всех значений параметра на подмножества и
решить затем заданное уравнение на каждом из этих подмножеств.
Для разбиения множества значений параметра на подмножества удобно
воспользоваться теми значениями параметра, при которых, или при переходе
через которые, происходят качественные изменения уравнения. Такие
значения параметра будем называть контрольными.
Покажем на примерах, как эти значения параметра обнаруживаются, как с
их помощью множество значений параметра разбивается на подмножества и
как затем на каждом подмножестве решается заданное уравнение (система
уравнений, неравенство).
2. Показательные и логарифмические уравнения
Рассмотрим решение показательных и логарифмических уравнений с параметром на конкретных примерах.
Пример 1
Найти все значения параметра a, при которых уравнение 21g(x + 3) = lg ax имеет единственный корень.
Решение:
Данное уравнение эквивалентно системе:
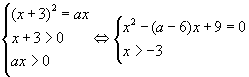
Квадратное уравнение имеет единственное решение, если D = 0, то D = (a - 6)2 – 4 • 9 = a2 – 12a. D = 0 при a = 12. Если a = 0, то x = -3 ∉ (-3; +∞). Если a = 12, то 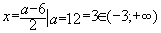 . .
При D > 0 квадратное уравнение может иметь два решения, а
исходное уравнение – только одно из двух, если другое решение
квадратного уравнения не удовлетворяет условию x > -3. Это возможно, если корни квадратного уравнения расположены по разные стороны от точки x = -3. Поэтому, если значение квадратного трехчлена в точке x > -3 отрицательно, т.е. (-3)2 + 2(a - 6) + 9 < 0, то больший корень квадратного уравнения будет справа от точки x = -3, а меньший – слева. Таким образом, при a < 0 данное уравнение будет иметь одно решение.
Ответ: уравнение имеет одно решение при a = 12, a < 0.
Пример 2
При каких значениях параметра уравнение a ∙ 2x + 2x - 1 - 5 = 0 имеет единственное решение?
Решение:
Введем обозначение 2x = t. Уравнение принимает вид: a ∙ t + 1 / t - 5 = 0, или a ∙ t2 - 5t + 1 = 0. Если a = 0, то t = 1 / 5, 2x = 1 / 5, x = -log2 5. Если a > 0, D = 0, т.е. 25 - 4a = 0, a = 25 / 4, то t = 2 / 5, 2x = 2 / 5, x = log2 2 / 5 - единственное решение. Если a > 0, D < 0, то исходное уравнение не имеет решения, т.к. не имеет решения квадратное уравнение. Если a < 0, то D = 25 - 4a
всегда положительный, следовательно квадратное уравнение всегда имеет
два корня, причем один из корней положительный, а другой –
отрицательный, т.к. t1 ∙ t2 = 1 / a < 0 при a < 0, поэтому исходное показательное уравнение имеет единственное решение.
Ответ: уравнение имеет единственное решение при a ≤ 0, a = 25 / 4.
Пример 3
Найти все значения параметра, при которых уравнение x + log1 / 3(9x - 2a) = 0 имеет два различных решения.
Решение:
Используя определение логарифма и свойства степеней, запишем уравнение в виде: 32x - 2a = 3x. Введем новое переменное t = 3x, тогда уравнение имеет вид t2 - t - 2a = 0. Его дискриминант D = 1 + 8a. Квадратное уравнение имеет два решения, если оба корня квадратного уравнения положительные и удовлетворяют условию 9x - 2a > 0, т.е. t2 - 2a > 0. Из квадратного уравнения t2 - 2a = t, поэтому условие выполняется при всех положительных t.
| По теореме Виета для квадратного уравнения | 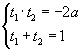 | откуда оба корня положительные при a < 0. |
Объединяя условия существования двух различных корней квадратного уравнения и их положительности, получаем: a ∈ (-1 / 8; 0).
Ответ: Уравнение имеет два различных решения при a ∈ (-1 / 8; 0).
Пример 3
| Решить уравнение | 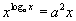 . . |
Решение:
Логарифмическая функция определена только при a > 0, a ≠ 1, поэтому при a ≤ 0, a = 1 уравнение не определено и, следовательно, не имеет решения. Решим уравнение при a > 0, a ≠ 1. О.Д.З. x > 0, x ≠ 1. Прологарифмируем обе части уравнения по основанию a. 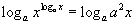 . На основании свойств логарифмов получаем уравнение loga2 x = 2 + loga x. Введем вспомогательную переменную t = loga x. Квадратное уравнение t2 - t - 2 = 0 имеет корни t1 = 2, t2 = -1. Поэтому loga x = 2, loga x = -1, откуда x1 = a2, x2 = 1 / a. Оба корня принадлежат области допустимых значений при a > 0, a ≠ 1. . На основании свойств логарифмов получаем уравнение loga2 x = 2 + loga x. Введем вспомогательную переменную t = loga x. Квадратное уравнение t2 - t - 2 = 0 имеет корни t1 = 2, t2 = -1. Поэтому loga x = 2, loga x = -1, откуда x1 = a2, x2 = 1 / a. Оба корня принадлежат области допустимых значений при a > 0, a ≠ 1.
Ответ: при a ≤ 0, a = 1 x ∈ ∅, при a > 0, a ≠ 1 x1 = a2, x2 = 1 / a.
Решите следующие примеры самостоятельно.
1. Найти все значения параметра, при каждом из которых уравнение log2(4x - a) = x имеет два различных решения.
2. Найти все значения параметра, при каждом из которых уравнение log3(9x + 9a3) = x имеет два различных решения.
| 3. Решите уравнение | 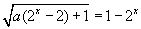 | . |
| 4. Решите уравнение | 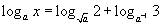 | . |
5. Решите уравнение 4x - 4m∙n∙2x + 2m + 2 = 0.
6. Решите уравнение 4x - 2a(a + 1)2x - 1 + a3 = 0.
7. Решите уравнение lg2 x - lg x + a = 0.
8. При каких значениях параметра уравнение 144-∣2x - 1∣ - 2∙12-∣2x - 1∣ + a = 0 имеет хотя ьы одно решение?
| 9. Решите уравнение |
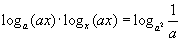 |
. |
| 10. Решите уравнение | 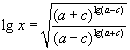 | . |
Ответы:
1. a ∈ (-1 / 4; 0).
| 2. |
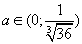 |
. |
3. При a ∈ (0; 1] x = log2 a.
4. При a ∈ (0; 1) ∪ (1; +∞) x = 3 / 4.
| 5. При | 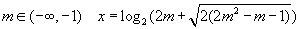 | , при m = 1 x = 1, при | 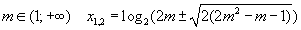 | , при m ∈ [-1; 1] x ∈ ∅. |
6. При a ∈ (0; +∞) x1 = 2log2 a, x2 = log2 a, при a = 0 x ∈ ∅, при a ∈ (-∞; 0) x = log2 a2.
| 7. При a ∈ (-∞; 1 / 4] |
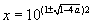 | . |
8. a ∈ (0; 1].
| 9. При | 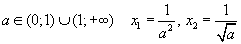 | . |
10. x = 10.
3. Показательные и логарифмические неравенства
Пример 1
| Решите неравенство | 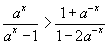 | . |
Решение:
При a ≤ 0 и a = 0 показательная функция не определена, следовательно, неравенство не имеет решения.
| Рассмотрим решение неравенства при a > 0, a ≠ 1 | 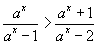 | . |
Введем вспомогательную переменную ax = z.
| Тогда неравенство принимает вид | 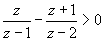 | или | 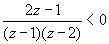 | . |
Решив алгебраическое неравенство методом интервалов, получим z ∈ (-∞; 1 / 2) ∪ (1; 2),
| или | 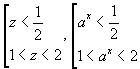 | . |
Монотонность показательной функции зависит от величины основания, следовательно,
| при a ∈ (0; 1) совокупность неравенств принимает вид | 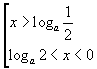 | , |
| а при a ∈ (1; +∞) | 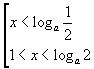 | . |
Неравенство решено.
Ответ: при a ∈ (-∞; 0], a = 1 x ∈ ∅, при a ∈ (0; 1) loga 2 < x < 0, x > -loga 2, при a ∈ (1; +∞) 0 < x < loga 2, x < -loga 2.
Пример 2
| При каких значениях параметра неравенство | 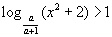 |
выполняется при всех значениях x? |
Решение:
| При | 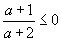 | и | 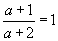 | логарифмическая функция не определена, |
и, следовательно, неравенство не имеет решения при a ∈ [-2; -1]. Рассмотрим решение неравенства при a ∈ (-∞; -2) ∪ (-1; +∞). Т.к. x2 + 3 > 0 при всех x,
| то | 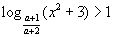 | может быть только при | 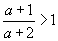 | . |
| Поэтому исходное неравенство эквивалентно системе: | 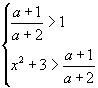 | или | 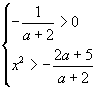 | . |
Чтобы последнее неравенство из системы выполнялось при всех значениях x, необходимо условие отрицательности его правой части,
| поэтому | 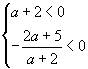 | или | 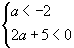 | , следовательно a < -2,5. |
Ответ: a ∈ (-∞; -2,5).
Решите следующие упражнения самостоятельно.
1. Решите неравенство loga x + 2 > 3logx a.
| 2. При каких значениях параметра неравенство | 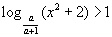 |
верно при любом действительном значении x? |
3. Решите неравенство a4∙4x - 33a∙2x + 8 > 0.
4. Решите неравенство a2∙42x + 1 - 65a∙4x - 1 + 1 > 0.
5. Найдите все действительные значения параметра, при которых неравенство a∙9x + 4(a - 1)∙3x + a > 1 выполняется при всех x.
6. Найдите все действительные значения параметра, при которых неравенство 1 + log2(2x2 + 2x + 7 / 2) ≥ log7(cx2 + c) имеет хотя бы одно решение.
7. Найдите все действительные значения параметра, при которых неравенство 1 - log1 / 7(x2 + 1) ≥ log7(ax2 + 4x + a) справедливо при всех x.
8. Решите неравенство a2 - 2∙4x + 1 - a∙2x + 1 > 0.
Ответы:
1. При a ∈ (-∞; 0], a = 1 x ∈ ∅, при a ∈ (0; 1) x ∈ (0; a) ∪ (1; 1 / a3), при a ∈ (1; +∞) x ∈ (1 / a3; +∞).
2. a ∈ (-∞; -2).
3. При a ∈ (-∞; 0] x ∈ R, при a ∈ (0; +∞) x < -2 - log2 a, x > 3 - log2 a.
4. При a ∈ (-∞; 0] x ∈ R, при a ∈ (0; +∞) x > log4 (4 / a), x < log4 (1 / 16a).
5. a ∈ (1; +∞).
6. c ∈ (0; 8].
7. a ∈ (2; 5].
8. При a ∈ (-∞; 0) x < 2 + log2(-a), при a = 0 x ∈ ∅, при a ∈ (0; +∞) x < log2 a + 1.
| 
