Цели урока:

1. Познакомить учащихся с практическими способами измерения длины окружности и площади круга.
2. Развитие математической речи учащихся, формирование умений анализа, синтеза.
3. Формирование навыков коллективной творческой деятельности.

Оборудование урока:

• Медиапроектор.
• Компьютер.
• Раздаточный материал:
• цилиндры,
• круги различных радиусов,
• палетка.
• Циркули,
• Транспортиры.
• Плакаты с формулами.
• Сигнальные карточки.

Ход урока:

I. Устная работа:

1. Решить пропорции: х:42=5:70 42:х=21:2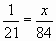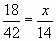 

С помощью сигнальных карточек показать правильный ответ:

1. х=6
2. х=4
3. х=3

2. Найти квадрат числа, используя плакат "Квадраты натуральных чисел от 10 до 99”: 42, 24, 56, 63, 91, 18.

3. Найти ошибку в рассуждениях и с помощью сигнальных карточек выразить свое мнение: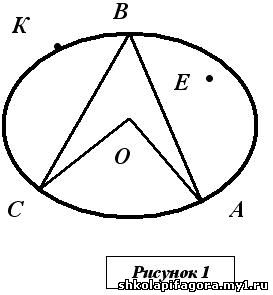

• если d = 15 см, то r = 30 см;
• центральный угол – это угол АВС;
• точка Е принадлежит только окружности;
• а точка К принадлежит только кругу;
• площадь прямоугольника – это сумма всех его сторон

4. Постановка проблемы урока: Готовясь к уроку, вырезала круги. Осталась бумага в форме прямоугольника со сторонами 15 см и 10 см. Хватит ли мне этой бумаги, чтобы вырезать круг радиусом 7 см ?

II. Изучение новой темы.

1. Работа в группах:

Группа 1 Задания:

1. Измерить длину каждой окружности нитью.
2. Измерить радиус каждой окружности.
3. Вычислить диаметр каждой окружности.
4. Разделить длину окружности на диаметр, округлив до сотых.
5. Какая получилась закономерность? Сформулировать вывод, ответив на вопрос: Почему отношение длины окружности к диаметру разных окружностей равно…..

Группа 2 Задания:

1. Отметить на окружности точку А.
2. Прокатить окружность по прямой линии от точки А до точки А.
3. Измерить длину полученного отрезка.
4. Аналогично то же самое проделать с двумя другими окружностями.
5. Измерить радиус каждой окружности.
6. Вычислить диаметр каждой окружности.
7. Разделить длину окружности на диаметр, округлив до сотых.
8. Какая получилась закономерность? Сформулировать вывод, ответив на вопрос: Почему отношение длины окружности к диаметру разных окружностей равно…..

Группа 3 Задания:

1. Начертить три окружности радиуса 1,5 см, 3 см, 4 см.
2. Сосчитать сколько квадратных сантиметров в каждом круге.
3. Вычислить квадрат радиуса каждого круга.
4. Разделить полученную площадь на квадрат радиуса, округлив до сотых.
5. Какая получилась закономерность? Сформулировать вывод, ответив на вопрос: Почему отношение площади круга к квадрату радиуса разных кругов равно…..

Группа 4 Задания:

1. Первый круг сложить так, чтобы получилась 4 равных сектора.
2. Второй круг сложить так, чтобы получилось 8 равных секторов.
3. Третий круг сложить так, чтобы получилось 16 равных секторов.
4. Вырезать по одному сектору из каждого круга.
5. Сравнить эти секторы. Сформулировать вывод, ответив на вопрос: Чем больше секторов получается из круга, тем ……... центральный угол, а также тем больше сектор похож на …..

Группа 5 Задания:

1. Разделить первый круг на сектора, у которых центральные углы по 90⁰.
2. Разделить второй круг на сектора, у которых центральные углы по 120⁰.
3. Разделить третий круг на сектора, у которых центральные углы по 45⁰.
4. 4. Ответить на вопрос:
   1. Сколько секторов получилось в каждом случае.
   2. На сколько секторов будет разделен круг, если у него центральные углы по 20 ⁰, по 12 ⁰?
   3. Какой будет центральный угол, если круг разделен на 15 равных секторов? на 72 равных сектора?

Выводы:

• 1, 2 и 3 групп – получено одно и то же число,
• 4 группы – сектор похож на треугольник,
• 5 группы - умение находить центральные углы по секторам и наоборот.

Таким образом, выводится формула С = π d = 2πr.

2. Учащимся предлагаются презентации для лучшего запоминания числаπ: Конкина Алексея, Андреевой Светланы, Шкиря Алеси, а также стихотворение о совах:

Двадцать две совы скучали

На больших сухих суках.

Двадцать две совы мечтали

О семи больших мышах,

О мышах довольно юрких,

В аккуратных серых шкурках.

Слюнки капали с усов

У огромных серых сов.

3. Вывод формулы S = πr² предлагается в виде презентации, сделанной учителем, по ходу которой учащиеся отвечают на вопросы:

• Сколько секторов получится, если центральный угол у каждого будет по 10 ⁰ ?
• Чем меньше центральный угол, тем больше сектор напоминает по форме ..……………?
• Таким образом, круг разделили на ….. секторов, которые мы рассматриваем как ………………..?

III. Закрепление новой темы.

Учащиеся выполняют:

1. № 383 – дети рассуждают о решениях Маши и Миши – прямая пропорциональность между диаметром (радиусом) и длиной окружности.

2. Мотивация - где находят применение указанные формулы?

№ 390 – измерить длину веревки колодца – С = π х 30=94,2 (см)

Глубина = 25 х 94,2=2355 (см).

3. Решение проблемы, поставленной в начале урока. Хватит ли мне этой бумаги в форме прямоугольника со сторонами 15 см и 10 см, чтобы вырезать круг диаметром 14 см ?

Решение: S = π х 49=153,86 (см). Ответ: не хватит.

IV. Итог урока:

• что узнали нового?
• выставление отметок,
• домашняя работа: № 388, № 399 – выявить прямую пропорциональность в формуле площади круга, выучить 2 формулы.