Одними из самых древних являются задачи на
равенство площадей (равновеликость), поскольку
как раз при измерении площадей в Египте и
зарождалась геометрия.
Историк Геродот (V век до н. э) писал: "Если Нил
заливал чей-нибудь участок, то пострадавший
обращался к царю и докладывал ему о случившемся.
Тогда царь посылал землемеров (геометров); они
измеряли, на сколько уменьшился участок и
сообразно этому уменьшали налог. Вот откуда
возникла геометрия (землемерие)”
В книгах "Начала” Евклида равновеликость
фигур означает, что они могут быть составлены из
частей. Именно этими средствами, не прибегая даже
к пропорциям, Евклид доказывает, что каждый
многоугольник может быть преобразован в
равновеликий (равносоставленный) треугольник, а
треугольник — в квадрат.
Рассмотрим простейшие случаи равенства
площадей
1. а || СВ. Все треугольники С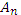 В равновелики (рис1)т.к. имеют
общее основание и высоту. В равновелики (рис1)т.к. имеют
общее основание и высоту.
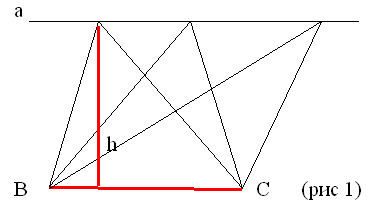
2. Медиана треугольника делит его на два
равновеликих треугольника (докажите)
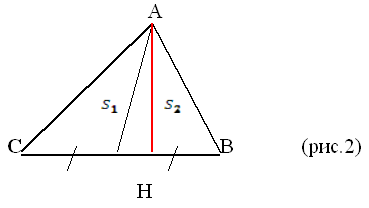
3. Диагонали параллелограмма делят его на 4
равновеликих треугольника
Доказательство: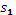 =
=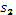 и и 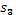 = =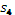 (имеют равные основания и общую высоту),
аналогично (имеют равные основания и общую высоту),
аналогично
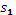 + +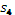 = =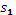 + +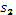 ,
следовательно: ,
следовательно: 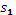 = =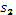 = = 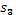 = =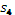
Решим задачи, используются свойства
равновеликости фигур
Задача 1 Дан параллелограмм АВСD и точка М
вне плоскости параллелограмма (рис 4) Проведите
через точку М прямую, делящую его на две
равновеликие фигуры
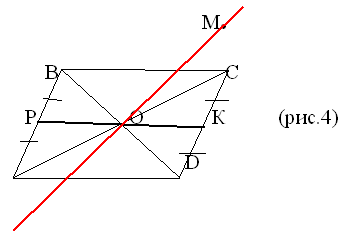
Решение: Проведем диагонали АС и ВD,
которые пересекутся в точке О.Прямая МО будет
искомой. Она разбивает параллелограмм на две
трапеции, у которых равные высоты и равные
средние линии РО = КО.
Задача 2. В параллелограмме АВСD
вырезали отверстие в виде прямоугольника.
Провести прямую так, чтобы разделить оставшуюся
часть на две равновеликие фигуры
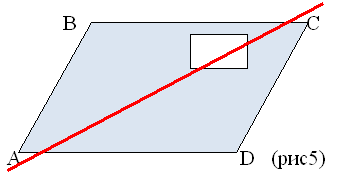
Решение: Проведем диагонали
параллелограмма и прямоугольника. Через точки
пересечения диагоналей О и М проведем прямую ОМ.
Данная прямая будет искомой (см. предыдущую
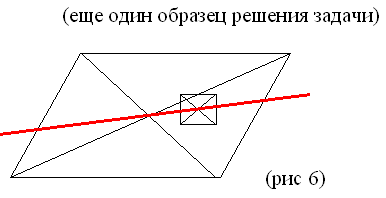
задачу) (еще один образец решения задачи)
Задача 3 Диагонали трапеции делят ее на 4
треугольника. Докажите, что треугольники,
прилегающие к боковым сторонам трапеции,
равновелики.
Решение 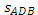 = =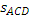 Если из равных
площадей отнять одну и туже площадь, то
оставшиеся площади будут равны. Если из равных
площадей отнять одну и туже площадь, то
оставшиеся площади будут равны. 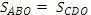
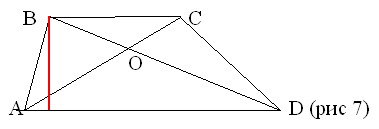
Задача 4 На основаниях ВС и АD
трапеции АВСD произвольно взяты точки М и К(рис 7)
МА и МD пересекаются с КВ и КС в точках Е и N
соответственно. Докажите, что площадь
четырехугольника ЕМNК равна сумме площадей
треугольников АВЕ и DNC
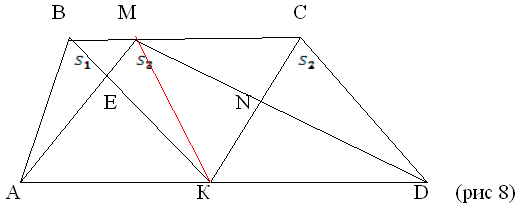
Решение. Обозначим площади треугольников
через 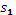 и и 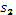 , четырехугольника - , четырехугольника -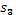 Соединим точки М и
К получим две трапеции АВМК и КМСD. Площади
треугольников, прилежащих к боковым сторонам
равны (доказано в задаче 3).Следовательно, Соединим точки М и
К получим две трапеции АВМК и КМСD. Площади
треугольников, прилежащих к боковым сторонам
равны (доказано в задаче 3).Следовательно, 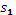 + + 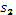 ,= ,=
Задача 5 В трапеции СD (рис9) ВК || СD, где К 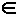 АС.
Докажите, что треугольники АВС и КСD равновелики АС.
Докажите, что треугольники АВС и КСD равновелики
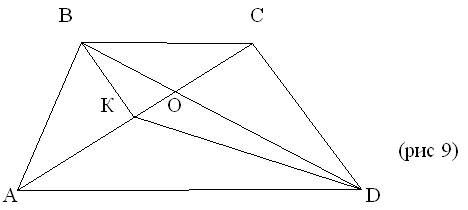
Решение В трапеции АВСD = (задача 3), в
трапеции KBCD 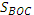 = =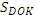 Сложим равные
площади, получим Сложим равные
площади, получим 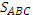 =
=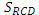 . .
Для нахождения площади произвольного
многоугольника его обычно разбивают на
треугольники и находят площадь каждого из них.
Сумма площадей этих треугольников равна площади
данного многоугольника. Площадь многоугольника
можно найти другими способами. Один из таких
способов был указан Евклидом. Он состоит в
построении треугольника равновеликого данному.
Рассмотрим пример.
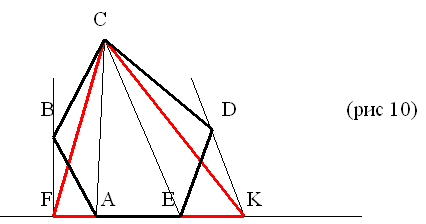
Дан выпуклый пятиугольник АВСDЕ построим
равновеликий ему треугольник. Для этого через
вершину В проведем прямую, параллельную
диагонали АС и через точку D прямую параллельную
диагонали СЕ (рис 10).
AFBC трапеция по построению следовательно 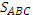 = = 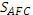 (общее основание АС и высота) (общее основание АС и высота)
Аналогично EKDC трапеция и 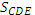 = =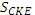 Таким образом =
Таким образом =
Применяя способ Евклида к трапеции, получаем
другой способ вывода площади трапеции.
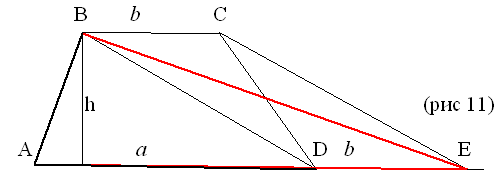
Рассмотрим трапецию АВСD с основаниями АD = а
и ВС = в и высотой h Проведем через вершину В
прямую СЕ || ВD , тогда 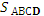 = Четырехугольник ВСЕD параллелограмм,
поэтому ЕD = ВС = в. Итак, = Четырехугольник ВСЕD параллелограмм,
поэтому ЕD = ВС = в. Итак, 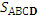 = (a +b)h = (a +b)h
Докажем еще одну формулу для площади трапеции
Доказать, что площадь трапеции равна
произведению боковой стороны и перпендикуляра,
проведенного из середины другой боковой стороны
к прямой содержащей первую сторону
Доказательство
Пусть в трапеции АВСD точка Е –середина СD, а
EF –перпендикуляр к АВ через точку Е(рис 12)
Проведем прямую, параллельную АВ и пересекающую
прямые АD и ВС в точках К и М соответственно. АМВК
– параллелограмм и 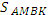 = FD · EF. Этот параллелограмм и трапеция АВСD
равносоставлены, следовательно, равновелики,
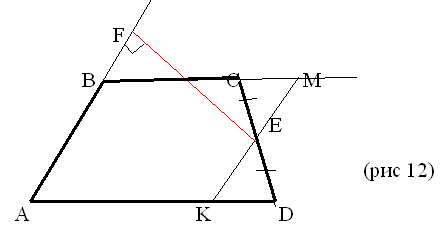
значит = FD · EF. Этот параллелограмм и трапеция АВСD
равносоставлены, следовательно, равновелики,
значит 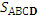 = AB · EF = AB · EF
| 
