Цели урока:
- дать представление о неизвестных учащимся
аксиомах геометрии, повторить уже известные им
аксиомы;
- ввести аксиому параллельных прямых;
- ввести понятие следствия из аксиом, теорем;
- показать как используются аксиома параллельных
прямых и следствия из неё при решении задач;
- воспитание патриотизма, гордости за свою родину
на примере великого русского математика
Н.И.Лобачевского.
Оборудование: компьютер, проектор.
ХОД УРОКА
1. Проверка предыдущего домашнего задания
2. Повторение уже известных учащимся аксиом
планиметрии
Учитель: В знаменитом сочинении
Евклида «Начала» (III в. до н.э.) были
систематизированы основные известные в то время
геометрические сведения. Главное же − в
«Началах» был развит аксиоматический подход к
построению геометрии, который состоит в том, что
сначала формулируются основные положения, не
требующие доказательства (аксиомы), а затем на их
основе посредством рассуждений доказываются
другие утверждения (теоремы). Некоторые из
аксиом, предложенных Евклидом, и сейчас
используются в курсах геометрии.
Само слово «аксиома» происходит от греческого
«аксиос», что означает «ценный, достойный».
Полный список аксиом планиметрии, принятых в
нашем курсе геометрии, приведён в приложениях в
конце учебника на страницах 344-348. Эти аксиомы вы
рассмотрите дома самостоятельно.
Некоторые из этих аксиом мы уже рассматривали.
Вспомните и сформулируйте эти аксиомы.
Учащиеся:
1) Имеются, по крайней мере, три точки, не лежащие
на одной прямой.
2) Через любые две точки проходит прямая, и притом
только одна.
3) Из трёх точек прямой одна и только одна лежит
между двумя другими.
4) Каждая точка О прямой разделяет её на две части
(два луча) так, что любые две точки одного и того
же луча лежат по одну сторону от точки О, а любые
две точки разных лучей лежат по разные стороны от
точки О.
5) Каждая прямая а разделяет плоскость на две
части (две полуплоскости) так, что любые две точки
одной и той же полуплоскости лежат по одну
сторону от прямой а, а любые две точки разных
полуплоскостей лежат по разные стороны от прямой
а.
6) Если при наложении совмещаются концы двух
отрезков, то совмещаются и сами отрезки.
7) На любом луче от его начала можно отложить
отрезок, равный данному, и притом только один.
8) От любого луча в заданную полуплоскость можно
отложить угол, равный данному неразвёрнутому
углу, и притом только один.
Учитель: Какие прямые называются
параллельными на плоскости?
Учащиеся: Две прямые на плоскости
называются параллельными, если они не
пересекаются.
Учитель: Сформулируйте признаки
параллельности прямых.
Учащиеся:
1) Если при пересечении двух прямых секущей
накрест лежащие углы равны, то прямые
параллельны.
2) Если при пересечении двух прямых секущей
соответственные углы равны, то прямые
параллельны.
3) Если при пересечении двух прямых секущей сумма
односторонних углов равна 180˚ то прямые
параллельны.
3. Новая тема. Аксиома параллельных прямых
Учитель: Решим задачу: «Через точку М,
не лежащую на прямой а, проведите прямую,
параллельную прямой а».
Решение.
План решения задачи обсуждается всем классом.
Один из учащихся записывает решение на доске (без
записи в тетрадях).

Учитель: Возникает вопрос: можно ли
через точку М провести ещё одну прямую,
параллельную прямой а?
Этот вопрос имеет большую историю. В «Началах»
Евклида содержится пятый постулат: «И если
прямая, падающая на две прямые, образуют
внутренние и по одну сторону углы, меньше двух
прямых, то продолженные эти прямые неограниченно
встретятся с той стороны, где углы меньше двух
прямых». Прокл в V в.н.э. переформулировал
постулат Евклида проще и понятнее: «Через точку,
не лежащую на данной прямой, проходит только одна
прямая, параллельная данной». Это и есть аксиома
параллельных прямых. Отсюда видно, что
рассмотренная выше задача имеет единственное
решение.
Многие математики предпринимали попытки
доказать пятый постулат, так как его
формулировка слишком напоминала теорему. Все эти
попытки каждый раз оказывались неудачными. И
лишь в XIX в. было окончательно выяснено, что пятый
постулат Евклида нельзя доказать, он сам
является аксиомой.
Огромную роль в решении этого вопроса сыграл
великий русский математик Николай Иванович
Лобачевский (1792-1856).
4. Смотрим презентацию о Н.И.Лобачевском
5. Закрепление изученного. Решение задач
№ 196
Дан ∆АВС. Сколько прямых, параллельных стороне
АВ, можно провести через вершину С?
Решение.
Согласно аксиоме параллельных прямых, можно
провести единственную прямую.
№ 197
Через точку, не лежащую на прямой р, проведены
четыре прямые. Сколько из этих прямых пересекают
прямую р? Рассмотрите все возможные случаи.
Решение.
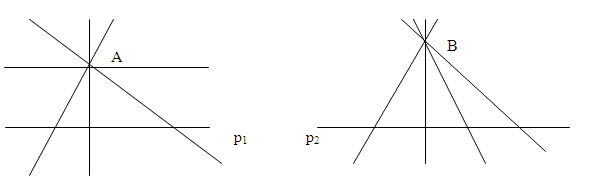
Ответ: 3 или 4 прямые.
Следствия из аксиомы параллельных прямых.
Утверждения, которые выводятся
непосредственно из аксиом или теорем, называются
следствиями. Рассмотрим следствия из аксиомы
параллельных прямых.
Следствие 1˚. Если прямая пересекает одну из
двух параллельных прямых, то она пересекает и
другую.

Следствие 2˚. Если две прямые параллельны
третьей прямой, то они параллельны. (Предлагается
доказать учащимся самостоятельно).
Чертёж тот же.
Дано: а || b, с || b
Доказать: а || с
Доказательство (метод «от противного»):
Пусть прямые а и с не параллельны. Тогда они
пересекаются в некоторой точке М. Через точку М
проходят две различные прямые (а и с),
параллельные прямой b. Это противоречит аксиоме
параллельных. Значит наше предположение не
верно. А верно то, что а || с. Ч.т.д.
Второе следствие из аксиомы параллельных прямых
является по сути дела ещё одним признаком
параллельности прямых на плоскости.
Решение задач: №№ 217 (устно), 218
(устно), 198, 200, 213.
№ 217 (устно)
Прямые а и b параллельны прямой с. Докажите, что
любая прямая, пересекающая прямую а, пересекает
также и прямую b.
Решение.
Если а || b и b || с, то а || с (следствие 2˚).
Если произвольная прямая d ∩ а, то d ∩ b (следствие 1˚).
№ 218 (устно)
Прямые а и b пересекаются. Можно ли провести
такую прямую, которая пересекает прямую а и
параллельна прямой b? Ответ обоснуйте.
Решение.
Возьмём на прямой а точку А 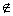 b. Через точку А можно провести
единственную прямую, параллельную прямой b
(аксиома параллельных). Построенная прямая будет
пересекать прямую а, так как имеет с ней общую
точку А. b. Через точку А можно провести
единственную прямую, параллельную прямой b
(аксиома параллельных). Построенная прямая будет
пересекать прямую а, так как имеет с ней общую
точку А.
№ 198
Прямые а и bперпендикулярны к прямой р, прямая с
пересекает прямую а. Пересекает ли прямая с
прямую b?
Дано: а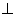 р, b р, b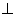 р, с ∩ а р, с ∩ а
Найти: пересекает ли с прямую b?
Решение: если а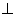 р и b р и b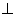 р, то а || b (теорема). р, то а || b (теорема).
Если с ∩ а и а || b, то с ∩ b (следствие 1˚).
Ответ: с ∩ b.
№ 200
На рисунке учебника АD || р и PQ || BC. Докажите, что
прямая р пересекает прямые АВ, АЕ, АС, ВС, РQ.

№ 213
На рисунке учебника СЕ = ED, ВЕ = EF и КЕ = AD.
Докажите, что КЕ || ВС.

6. Подведение итогов
1) В чём заключается главная заслуга Евклида?
2) Что называется аксиомой?
3) Какие аксиомы мы знаем?
4) Кто из русских учёных построил стройную теорию
неевклидовой геометрии?
5) Что называется следствием в математическом
смысле слова?
6) Какие следствия мы сегодня узнали?
7. Задание на дом:
§2, п.27, 28, приложение об аксиомах геометрии стр.
344-348, вопросы 7-11 стр. 68, №199, 214.
№199: Прямая р параллельна стороне АВ
треугольника АВС. Докажите, что прямые ВС и АС
пересекают прямую р.
№214: Прямая, проходящая через середину
биссектрисы AD треугольника АВС и
перпендикулярная к AD, пересекает сторону АС в
точке М. Докажите, что MD¦AB.
| 
