Продолжительность 45 мин.
1. Постановка проблемы.
Совету Геометров были предложены задачи по
нахождению площадей многоугольников. Они у них
вызвали большое затруднение. Не придя к единому
мнению, Геометры решили снарядить экспедиции на
остров Площадей, где по преданию находится ключ к
решению данных задач. Спонсировать данные
экспедиции будет (учитель называет себя ,
передаёт все события, произошедшие во время
плаванья на остров).
Целью данной экспедиции является поиск ключа,
при помощи которого можно будет решить задачи.
Вам предстоит сформировать две команды,
выбрать капитанов, придумать девиз, под которым
команды отправятся в путешествие.
(Даётся время на обдумывание).
В такое ответственное плаванье решила
отправиться команда . . . во главе с капитаном . . .,
девизом которой является . . . и команда…
2. Подготовка снаряжения.(Фронтальная
работа)
Учащимся раздаётся материал с заданием и
открывается соответствующий материал на доске.
Перед плаваньем все участники экспедиции
проверяют свою готовность: "Закрыли глаза,
вспомнили все формулы для нахождения площадей
многоугольников и привели свои мысли в порядок.
Открыли глаза и ответили на вопросы:
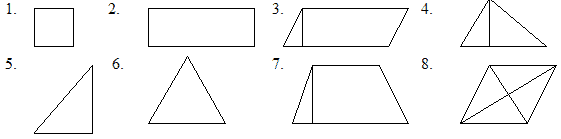
1. Назовите фигуру, изображённую на рисунке.
Найдите площадь каждой фигуры для приведённых
значений. Какие формулы для нахождения площади
вы использовали?
| 1. a) a= 1.2 cm |
2. а=2.5, b=4 |
3. a=8, h=1.25 |
4. a=20, h=15 |
6. a=b=5, c=6 |
| б) S=0.68 m2 |
5. a=4, b=3 |
7. a=20, b=4, h=5 |
8. d1=16, d2=12 |
|
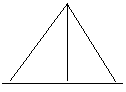
2. Найдите высоту треугольника по известной
боковой стороне и прилежащему углу.
3. Освобождение от притяжения Безымянного
острова.
(Объяснение новой темы. Работа у доски.)
Путешествие наших смельчаков длилось недолго.
На их пути встретился Безымянный остров,
обладающий свойством притягивать корабли. Для
преодоления его притяжения необходимо найти
площади треугольника и параллелограмма по двум
смежным сторонам и углу между ними.
Два смельчака(по одному от команды) выходят и
выводят формулы: S=absin?/2 , S=absin?.
4. Преодоление неожиданного препятствия.
Ровно три дня и три ночи плыли путешественники,
и вдруг их корабль неожиданно сел на мель. Для
преодоления этого препятствия необходимо
сказать волшебные слова, а именно вспомнить
формулы для нахождения площадей параллелограмма
и прямоугольника через диагонали и угол между
ними. К доске вызываются два ученика от каждой
команды. Они работают вместе с классом, делают
соответствующие рисунки и оформляют
соответствующие записи.
5. Пополнение запасов воды и
продовольствия.
Путь наших отважных путешественников
продолжается. Они видят скалистый остров, где
можно пополнить запасы продовольствия и воды.
Платой является создание алгоритма решения
задач по нахождению площадей многоугольников
через их две смежные стороны и углу между ними
(через две диагонали и углу между ними). Блок
схема должна быть правильно составлена каждым
членом команды.
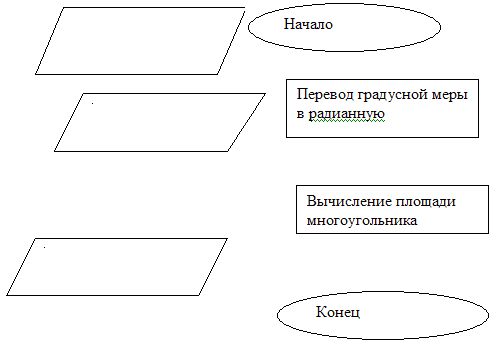
Сбор блок схемы по элементам.
6. Миражи. (Установление истинности
или ложности высказываний )
Глаза закрыты. Высказывание верно - руки вперёд,
ложно - вверх.
Верно ли, что:
- площадь прямоугольного треугольника равна
произведению его катетов?
- ромб – это параллелограмм, у которого стороны
равны?
- Площадь квадрата равна произведению его
смежных сторон?
- Площадь трапеции равна сумме оснований на
высоту?
- площадь ромба равна произведению двух сторон на
синус угла между ними?
- Площадь прямоугольника равна сумме всех его
сторон?
- Площадь треугольника равна половине
произведения его основания на высоту?
В результате слаженных действий команд, миражи
исчезли, и появился остров Площадей.
7. Поиск ключа. (Составление
программы и реализация её на компьютере).
Выбор задач осуществляется учеником из
предложенного списка.
8. Возвращение домой. (Подведение
итогов).
Для возвращения домой отважным
путешественникам необходимо ответить на
следующие вопросы:
"Ответив правильно на поставленные вопросы, вы
узнаете фамилию швейцарского учёного, который в
1968 году разработал первую версию языка
программирования Паскаль.” (Никлаус Вирт).
1. Автор бессмертного произведения "Начала”,
изданного более 2000 лет назад, живший в III веке до
нашей эры. (Евклид).
2. Величайший математик Сиракуз (287 –212г.г.). (Архимед).
3. Древнегреческий математик, живший в 3 веке до
н. эры. Его именем названа формула для нахождения
площади треугольника. (Герон).
4. Его именем называют клятву, которую дают
врачи. Он исследовал площади плоских фигур,
ограниченных прямыми линиями и дугами. (Гиппократ).
Итоги подводятся в командном первенстве и в
личном зачёте.
Задачи к этапу "Поиск ключа.”
Выберите задачу для решения. Напишите
программу для решения задачи и выполните её при
указанных значениях переменных.
1. Найдите площадь треугольника по его смежным
сторонам и углу между ними.
Решите задачу для
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
2. Найдите площадь параллелограмма по его
смежным сторонам и углу между ними.
Решите задачу для
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
3. Найдите площадь параллелограмма по его
диагоналям и углу между ними.
Решите задачу для
| d1 = 6; |
4,8; |
43,21. |
d2 = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
4. Найдите площадь прямоугольника по его
диагоналям и углу между ними.
Решите задачу для
| d1 = 6; |
4,8; |
43,21. |
| a = 300; |
480; |
1030. |
5. **Найдите высоту треугольника, опущенную на
сторону а, если его смежные стороны и угол между
ними равны соответственно:
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
6. **Найдите высоту треугольника, опущенную на
сторону b, если его смежные стороны и угол между
ними равны соответственно:
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
7. **Найдите высоту параллелограмма, опущенную
на сторону а, если его смежные стороны и угол
между ними равны соответственно:
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
8. **Найдите высоту параллелограмма, опущенную
на сторону b, если его смежные стороны и угол
между ними равны соответственно:
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480 |
1030. |
|
|
|
9. **Найдите одну из сторон прямоугольника,
площадь которого равна площади параллелограмма
и сторона в 2 раза больше стороны параллелограмма
, у которого смежные стороны и угол между ними
равны соответственно:
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
10. **Найдите сторону квадрата, равновеликого с
параллелограммом, у которого смежные стороны и
угол между ними равны соответственно:
| a = 6; |
4,8; |
43,21. |
b = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
|
11. **Найдите диагональ ромба, если его сторона а,
и угол между сторонами ?, а другая диагональ равна
d1.
Решите задачу для
| a = 6; |
4,8; |
43,21. |
d1 = 8; |
7,6; |
24,47. |
| a = 300; |
480; |
1030. |
|
|
| 
