Согласно месту урока в системе уроков отведенных
на изучение этой темы мной были поставлены
следующие цели:
- Научить учащихся применять определение,
свойства и признаки равнобедренного
треугольника к решению задач;
- Развитие мышления учащихся, познавательной
активности, интереса к предмету, творческих
способностей, умения применять имеющиеся знания
в новой ситуации;
- Воспитывать умение работать в команде, чувство
ответственности каждого за конечный результат
работы всей команды, чувство взаимовыручки,
культуру умственного труда.
Поставленные цели я постаралась реализовать
через все учебно-воспитательные этапы урока.
- Организационный момент имел целью настроить
ребят на быструю, четкую, продуктивную работу.
- Учебно-воспитательная задача второго этапа
была проверить усвоение пройденного, устранить
пробелы подготовить к восприятию задач,
предложенных на уроке. Репродуктивный метод
должен был помочь быстро проверить
сформированность умений и навыков,
отрабатывающихся при первичном закреплении
изучаемого материала. Детям, имеющим хороший
уровень познавательной активности была
предоставлена возможность проявить себя при
самостоятельном доказательстве теорем.
- Следующий этап урока: решение задач должен был
непосредственно работать на конечный результат
урока. На развитие и закрепление знаний, умений и
навыков по применению определения, свойств и
признаков равнобедренного треугольника. Для
реализации этих задач были выбраны различные
методы обучения: репродуктивный, частично
поисковый, который должен был способствовать
развитию умения сопоставлять, анализировать,
обобщать.
Для того, чтобы каждый ребенок имел возможность
проверить умения по применению своих знаний,
проведена небольшая самостоятельная работа с
применением опорного конспекта. Последующая
проверка способствовала выявлению пробелов и
очень хочется надеяться, что и их ликвидации. - Задача четвертого заключительного этапа урока
–подвести его итог, оценить работу учащихся,
нацелить на дальнейшее осознанное изучение
геометрии.
Я хотела и старалась сделать так, чтобы
структура урока была подчинена триединой цели
урока и достижению конечного результата. Я
старалась сделать так, чтобы для каждого ученика
была создана ситуация успеха, чтобы каждый
ученик был включен в поиск решения проблемы, а
значит в активную познавательную деятельность.
Урок – КВН по теме: "Равнобедренный
треугольник”
I)
- 1 конкурс. Представление команд (участвуют 3
команды).
Команды объявляют свое название и девиз.
Капитаны разыгрывают право первого хода.
Команды по очереди решают устные задачи по
готовым чертежам (Приложение 1 – презентация).
- 3 конкурс. Догони лидера.
Командам раздаются карточки с задачами.
Команда, которая первая решила и оформила
решение задачи, демонстрирует ее решение через
документ– камеру. Команда соперница проверяет
решение. Если необходимо, находит и исправляет
ошибки, задает вопросы по ходу решения.
Карточка:
№1 (2 балла) В равнобедренном треугольнике
угол, противолежащий основанию равен 1000.
Найдите углы при основании.
№2 (3 балла) Периметр равнобедренного
треугольника равен 36 см, основание на 3см меньше
боковой стороны. Найдите боковую сторону этого
треугольника.
№3 (4 балла) Один из углов при основании
равнобедренного треугольника равен 300.
Найдите угол, который образует с боковой
стороной медиана, проведенная к основанию.
Командам раздаются 2 комплекта карточек. На
карточках первого комплекта написаны словесные
формулировками определения, свойств и признаков
равнобедренного треугольника. На карточках
второго комплекта выполнены чертежи и краткие
записи этих определений и теорем. Команды должны
на доске с помощью магнитов составить
соответствующие пары.
II)
- 5 конкурс. Конкурс капитанов (домашнее задание).
Капитаны дома подготовили доказательство
одного из признаков равнобедренного
треугольника:
- Если в треугольнике медиана является высотой,
то треугольник – равнобедренный.
- Если в треугольнике медиана является
биссектрисой, то треугольник – равнобедренный.
- Если в треугольнике биссектриса является
высотой, то треугольник –равнобедренный.
III)
- 6 конкурс. Применим знания.
Команда, которая первая решила и оформила
решение задачи, демонстрирует ее решение через
документ– камеру. Команда соперница проверяет
решение. Если необходимо, находит и исправляет
ошибки, задает вопросы по ходу решения.
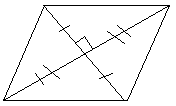
Задача: Докажите, что все стороны
четырехугольника равны.
- 7 конкурс "Дырявая” задача (индивидуальные
задания для каждого учащегося).
Детям выдаются бланки с условием и решением
задачи. В решении есть "дырки”, которые учащиеся
должны заполнить. Предложено две задачи разного
уровня сложности. Каждый ученик сам выбирает
себе задачу. Дети предупреждены, что оценка
каждого принесет баллы в копилку команды.
№1 (5 баллов)
Решите "дырявую” задачу
Дано:  MEN – равнобедренный;
[MN] – основание;
AN = BM.
Доказать: АВЕ – равнобедренный.
Доказательство:
- Рассмотрим MЕN:
по определению равнобедренного треугольника
…=…,
по свойству углов при основании равнобедренного
треугольника … = … - Угол ЕМN и угол ЕМА – …,
угол ЕNМ и угол ЕNВ – …,
углы ЕМN и ЕNМ равны (из п.1), значит, угол
ЕМА … углу ЕNВ. - АМ = АВ – МВ,
BN = АВ – …,
АN =ВМ (из …), значит, АМ … NB. - Рассмотрим АЕМ и ВЕN:
а) ЕМ = … (из п. 1),
б) … = NВ (из п. 3),
в) угол АМЕ = … (из п.2)
АЕМ
= ВЕN (по
…),
значит, АЕ= ВЕ (по…). - Рассмотрим АЕВ: ВЕ=… (из п.4), значит АВЕ –
равнобедренный (по …).
№2 (3 балла)
Дано: угол АВД = углу СВА, АВ = ВС.
Доказать: АДС – равнобедренный.
Доказательство:
1) Рассмотрим АВД и СВД:
а) угол АВД =…(из …),
б) … = ВС (из...),
IV)
Пока ученики решают задачи жюри (учителя
математики школы) подводит предварительные
итоги игры. Окончательные итоги будут объявлены
на следующем уроке после проверки
индивидуальной работы учащихся. За урок получают
оценки капитаны команд и учащиеся наиболее ярко
проявившие себя во время урока. Домашнее задание: §10 (учебник И.М. Смирновой
и В.А. Смирнова); задача на карточке.
|
