Цели урока:
- Образовательные: повторение теоретических
сведений по теме; рассмотрение правил
треугольника и параллелограмма сложения
векторов в пространстве, законы сложения
векторов; изучение правил сложения нескольких
векторов в пространстве и его применение при
нахождении векторных сумм, не прибегая к
рисункам; рассмотрение правил умножения вектора
на число и основные свойства этого действия, а
так же их применение при решении задач.
- Развивающие: развитие памяти,
математической речи, наблюдательности, развитие
графических навыков у учащихся.
- Воспитательные: формирование культуры
ученического труда.
Тип урока: урок изучения нового
материала
ХОД УРОКА
1. Организационный момент
Сообщение темы и цели урока
Учитель: Ребята, тема нашего урока
«Действия над векторами». Сегодня
мы рассмотрим правила треугольника и
параллелограмма сложения векторов в
пространстве; изучим правило сложения
нескольких векторов в пространстве и его
применение при нахождении векторных сумм, не
прибегая к рисункам; рассмотрим правила
умножения вектора на число и основные свойства
этого действия, а так же их применение при
решении задач.
2. Актуализация знаний (Устная
работа)
Учащиеся отвечают на вопросы учителя. Если
учащиеся затрудняются ответить, учитель
помогает.
Учитель: 1вопрос. Что называется
вектором в пространстве? Его обозначения.
Ученик: Отрезок, для которого указано,
какой из его концов считается началом, а какой
концом, называется вектором.
Учитель: 2 вопрос. Что называется
длиной вектора? Ее обозначение.
Ученик: Длиной ненулевого вектора называется
длина отрезка АВ.
Учитель: 3 вопрос. Какой вектор
называется нулевым?
Ученик: Любая точка пространства
может рассматриваться как вектор. Такой вектор
называется нулевым.
Учитель: 4 вопрос. Какие
векторы называются коллинеарными?
Ученик: Два ненулевых вектора
называются коллинеарными, если они
лежат на одной прямой или на параллельных прямых. Учитель: 7 вопрос. Каким
(сонаправленным или противоположно
направленным) принять нулевой вектор?
Ученик: Нулевой вектор принято
считать сонаправленным с любым вектором.
3. Изучение нового материала
Задача учителя подчеркнуть, что сложение и
вычитание векторов в пространстве вводится так
же, как и на плоскости, и подчиняется тем же
законам. Раздать опорную схему по теме и дать
время для работы над конспектом в тетради. Учащиеся делают записи в тетрадях.
Учитель просит учащихся записать законы в
тетрадь.
Учитель: Сформулируем правило
многоугольника. Сложение нескольких векторов в
пространстве выполняется так же, как и на
плоскости: первый вектор складывается со вторым,
затем их сумма — с третьим вектором и т. д. Из
законов сложения векторов следует, что сумма
нескольких векторов не зависит от того, в каком
порядке они складываются. 
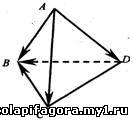
Задача.
Дан тетраэдр АВСД. Найдите сумму:
а) 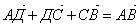
б) 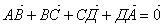
в) 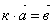
Если 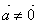 , , 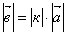 то, то,  при при 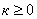 ; ;
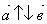 при
при 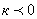 . .
Если 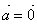 , то , то 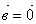 . .
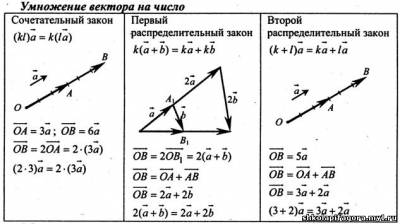
Рассмотреть законы умножения вектора на
число и попросить ребят изобразить схему в
тетрадях.
6. Закрепление изученного материала (выполнение
задач)
Учащиеся выполняют № 345: один учащийся у
доски, учитель комментирует
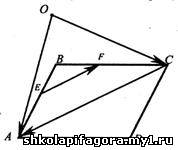
№
345. Точки E и F – середины сторон АВ
и ВС параллелограмма АВСД, а О –
точка произвольная точка пространства. Выразите
вектор 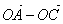 через
вектор через
вектор 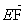 . .
Решение: 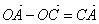
Так как EF – средняя линия треугольника АВС,
EF|| АС и EF = 1/2 АС.
Поэтому 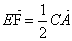 , , 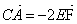 , , 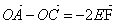
№ 347. Упростить выражение:
а) 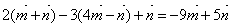
7. Домашнее задание (с комментарием
учителя)
§ 2 (п. 36, 37, 38), № 335, № 337 (а, б), № 347 (б).
8. Подведение итогов урока
В конце урока желательно с помощью ребят
перечислить понятия, правила, свойства, которые
были рассмотрены на уроке и которые необходимо
запомнить. Выставление оценок.
Учитель: Давайте подведем итоги урока.
Блиц-опрос по вопросам:
– Что называется произведением ненулевого
вектора на число?
– Что называется произведением нулевого вектора
на число?
– Свойства умножения вектора на число.
– Справедливо ли утверждение:
а) любые два противоположно направленных
вектора коллинеарны;
б) любые два вектора коллинеарных противоположно
направленны;
в) любые два равных вектора коллинеарны;
г) любые два сонаправленных вектора равны?
| 
