Цели:
- Дать учащимся начальное представление о графическом решении уравнений с
параметрами.
- Обучать учащихся с помощью графиков функций определять количество решений
уравнений, содержащих параметр.
- Воспитывать интерес к предмету математики.
Оборудование:
- мультимедийное оборудование
- материалы к уроку
Организация урока:
- Посадка учащихся – традиционно.
- У каждого на столе индивидуальные рабочие тетради.
- Урок сопровождает презентация.
Ход урока
1 этап
Учитель объявляет тему урока. Подчеркивается значимость темы. В
контрольно-измерительных материалах единого государственного экзамена задачи С5
рассчитаны на учащихся, владеющих навыками работы с параметром.
Научить учащихся решать задачи с параметром за один год сложно, необходимо
готовиться серьезно и поэтапно, начиная с простейших задач с параметрами.
В данный момент рассматриваются простейшие уравнения с параметром, их
графические иллюстрации.
Что значит решить уравнение? (Найти такие значения переменной, при которых
уравнение превращается в верное числовое равенство, иначе, когда числовое
значение левой части равно числовому значению правой).
Например, 2х + 3 = 7. Какое число является его решением? ( х=2)
На экране графики двух функций (рисунок 1) у = х2 + 1 и у
= 2/х.
Есть ли у них общая точка? (У этих графиков есть одна общая точка (1;
2)).
Как ответить на вопрос: «Какое значение х является решением уравнения х2
+ 1 = 2/х?» (х = 1)
На экране рисунок 2.
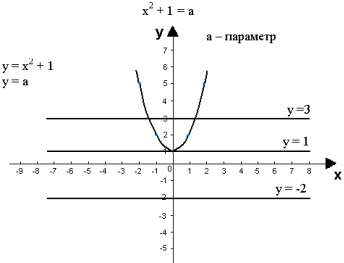
Что является графиком функции у = х2 + 1? (Парабола у = х2,
смещенная вверх на одну единицу).
Что является графиком функции у = а? (Прямая, параллельная оси Ох)
Сколько решений, в зависимости от параметра а, имеет уравнение х2
+ 1 = а?
(Если а < 0, прямая у = а не пересекает график у = х2 + 1;
если 0 ≤ а < 1 прямая у = а не пересекает параболу.
Если а = 1 парабола и прямая имеют единственную точку пересечения, т.е. исходное
уравнение имеет единственное решение;
при а > 1 таких точек пересечения две).
Учитель: При решении задач с параметрами очень важно грамотно записать
ответ.
Ответ:
при а < 1 – корней нет,
при а = 1 – единственный корень,
при а > 1 – два корня.
Рассматривается уравнение |х2 – 2| = а
Как построить график левой части уравнения? (Строим параболу у = х2,
переносим вниз вдоль оси Оу на 2 единицы вниз. Верхнюю часть оставляем без
изменений, а нижнюю часть симметрично отображаем относительно оси Ох).
Сколько решений имеет уравнение |х2 – 2| = а в зависимости от
параметра?
На экране рисунок 3.
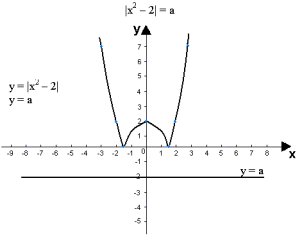
(При а < 0 – решений нет, при а = 0 – 2 решения, при 0 < а < 2 – 4 решения,
при а = 2 – 3 решения, при а > 2 – 2 решения).
Далее учащиеся работают письменно.
При каждом значении параметра а определить количество решений уравнения |х| +
|х – 4| = а.
Строим график функции у = |х| + |х – 4|
Как выполняются построения? (Находим нули подмодульных выражений, отмечаем
их на прямой, рассматриваем знаки переменной х на каждом из получившихся
промежутков. Далее, в зависимости от знака х и х – 4, записываем какой вид имеет
функция. Строим получившиеся линии).
Учащиеся строят график в тетрадях, на экране показывается рисунок 4.
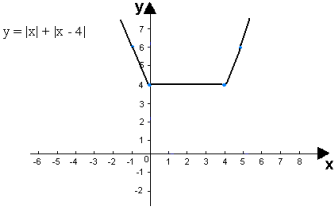
Как записать ответ к данной задаче? (При а < 4 – решений нет, при а = 4 –
бесчисленное множество решений, при а > 4 – два решения).
Ответ записывается на доске и в тетрадях.
Построим график функции y = |х – 1| + |х – 3| – 2|х|.
Аналогично предыдущему заданию учащиеся расписывают поэтапно поведение
функции на каждом из промежутков, строят график. Теперь рассмотрим задачу: определить количество решений уравнения |х – 1| +
|х – 3| – 2|х| = а в зависимости от параметра а.
Каждый учащийся самостоятельно записывает ответ к задаче.
(При а – 4 и а = -4 – решений бесчисленное множество;
при -4 < а < 4 – единственное решение;
при а < -4, а > 4 – решений нет).
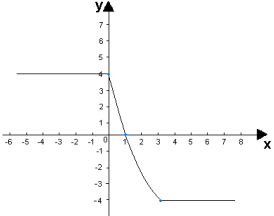
Далее рассматривается уравнение, где правая часть имеет иной вид |х| = х + а
Что является графиком функции у = х + а?
(у = х – прямая, которая является биссектрисой 1 и 3 координатных углов;
у = х + а – прямая, параллельная у = х при а ≠ 0.
При а > 0 – прямая двигается вверх;
при а < 0 – прямая двигается вниз).
Строим графики функций у = |х| и у = х
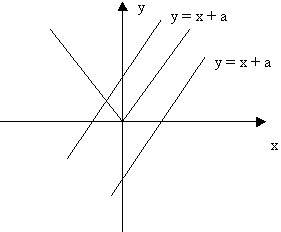
Получаем ответ:
При а < 0 – решений нет;
при а = 0 – бесчисленное множество решений;
при а > 0 – единственное решение.
Мы познакомились с простейшими уравнениями, содержащими параметр, научились
определять количество решений в зависимости от параметра.
В дальнейшей работе мы будем усложнять задачи, содержащие параметр.
| 
