Цель: приобретение базовых знаний в области фундаментального раздела математики "Линейная алгебра”. Проверка
усвоения знаний по вычислению обратной матрицы, нахождению
алгебраических дополнений, дополнительного минора, вычислению
определителей, решению матричных уравнений.
Задачи:
- развитие творческого профессионального мышления;
- развитие познавательной мотивации;
- овладение языком науки, приобретение навыков оперирования понятиями;
- овладение умениями и навыками постановки и решения задач;
- углубление теоретической и практической подготовки;
- развитие инициативы и самостоятельности студентов;
- формирование общих компетенций:
– организация собственной деятельности, исходя из цели и способов ее достижения, определенных руководителем;
– анализ рабочей ситуации, осуществление текущего и итогового контроля,
оценка и коррекция собственной деятельности, ответственность за
результаты своей работы;
– осуществление поиска информации, необходимой для эффективного выполнения профессиональных задач;
– использование информационно-коммуникационных технологий в профессиональной деятельности;
– работа в команде, эффективное общение с коллегами, руководством.
Обеспечение практического занятия:
Теоретический материал методической рекомендации к практической работе.
Учебники: Богомолов Н.В. "Математика”. – М.: Дрофа, 2009.
Омельченко В.П., Э.В. Курбатова. Математика, – Серия: Среднее профессиональное образование. – Ростов-на-Дону "Феникс”,2008-380с.
Индивидуальные карточки с вариантом практической работы.
Структура практического занятия.
1. Организационный этап.
Проверка готовности обучающихся к занятию.
2. Этап подготовки обучающихся к активному усвоению нового материала.
3. Этап усвоения новых знаний.
Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины.
Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
- Изучение теоретического материала по теме "Матричные уравнения. Вычисление обратной матрицы”.
4. Этап проверки понимания обучающимися нового материала.
- Примеры решения типовых заданий.
5. Этап закрепления нового материала.
- Выполнение практической работы по вычислению определителей, выполнению действий над матрицами, решению матричных уравнений.
6. Итоги занятия. Рефлексия.
7. Этап информирования обучающихся о домашнем задании.
Теоретические сведения и методические рекомендации по решению задач.
1. Изложение теоретического материала.
Определение. Квадратная матрица A-1 называется обратной к квадратной матрице
A того же порядка, если
AA-1 = A-1A = E , где
E – единичная матрица.
Утверждение. Квадратная матрица A
имеет обратную матрицу тогда и только тогда, когда
det A≠ 0 .
Утверждение. Элементы cij обратной матрицы
A-1 , если она существует, можно найти по формуле
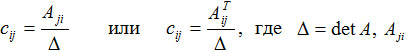– алгебраическое дополнение к элементу
aij матрицы
A, ATij – алгебраическое дополнение к элементу
aTij транспонированной матрицы
AT.
Определение. Алгебраическим дополнение
Aij элемента
aij называется число, равное
Aij = (–1)i+jMij.
Определение. Дополнительным минором
Mij элемента
aij матрицы
Ann называется определитель матрицы n-1-го порядка, полученный из матрицы
Ann вычеркиванием i-ой строки и j-го столбца.
Однако, такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:
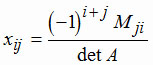 , где Мji
дополнительный минор элемента аji матрицы А.
Значение определителя: -10 + 6 – 40 = -44.
2. Закрепление теоретического материала, решение типовых задач.
№ 1. Найти матрицу
C = A-1
обратную к A, если
 .
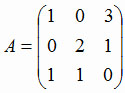Решение. Прежде всего вычислим определитель матрицы
A, чтобы убедиться в возможности существования обратной матрицы.
 
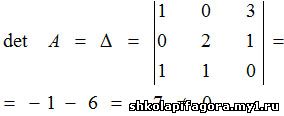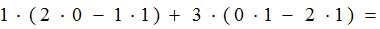
Следовательно, для матрицы A существует обратная матрица.
Воспользуемся формулой, выражающей элементы обратной матрицы через
алгебраические дополнения к элементам транспонированной матрицы.
Для AT имеем
 .
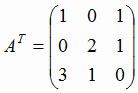Вычислим последовательно элементы Cij :
С учетом полученных данных, обратная к A матрица имеет вид
 №
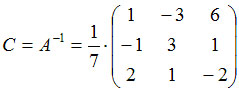2.
Решить матричное уравнение A
· X = B, где
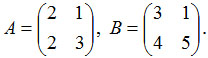
Решение. Такое матричное уравнение, если определитель матрицы
A отличен от нуля, удобно решать путем умножения обеих частей уравнения слева на матрицу
A-1 . В этом случае для искомой матрицы получим
A-1 · A · X = A-1 · B
и поскольку A-1
· A = E, то
X = A-1 · B.
Найдем теперь выражение для A-1 . Детерминант
Δ матрицы
A равен 4. Пользуясь формулами, определяющими элементы обратной матрицы, имеем
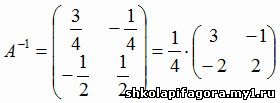 . Учитывая последнее, для X
получим:
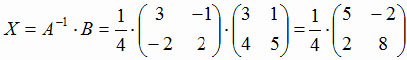 . 3. Практическая работа обучающихся.
|
Вариант 1
1.
Найти матрицу обратную данной:
|
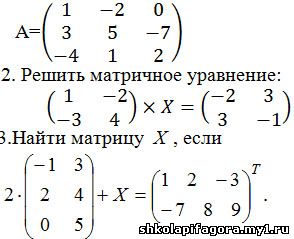
Вариант 2
1.
Найти матрицу обратную данной:
|
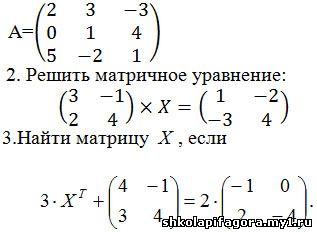
4. Подведение итогов практического занятия.
Рефлексия.
О чем сегодня на занятии шла речь?
Что было новым?
С какими трудностями Вы столкнулись?
Контрольные вопросы:
1. Сформулировать свойства определителя.
2. Какую матрицу называют обратной?
3. При каком условии существует обратная матрица?
4. Что называется алгебраическим дополнением матрицы?
5. Что называется минором матрицы?
6. В чем заключается метод построения обратной матрицы с использованием алгебраических дополнений.
5. Домашнее задание.
Учить определения, составить опорную схему конспекта. Выполнить упражнения:
1. Какая из матриц
B, C, D является обратной к матрице
A, если:
2. При каких λ существует
A-1, если:
3. Найти матрицу, обратную данной, если она существует:
| 
