- познакомить с методами решения уравнений,
содержащих под знаком модуля выражение с
переменной;
- формирование умения решать данные уравнения,
научить выбирать наиболее рациональный метод
решения уравнений;
- развитие логического мышления, речи;
- создание условий, способствующих воспитанию у
учащихся внимательности и аккуратности в
решении уравнения.
Методы обучения: объяснение, выполнение
тренировочных упражнений.
Формы контроля: самопроверка самостоятельно
решенных задач.
Оборудование: компьютер, мультимедийный
проектор, экран, папка с файлами (практикум),
презентация урока (слайды).
Ход занятия
Фронтальный опрос.
Сформулируйте определение модуля числа.
Сформулируйте геометрическое истолкование
модуля.
Может ли быть отрицательным значение суммы 2+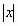 ? ?
Может ли равняться нулю значение разности 2-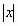 ? ?
Как сравниваются два отрицательных числа?
Устная работа. Раскрыть модуль:
1. 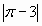 ; ; |
6. 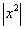 ; ; |
2. 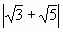 ; ; |
7. 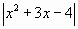 ; ; |
3. 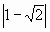 ; ; |
8. 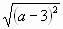 при при 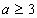 ; ; |
4. 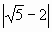 ; ; |
9. 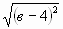 при при 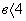 ; ; |
5. 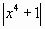 ; ; |
10. 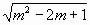 при при 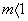 . . |
Проверка домашнего задания (класс разбит на 6
групп, каждая группа готовила презентацию по
заранее выбранному методу, которая и будет
представлять, и защищать ее).
Изучение нового материала.
1. Метод интервалов
Для того, чтобы решить уравнение, содержащее
неизвестную под знаком модуля, необходимо
освободиться от знака модуля, используя его
определение. Для этого следует:
1) Найти критические точки, т.е. значение
неизвестной, при которых выражение, стоящее под
знаком модуля, обращается в нуль;
2) Разбить область допустимых значений
уравнения на промежутки, на каждом из которых,
выражения, стоящие под знаком модуля сохраняют
знак;
3) На каждом из этих промежутков уравнение
записать без знака модуля, а затем решить его.
Объединение решений, найденных на всех
промежутках, и составляет решение исходного
уравнения.
Пример 1. Решите уравнение: |x+4|=2x -10.
Ответ: 14.
Пример 2. Решите уравнение: х 2-5|x|+6=0
Ответ: +-2; +-3.
Пример 3. Решите уравнение: |5-2x|+|x+3|=2-3x
5-2x=0 x+3=0
х=2,5 х=-3
| |
(- 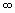 ;-3) ;-3) |
[-3;+2,5) |
[-2,5;+ 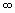 ) ) |
| 5-2х |
+ |
+ |
- |
| х+3 |
- |
+ |
+ |
(- 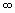 ;-3) ;-3) |
[-3;+2,5) |
[-2,5;+ 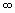 )
) |
| 5-2х-х-3-2+3х=0 0х=0
х-любое число
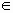 (- (- 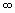 ;-3) ;-3)
|
5-2x+x+3-2+3x=0 2х=-6
х=-3 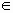 [-3;2,5) [-3;2,5) |
2х-5+х+3-2+3х=0 6х=4
x=2/3 [2,5;+ 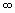 ) ) |
(- 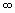 ;-3) v {-3}=(- ;-3) v {-3}=(- 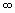 ;-3] ;-3]
Ответ: (- 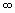 ;-3]. ;-3].
2. Возведение обеих частей уравнения в квадрат.
Для того, чтобы решить уравнение содержащее
модуль, необходимо освободиться от знака модуля.
Для этого следует: возвести в квадрат обе части
уравнения, решить его. Но не забывать, что при
возведении в квадрат появляются лишние корни,
поэтому, надо найти ОДЗ и выявить принадлежат ли
корни данному условию.
Пример 4. Решите уравнение: |x+4|=2x-10.
Возведем в квадрат обе части уравнения
X2 +8x+16=4x2 -40x+100
3x2 -48x+84=0 /3
X2 -16x+28=0
X1=14, X2=2
Найдём ОДЗ:
2x-10>0;
2x>10 ;
x>5.
x1=14 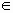 [5;+ [5;+ 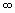 ), х2=2 [5;+ ), х2=2 [5;+ 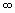 ) )
Ответ:14
Пример 5. Решите уравнение: |x+3|=2x-3
Возведем в квадрат обе части уравнения
х2 +6x+9=4x2 -12x+9; 3x2 -18x=0 /:3
х2 -6x=0; x(x-6)=0
x=0, x=6.
Найдём ОДЗ: 2х-3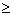 0, 2x 0, 2x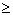 3,
x 3,
x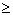 1,5 1,5
x=0 [1,5;+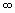 ) )
x=6 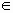 [1,5;+ [1,5;+ 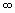 ) )
Ответ: 6.
3. Метод введения новой переменной
Иногда уравнение, содержащее переменную под
знаком модуля, можно решить довольно просто,
используя метод введения новой переменной.
Продемонстрируем данный метод на конкретных
примерах:
Пример 6. Решите уравнение: х2 -5|x|+6=0.
Пусть |x |=t,тогда
|x|2 =x2 =t2 ,тогда уравнение
примет вид:
t2 -5t+6=0
t1=2, |x |=2, x1,2= +- 2,
t2=3, |x |=3, x3,4=+- 3.
Ответ: +- 2, +- 3.
| 
