"Числа и геометрические тела
и фигуры... не являются достоянием одной лишь
математики;
в них выражается мировая гармония,
они имеют определенные магические
и
нравственные значения”.
(А.Я. Гуревич)
Цель урока: Обобщить изученный материал по
теме "Дроби”, показать, как на основе полученных
знаний можно провести соответствующие
исследования и подойти к созданию
учебно-исследовательской работы по изучению
возникновения дробных чисел, их символического
значения, роли дробного числа в жизни.
Оборудование: таблицы, учебники, планшет.
1. Введение в тему.
2. Проверка знаний учащихся и подведение их к
созданию проекта.
Ход урока
1. Фронтальный опрос учащихся
Учитель: Ребята, мы завершаем изучение
большой темы "Дробные числа. Все действия с
дробными числами”. Далее нас ожидает другая
глава "Отрицательные числа”. Сегодня мы
проведем необычный урок – урок подготовка к
исследовательской работе "История дробных
чисел”.
Учитель: Прежде мы вспомним некоторые
определения и ответим на следующие вопросы:
Какие дробные числа появились первыми? И как вы
думаете почему?Какие виды дробей вы знаете?Какие дроби называются неправильными? А какие –
правильными?
Учитель: А у вас не возникал вопрос "Как же
возникли дробные числа”?
Ученики: Возникал.
Учитель: Что же надо сделать, чтобы узнать
историю дробных чисел.
Ученик 1: Надо изучить специальную литературу
об истории дробных чисел.
Ученик 2: Изучить классификацию натуральных
чисел.
Ученик 3: Для этого надо посетить библиотеки,
читальные залы.
Учитель 4: Правильно. Значит, перед нами стоит
цель: "Изучить историю возникновения дробных
чисел”. И следующие задачи:
1. Посетить библиотеку и подобрать материал об
истории дробных чисел.
Ученик 5: Кроме натуральных чисел, есть и
другие числа – дроби. Дроби возникают, когда
натуральное число делят на равные части: надвое,
на три части, на десять частей и т. д. Но мало
знать, что такое дробь. Нужно уметь сравнивать их,
выполнять над дробями действия, решать всякие
задачи с дробями.
Людям часто приходится делить целое на доли.
Самая известная доля – это, конечно, половина.
Слова с приставкой "пол” можно услышать,
пожалуй, каждый день: полчаса, полкилограмма,
полбулки.
Но есть и другие употребительные доли.
Например, четверть, десятая, сотая. Когда
образуются доли? Тогда, когда один предмет
(буханка хлеба, лист бумаги) или единица
измерения (час, килограмм) делятся на равные
части. Доля это каждая из равных частей единицы.
Название доли зависит от того, на сколько равных
частей разделили единицу. Разделили на две части
название доли "половина”, на три – "треть”, на
четыре – "четверть”.
А если на пять, на шесть, семь частей, то
пользуются словами "пятая, шестая,, седьмая” и т.
д. Четверти по-другому называют четвертыми, трети
– третьими, а половины – вторыми долями.
Для записи любой доли используют
горизонтальную черточку. Ее называют дробной
чертой. Над ней ставится единица, а под чертой
пишется число равных частей, на которые единица
делится. Например, вторая, двадцать первая, сто
пятая доля записываются: 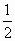 , , 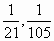 . Читают: "одна вторая”, "одна
двадцать первая”, "одна сто пятая”. Если число
равных частей, на которые поделена единица,
обозначено буквой n, то эту букву и пишут под
дробной чертой: . Читают: "одна вторая”, "одна
двадцать первая”, "одна сто пятая”. Если число
равных частей, на которые поделена единица,
обозначено буквой n, то эту букву и пишут под
дробной чертой: 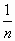 . Читают: "одна энная” . Читают: "одна энная” Зачем нужны доли? Ответить очень просто: при
измерении величин часто бывает невозможно
обойтись только целыми единицами. Представьте,
например, что для измерения длины нам разрешили
пользоваться только целыми метрами. Как тогда мы
бы смогли измерить рост человека? Или спортивные
результаты в прыжках? В таких случаях пользуются
сантиметрами.
А в технике часто нужны более мелкие доли метра
– тысячные. Они, как вы знаете, называются
миллиметрами. И более крупные доли метра бывают
полезны, например десятые. Как из долей
получаются дроби? Возьмем например, число "две
девятых”. Это не натуральное число, но не доля
единицы. Это сумма двух одинаковых долей. Для
чисел, которые являются или долями, или суммами
долей, используют общее название – дробные
числа. Дробные числа называют и просто дробями.
ДРОБЬ – ЭТО ИЛИ ДОЛЯ, ИЛИ СУММА НЕСКОЛЬКИХ
ОДИНАКОВЫХ ДОЛЕЙ.
Так, что число "две девятых” –
это дробь. Цифрами она записывается: 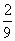 . Дробь . Дробь 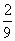 равна сумме
двух одинаковых девятых долей: равна сумме
двух одинаковых девятых долей: 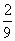 = = 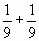 . . Для записи дроби используют дробную черту и два
натуральных числа. Под дробной чертой пишут знаменатель
дроби. Он показывает, из каких долей складывается
дробь. Над чертой пишется числитель дроби. Он
показывает, суммой скольких долей является
дробь.
Ученик 6: Наша нумерация десятичная. Такое
название произошло от правила: единица каждого
разряда в 10 раз больше единицы предыдущего
младшего разряда.
Разряд единицы самый младший в записи
натуральных чисел. единица предшествующего
младшего разряда должна быть в 10 раз меньше
единицы каждого разряда.
Вот люди и договорились правее разряда единиц
помещать разряд десятых долей. А чтобы
указать, где кончаются единицы и начинаются
десятые доли, перед десятыми долями ставят запятую.
Например, запись 34,2 обозначает число 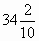 . Число 5 . Число 5 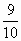 можно записать:
5,9. можно записать:
5,9.
Разряды справа от запятой можно продолжать и
дальше. Что будет обозначать единица второго
такого раз ряда? Чтобы сохранялось правило, она
должна быть в 10 меньше, чем 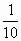 . Значит, это . Значит, это 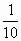 : 10, т.е. : 10, т.е. 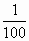 . .
1-й разряд после запятой – десятые доли,
2-й разряд после запятой – сотые доли,
3-й разряд после запятой – тысячные доли.
Дробь, записанную с помощью цифр и запятой,
называют десятичной дробью, дробь, записанную с
помощью дробной черты, называют обыкновенной
дробью.
Как и натуральные числа, всякую десятичную
дробь можно представить в виде суммы разрядных
слагаемых.
Например, 27, 8056 = 20 + 7 + 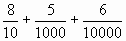 . . В таблице изображены несколько первых разрядов
после запятой и записаны в неё цифры,
обозначающие разрядные слагаемые числа 27, 8056.
Ученик: попробуем записать обыкновенную
дробь 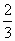 десятичной дробью. Для этого надо числитель
делить на знаменатель. Вычислив, несколько цифр
частного увидим закономерность, с которой эти
цифры появляются. Видно, что будут получаться
одни 6. Но ведь так можно продолжать без конца.
Поэтому получающуюся дробь и называют бесконечной
десятичной дробью. Записать ее полностью
невозможно. Так что где-то придется оборвать
запись и поставить многоточие. Надо только, чтобы
была понятна закономерность, с которой цифры
идут друг за другом. Для дроби
десятичной дробью. Для этого надо числитель
делить на знаменатель. Вычислив, несколько цифр
частного увидим закономерность, с которой эти
цифры появляются. Видно, что будут получаться
одни 6. Но ведь так можно продолжать без конца.
Поэтому получающуюся дробь и называют бесконечной
десятичной дробью. Записать ее полностью
невозможно. Так что где-то придется оборвать
запись и поставить многоточие. Надо только, чтобы
была понятна закономерность, с которой цифры
идут друг за другом. Для дроби 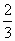 мы обнаружили выше такую
закономерность. мы обнаружили выше такую
закономерность. Можно записать: 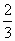 =0,6666... =0,6666...
Бесконечные десятичные дроби – это тоже числа.
Их можно складывать и вычитать, умножать и
делить, сравнивать между собой. Сравнивают их по
тому же правилу, что и конечные (т.е. обычные)
десятичные дроби. Например, 10,63186318... > 10,631846318…,  так как в разряде
стотысячных долей у первого числа стоит цифра 6, а
у второго – 4. так как в разряде
стотысячных долей у первого числа стоит цифра 6, а
у второго – 4. Давайте отбросим в бесконечной десятичной
дроби все цифры, начиная с некоторого разряда. У
нас получится конечная десятичная дробь.
Например, из дроби 0,666666... можно получить конечные
дроби 0,6; 0,66; 0,666; 0,6666 Говорят, что каждая из них – приближение
с недостатком данной бесконечной десятичной
дроби. Из этих приближений можно выстроить
бесконечную цепочку неравенств: 0,6<0,66<0,666<… .
Каждая дробь в цепочке меньше данного числа
0,666666...; и чем больше цифр содержит дробь, тем она б
л и ж е к этому числу.
Теперь снова отбросим в бесконечной десятичной
дроби все цифры, начиная с некоторого разряда, но
последнюю цифру увеличим на единицу. Тогда мы
опять получим конечную десятичную дробь. Она
будет больше данной бесконечной десятичной
дроби. Ее называют приближением с избытком.
Например, для числа 0,666666,.. дроби 0,7; 0,67; 0,667; ... –
приближения с избытком. Каждая из этих дробей
больше числа 0,666666...; и чем больше цифр содержит
дробь, тем она ближе к этому числу.
Чем больше цифр взято в приближении данного
числа, тем ближе получающаяся конечная
десятичная дробь к данному числу.
Помня, что 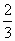 =0,6666... мы можем получить много приближенных
равенств.
=0,6666... мы можем получить много приближенных
равенств.
Валера: Вавилоняне работали только с
шестидесятеричными дробями. Т.к. знаменателями
таких дробей служат числа 60, 602 , 603 и
т.д., то такие дроби, как 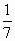 ,
нельзя было точно выразить через
шестидесятеричные: выражали через них
приближенно. Т.к. система счисления у вавилонян
была позиционной, они действовали с
шестидесятеричными дробями с помощью тех же
таблиц, что и для натуральных чисел. ,
нельзя было точно выразить через
шестидесятеричные: выражали через них
приближенно. Т.к. система счисления у вавилонян
была позиционной, они действовали с
шестидесятеричными дробями с помощью тех же
таблиц, что и для натуральных чисел. Шестидесятеричными дробями, унаследованными
от Вавилона, пользовались греческие и арабские
математики и астрономы. Но было неудобно
работать над натуральными числами, записанными
по десятичной системе, и дробями, записанными по
шестидесятеричной. А работать с обыкновенными
дробями было уж совсем трудно. Поэтому
голландский математик Симон Стевин предложил
перейти к десятичным дробям. Сначала их писали
весьма сложно, но постепенно перешли к
современной записи. Сейчас ЭВМ используют
двоичные дроби, которые когда-то применяли и на
Руси: половина, четь, полчети, пол-полчети и т. д.
Интересная система дробей была в Древнем Риме
– двенадцатеричная. Медную монету, а
впоследствии единицу веса – асс римляне
делили на двенадцать равных частей – унций.
Двенадцатую долю асса называли унцией. А путь,
время и другие величины сравнивали с наглядной
вещью – весом. Например, римлянин мог сказать,
что он прошел семь унций пути или прочел пять
унций книги. Имелось в виду, что пройдено 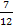 пути или
прочтено пути или
прочтено 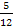 книги. А для дробей, получающихся
сокращением дробей со знаменателем 12 или
раздроблением двенадцатых долей на более мелкие,
были особые названия. Даже сейчас иногда говорят:
"Он скрупулезно изучил этот вопрос”. Это значит,
что вопрос изучен до конца, что ни одной самой
малой неясности не осталось. А происходит
странное слово "скрупулезно” от римского
названия книги. А для дробей, получающихся
сокращением дробей со знаменателем 12 или
раздроблением двенадцатых долей на более мелкие,
были особые названия. Даже сейчас иногда говорят:
"Он скрупулезно изучил этот вопрос”. Это значит,
что вопрос изучен до конца, что ни одной самой
малой неясности не осталось. А происходит
странное слово "скрупулезно” от римского
названия 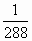  асса – "скрупулус”.
В ходу были и такие названия: "семис” –
половина асса, "секстанс” – шестая его доля,
"семиунция” – полунции, т.е. асса – "скрупулус”.
В ходу были и такие названия: "семис” –
половина асса, "секстанс” – шестая его доля,
"семиунция” – полунции, т.е. 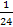 асса, и т.д. Всего
применялось 18 различных названий дробей.
Чтобы работать с дробями, надо было для этих
дробей помнить и таблицу сложения, и таблицу
умножения. Поэтому римские купцы твердо знали,
что при сложении триенса ( асса, и т.д. Всего
применялось 18 различных названий дробей.
Чтобы работать с дробями, надо было для этих
дробей помнить и таблицу сложения, и таблицу
умножения. Поэтому римские купцы твердо знали,
что при сложении триенса ( асса) и секстанса получается
семис, а приумножении беса ( асса) и секстанса получается
семис, а приумножении беса ( асса) на сескунцию ( асса) на сескунцию ( унции, то
есть унции, то
есть  асса) получается унция. Для облегчения работы
составлялись специальные таблицы, некоторые из
которых дошли до нас.
асса) получается унция. Для облегчения работы
составлялись специальные таблицы, некоторые из
которых дошли до нас.
Ученик 7: Из – за того, что в двенадцатеричной
системе нет дробей со знаменателями 10 или 100,
римляне затруднялись делить на 10, 100 и т. д. При
делении 1001 асса на 100 один римский математик
сначала получил 10 ассов, потом раздробил асс на
унции и т. д. Но от остатка он не избавился. Чтобы
не иметь дела с такими вычислениями, римляне
стали использовать проценты. Они брали с
должника лихву (то есть деньги сверх того, что
было дано в долг). При этом говорили: не "лихва
составит 16 сотых суммы долга”, а "на каждые 100
сестерциев долга заплатишь 16 сестерциев лихвы”.
И сказано то же самое, и дробей использовать не
пришлось! Так как слова "на сто” звучали
по-латыни "про центум”, то сотую часть и стали
называть процентом. И хотя теперь дроби, а
особенно десятичные дроби, известны всем,
проценты все-таки применяются и в финансовых
расчетах, и в планировании, то есть в различных
областях человеческой деятельности. А раньше
применяли еще и промилли – так называли
тысячные доли (по-латыни "про милле” – на
тысячу). В отличие от процентов, которые
обозначают знаком %, промилли обозначают ‰.
Ученик 8: В греческих сочинениях по
математике дробей не встречалось. Греческие
ученые считали, что математика должна заниматься
только целыми числами. Возиться с дробями они
предоставляли купцам, ремесленникам, а также
астрономам, землемерам, механикам и другому
"черному люду”. Но старая пословица говорит:
"Гони природу в дверь – она влетит в окно”.
Поэтому и в строго научные сочинения греков
дроби проникали с "заднего хода”. Кроме
арифметики и геометрии, в греческую науку
входила музыка. Музыкой греки называли учение о
гармонии. Это учение опиралось на ту часть нашей
арифметики, в которой говорится об отношениях и
пропорциях. Греки знали: чем длиннее натянутая
струна, тем ниже получается звук, который она
издает, а короткая струна издает высокий звук. Но
у всякого музыкального инструмента не одна, а
несколько струн. Для того чтобы все струны при
игре звучали "согласно”, приятно для слуха,
длины звучащих частей их должны быть в
определенном отношении. Поэтому учение об
отношениях и дробях использовалось в греческой
теории музыки.
Ученик 9: Современную систему записи дробей с
числителем и знаменателем создали в Индии.
Индийцы широко употребляли "обыкновенные”
дроби. Наше обозначение обыкновенных дробей при
помощи числителя и знаменателя было принято в
Индии еще в VIII веке до н.э. однако без дробной
черты. Только там писали знаменатель сверху, а
числитель – снизу.
А записывать дроби в точности, как сейчас, стали
арабы.
Учитель: Что еще надо сделать, чтобы написать
учебно-исследовательскую работу "История
дробных чисел”.
Ученик 10: Записать источники информации,
подготовить приложения (планшет, схемы, фото),
составить словарь терминов.
Учитель: Спасибо. Молодцы. Вы сможете
подготовить реферат по теме "История дробных
чисел”.
|

