«Теория вероятностей есть, в сущности, нечто иное, как здравый смысл, сведённый к исчислению»
Лаплас
Основные цели:
- Дать основное представление о случайности нашей жизни.
Формирование представлений о понятиях: «теория вероятностей», «частота
случайного события».
- Продемонстрировать границы применимости классического определения, неразрывно связанного с равновозможностью исходов
- Воспитывать логическое мышление учащихся.
- Воспитывать уважение к мнению других, умение слушать и рассуждать.
Ход урока
Организационный момент, сообщение темы и целей урока.
Математическая разминка.
Вычислите: а) 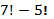 ; б) ; б) 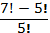 ; в) ; в) 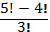 ; г) ; г) 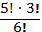
Ознакомление с новым материалом.
Купив лотерейный билет, мы можем выиграть, а можем не выиграть;
завтра на уроке математики вас могут вызвать к доске, а могут и не
вызвать. Все эти события, можно назвать какими? (случайными). Можно
привести и более обыденные примеры. Под потолком висит лампочка — вы не
знаете, когда она перегорит. Будет ли завтра снег, никому наверняка
неизвестно, даже бюро погоды ошибается. Учитель не знает, сколько
ошибок сделает школьник в контрольной работе. (Учащиеся могут привести
свои примеры случайных событий).
В повседневной жизни в разговоре часто используется слово
«вероятность», например: «это невероятный случай», «вероятнее всего он
опоздает» и т.д. Здесь интуитивно оценивается возможность того или иного
события, исходя из здравого смысла, интуиции. Например, мы заранее
знаем, что на детский сеанс пойдет большинство школьников, чем
взрослых, или что при выполнении многих видов работ вредна
торопливость, так как в спешке можно сделать ошибки.
Однако в жизни чаще встречаются события, сравнить и оценить которые,
основываясь только на интуиции, невозможно и трудно. Например, это
можно сказать про события «герб появится 2 раза при пятикратном
бросании монеты». Каждое событие обладает определенной степенью
возможности наступления, то есть определенной оценкой. Такую оценку
называют вероятностью события.
Определение: Мы назовём событие случайным, если нельзя утверждать,
что это событие в данных обстоятельствах непременно произойдёт.
В теории вероятности шанс того, что случайное событие произойдёт,
выражают числом. Это число называют вероятностью случайного события.
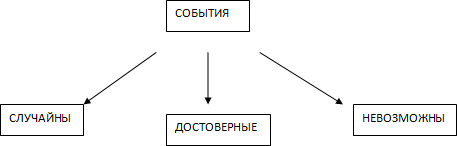
Если событие никогда не наступает(его шансы равны нулю), то вероятность
этого события полагают равной 0.Такое событие называют невозможным.
Если же событие наступает всегда, его вероятность полагают равной 1.
Такое событие называют достоверным. Вероятность остальных- это значения
между 0 и 1.
Обозначим какое – либо случайное событие большой латинской буквой A.
Вероятность события обозначается большой латинской буквой P. Первой
буквой французского слова probabilite, что в переводе означает –
возможность, вероятность. Тогда вероятность события А будем обозначать:
Р(А) = m/n , где m–число благоприятных исходов, а n – число всех
возможных исходов.
Определение: Вероятностью события А равна
отношению числа m исходов испытания, благоприятствующих наступлению
события А, к общему числу n всех равновозможных несовместимых исходов,
т.е. 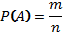 . .
Следовательно, для нахождения вероятности события необходимо:
- подсчитать все возможные несовместимые исходы n,
- выбрать число интересующих нас исходов m
- вычислить отношение m и n.
Монетка в теории вероятности.
 
Математическая монета, используемая в теории вероятности имеет
только две стороны, одна из которых называется «орёл», а другая «
решка». Монету бросают, и она падает одной из сторон вверх.
Математическая монета считается симметричной. Это означает, что
брошенная на стол монета имеет равные шансы выпасть «орлом» или
«решкой».
Практическое задание: Проведём опыт с бросанием 15 монет по 50 раз
| № эксперимента по 50 опытов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| Число выпадений «орла» |
23 |
26 |
25 |
24 |
23 |
26 |
27 |
25 |
24 |
25 |
26 |
23 |
25 |
24 |
28 |
| Число выпадений «решки» |
27 |
24 |
25 |
26 |
27 |
24 |
23 |
25 |
26 |
25 |
24 |
27 |
25 |
26 |
22 |
Найдем вероятность появления «орла» (учащиеся считают и сообщают
свои результаты). Нетрудно заметить, что результат у многих из вас
похож и примерно равен числу 0,5. Тот факт, что вероятность появления
«орла» равна 0,5, не означает, что в любой серии экспериментов (это
было и в ваших опытах) «орёл» появится ровно в половине случаев. Но если
число экспериментов достаточно велико, то можно дать прогноз, что
«орёл» выпадет примерно в половине случаев. То есть, если монета
однородна и имеет правильную геометрическую форму, то шансы выпадения
орла и решки одинаковы.
Зарождение теории вероятностей произошло в поисках ответа на вопрос:
как часто наступает то или иное событие в большой серии испытаний со
случайными исходами, которые происходят в одинаковых условиях?
Игральные кости в теории вероятности

Игральный кубик или игральная кость тоже служит прекрасным средством
для получения случайных событий. Правильные (симметричные) кости
обеспечивают одинаковые шансы выпадения каждой грани. Все
равновозможные исходы однократного бросания пары костей можно записать в
виде
(1;1) (1;2) (1;3) (1;4) (1;5) (1;6)
(2;1) (2;2) (2;3) (2;4) (2;5) (2;6)
(3;1) (3;2) (3;3) (3;4) (3;5) (3;6)
(4;1) (4;2) (4;3) (4;4) (4;5) (4;6)
(5;1) (5;2) (5;3) (5;4) (5;5) (5;6)
(6;1) (6;2) (6;3) (6;4) (6;5) (6;6)
(здесь пара (а;в) означает что на первой кости выпало а очков, а на второй в)
Практическое задание: Проведите опыты по выбрасыванию пары костей 10 раз и на найдите частоту выпадения 7 очков
Первичное закрепление изученного.
Рассмотрим такие примеры:
1. Бросают игральный кубик, то есть небольшой куб,
на гранях которого нанесены очки 1, 2, 3, 4, 5, 6. При бросании
игрального кубика на его верхней грани может выпасть одно очко, два
очка, три очка и т. д. Каждый из этих исходов является случайным.
Какова на ваш взгляд вероятность выпадения 4 очков? (Р(А) = m/n, Р(А) =
1/6).
2. Какова вероятность появления четных очков при одном бросании игрального кубика?
Решение: Пусть А – событие «выпадет четное число» n =6, так как
число возможных исходов 6 (1; 2; 3; 4; 5; 6); n =3, так как только 3
четных очка (2; 4; 6;). Значит Р(А) = 3:6 = 0,5.
3. Из карточек составили слово «статистика». Какую карточку с буквой вероятнее всего вытащить? Какие события равновероятные?
Решение: Всего в слове статистика 10 букв. Буква «с» встречается 2
раза – P(с) = 2/10 = 1/5; буква «т» встречается 3 раза – P(т) = 3/10;
буква «а» встречается 2 раза – P(а) = 2/10 = 1/5; буква «и» встречается 2
раза – P(и) = 2/10 = 1/5; буква «к» встречается 1 раз – P(к) = 1/10.
Вероятнее всего вытащить карточку с буквой «т». Вероятность одинакова у
букв «с», «а», «и»: P(с) = Р(а) = Р(и) = 2/10 = 1/5.
4. В классе 30 учащихся. Из них 12 мальчиков,
остальные девочки. Известно, что к доске должны быть вызваны трое
учащихся. Какова вероятность, что это девушки?
Решение: Число всех возможных исходов равно количеству способов,
которыми можно выбрать троих учащихся из 30, то есть n = C330. Число
благоприятных исходов равно количеству способов, которыми можно выбрать
троих учащихся из числа девочек, то есть m = C318. Тогда Р(А) = m/n =
204/1015, где Скn = n!/k!(n – k)!.
Проблемная задача.
Найти вероятность следующих событий и сделать выводы:
- Какова вероятность того, что после зимы будет осень?
- Какова вероятность того, что после ночи наступит утро?
- Какова вероятность того, что вас вызовут к доске, если в классе 25 человек?
Обобщение и систематизация полученных знаний.
- Как называется наука, изучающая случайные события? Приведите примеры случайных событий
- По какой формуле можно вычислить вероятность случайного события?
- Какие события называют равновероятными?
- Какие события называют достоверными, и какие невозможными? Чему равны их вероятности?
- Приведите примеры невозможных и достоверных событий?
Классическая теория вероятностей рассматривает вероятность как
отношение числа благоприятных событий ко всем возможным событиям. При
этом предполагается, что все рассмотренные случаи являются
равновозможными, равновероятными. Для того чтобы найти вероятность
некоторого события, надо правильно определить число равновозможных
исходов испытания и число благоприятных для этого исходов.
Теория вероятностей неразрывно связана с нашей повседневной жизнью. Этот раздел изучения великой математики подготовит нас к:
- выбору наилучшего из возможных вариантов;
- оценке степени риска;
- шансу на успех; и т. д.
Выставление оценок.
Задание на дом:
- Из карточек составили слово «математика». Какую карточку с буквой вероятнее всего вытащить? Какие события равновероятные?
- В ящике 15 деталей, среди которых 10 окрашенных. Сборщик наугад извлекает 3 детали. Найти вероятность того, что они окрашены.
- В классе 25 учеников, 8 из них – отличники. По списку наугад
отобрали 9 человек для участия в конкурсе. Найти вероятность того, что
среди них – 5 отличников.
Резервные задания.
На случай досрочного выполнения всем классом рассмотренных заданий и
обеспечения занятости и развития, учащихся планируется использовать
дополнительные задания:
- Бросаются 2 игральных кубика. Какова вероятность того, что сумма выпавших очков меньше13?
- При перевозке ящика, в котором содержались 21 стандартная и 10
нестандартных деталей, утеряна одна деталь, причем неизвестно какая.
Наудачу извлеченная (после перевозки) из ящика деталь оказалась
стандартной. Найти вероятность того, что была утеряна: а) стандартная
деталь, б) нестандартная деталь.
- Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что это число кратно 5?
- Из колоды в 36 карт наудачу извлекаются 3 карты. Определите
вероятность того, что сумма очков в этих картах равна 21, если валет
составляет 2 очка, дама – 3, король – 4, туз – 11, а остальные карты –
соответственно 6, 7, 8, 9, 10 очков.
| 
