Цели:
- познакомить учащихся с решением уравнений с
модулями как аналитическим способом, основанном
на определении модуля, так и геометрическим
методом решения;
- развивать самостоятельность, используя для
этого проблемные ситуации;
- воспитывать организованность.
I. Организационный момент
II. Устные упражнения
По ходу выполнения устных упражнений
необходимо вспомнить:
- определение модуля, изученного в 6 классе;
- обозначение модуля;
- геометрический смысл абсолютной величины
действительного числа;
- расстояние между двумя точками.
Запишем основные понятия, определения и
свойства модуля.
1. Определение
Модулем действительного числа называется
само это число, если оно не отрицательное, и
противоположное ему число, если данное число
отрицательное.
Обозначение модуля: || (прямые скобки).
Из определения модуля следует:
1.1. 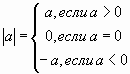
1.2. Модуль есть число неотрицательное (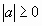 ). ).
1.3. 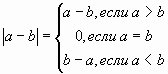
1.4. Модули противоположных чисел равны (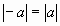 ),
действительно: ),
действительно:
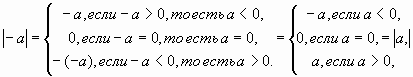
откуда 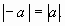
2. Геометрический смысл модуля
2.1. Известно, что между множеством
действительных чисел и множеством точек
числовой прямой существует взаимооднозначное
соответствие. Это дает возможность
рассматривать точки числовой прямой как модели
действительных чисел, иными словами,
отождествлять точки числовой прямой с
действительными числами, которые будем называть
в дальнейшем просто "точками”.
Учитывая, что положение точки на числовой
прямой определяется расстоянием ее от начала
отсчета и направлением, и учитывая 1.4,
естественно отождествлять понятие "модуля” с
расстоянием точки до начала отсчета.
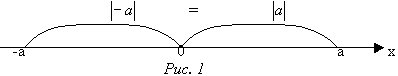
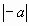 –
расстояние точки –а до начала отсчета 0, –
расстояние точки –а до начала отсчета 0,
 –
расстояние точки а до начала отсчета 0. –
расстояние точки а до начала отсчета 0.
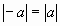
2.2. Расстояние между двумя точками. Здесь
возможны три случая:
Обозначим r(а; b) – расстояние между точками а и b.
а)
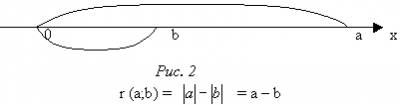
б)
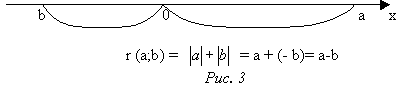
в)
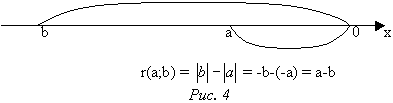
Таким образом расстояние между двумя точками
числовой прямой то есть длина любого отрезка числовой прямой
равна модулю разности его концов.
Примеры:
1) 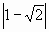 можно
рассматривать как r(1;2) можно
рассматривать как r(1;2)
2) 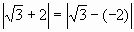 можно
рассматривать как r(3;-2) можно
рассматривать как r(3;-2)
3) 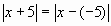 = r(х;-5) = r(х;-5)
Устные упражнения:
Найдите модуль каждого из чисел: 81; 1,2; -3,6; 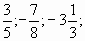 -74; 0. -74; 0.
Найдите расстояние (в единичных отрезках) от
начала отсчета до каждой из точек:
А(2,3); В(-4,2); С(312,7); Д(-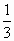 );Е(0). );Е(0).
Найдите значение выражения: 4. Точка А лежит от начала отсчета влево на 5,8
единицы, а точка В – вправо на 9,8 единицы. Чему
равна координата каждой точки? Чему равен модуль
каждой координаты?
Известно, что  =7. Чему равен =7. Чему равен 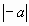 ? ?
Из двух чисел выберите то, у которого модуль
больше?
а) -700,1 и 0,24
б) -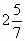 и 3 и 3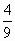
в) -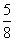 и - и -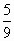
7. Найти расстояние между двумя точками:
а) -5,2 и 3,1
б) 8 и -2,6.
8. Решить уравнение: По ходу выполнения устных упражнений по
учебному пособию Е.В. Смыкаловой учащиеся, с
помощью учителя, изучают основные свойства
модуля.
III. Теоретическая часть урока
Рассмотрим решение уравнений, содержащих знак
модуля аналитическим и геометрическим
способами.
1) Решить уравнение: 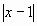 = 4 = 4
Решение:
I cпособ (аналитический).
Уравнение равносильно совокупности двух
уравнений: Ответ: 5; -3.
II cпособ (геометрический): существуют две
точки х, удаленные от точки 1 на расстояние,
равное 4.

следовательно, Ответ: 5; -3.
IV. Практическая часть урока
Решить уравнение: 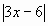 =9 =9
Решение:
I cпособ (аналитический).
Уравнение равносильно совокупности двух
уравнений: Ответ: 5; -1.
II cпособ (геометрический):
а) обозначим 3х=у, тогда 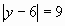
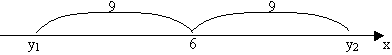

Ответ: 5; -1.
Решить уравнение: 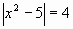
Решение:
I cпособ (аналитический).
Уравнение равносильно совокупности двух
уравнений: Ответ: -3; -1; 1; 3.
II cпособ (геометрический):
Как и в задаче №2 можно решить способом
подстановки (х2=у), но можно решить данное
уравнение как линейное, относительно х2.
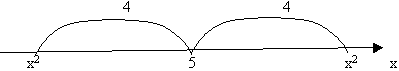
Ответ: -3; -1; 1; 3.
| 
