|
1) Изучить формулу сложных процентов,
сравнить графики простых и сложных процентов,
способствовать формированию навыков решения
практических задач по теме урока.
2) Развивать логическое мышление,
память учащихся, творческие и аналитические
способности учащихся.
3) Воспитывать активную жизненную
позицию, интерес к знаниям, способствовать
профессиональному самоопределению учащихся.
- Раздаточный материал с таблицей "Коэффициенты
наращения сложных процентов”,
- Печатные формулы простых и сложных процентов.
- Заготовка для графика.
Ход урока
I. Организационный момент
II. Защита домашнего задания
1) Обязательная задача (текст
заготовлен на доске)
Предприятие располагает собственным
капиталом в 100 млн. руб. и берет в банке взаймы под
10% годовых еще 50 млн. руб. Норма прибыли
предприятия (рентабельность производства)
составляет 30%. Чему равен доход предприятия за
год работы?
Решение:
- 100 + 50 = 150 (млн. руб.)
- 150 · 0,3 = 45 (млн. руб.) – полученная прибыль на 150
млн. руб.
- 50 · 0,1 = 5 (млн. руб.) – выплата за ссуду,
- 45 – 5 = 40 (млн. руб.) – прибыль предприятия.
Ответ: 40 млн. руб.
2) Творческое задание: задачи,
составленные учащимися с использованием
различных источников информации.
2.1. По итогам деятельности разреза
"Нерюнгринский” за 2003 г.:
| |
План |
Выполнение |
| Вскрыша |
46 млн.т. |
47млн454тыс.м? |
| Добыча |
8млн.т. |
8 млн. 302тыс.178т. |
| Коксующийся уголь |
5 млн.т. |
5 млн. 202 тыс.163 т. |
Определить на сколько % п6еревыполнен
план.
2.2. По образованию (По материалам
газеты "Час досуга”)
В анализе работы Нерюнгринского
района за 2003 год, говорится о том, что на 1. 09. 2003
года в школах района 10,5% педагогов имели высшую
категорию и 32.5% имели I категорию. А сейчас
давайте вычислим, сколько педагогов высшей и
первой категории работает в нашей школе (в
процентах от общего количества).
Всего в СОШ №18 – 65 педагогов.
Высшую категорию имеют 7 педагогов;
р=7:65 100=10,7%.
I категорию – 15 педагогов; р=15:65 100=23,1%
Получается, что в нашей школе
преподавателей высшей категории примерно
столько же сколько в среднем по району, а
учителей I категории меньше, чем в районе. Вот
такой у нас педагогический коллектив.
2.3. Работа администрации города с
письмами граждан
В газете "Индустрия севера” за 16
января 2004 года помещен материал о
пресс-конференции главы муниципального
образования "Нерюнгринский район” В. В.
Старцева с представителями городских и
республиканских СМИ, в котором меня
заинтересовали некоторые факты.
Цитирую.
"За минувший год к главе
администрации поступило 681 письменное обращение.
Все они рассмотрены, 50% решены положительно, в 175
случаях отказано, по 138 дано разъяснение. По
поводу зарплаты в 2002 году к главе обращались 32
раза, а в 2003–21раз.”
Выясним, на сколько процентов число
обращений к главе администрации по поводу
зарплаты в 2002 году больше, чем в 2003?
32 – число обращений в 2002году (В)
21 – число обращений в 2003 году (А)
Найти на сколько процентов В больше А.
Решение:
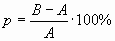 ; ; 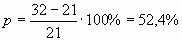
Ответ: В2002 году к главе администрации
поступило на 52,4% обращений больше, чем в 2003 году.
III. Изучение нового материала:
10 Вводная беседа учителя.
Почему в 2003 году писем по поводу
заработной платы в администрацию города
поступило на 53% меньше чем в 2002 году?
- Учащиеся выдвигают предположения.
Каждое высказанное предположение
может быть верным, а может быть и ложным. Для того
чтобы узнать истинную причину нам, видимо, на
данный момент недостаточно информации. Для того
чтобы полностью владеть ситуацией, необходимо
быть хорошо информированным по существу вопроса.
На предыдущих занятиях мы с вами
рассматривали задачи на проценты, задачи на
простые проценты, но этим не исчерпывается
применение процентов в экономике, и сегодня мы
расширяем свои знания в этой области.
Тема занятия "Сложные проценты”
2) Изложение темы:
Пусть банк выплачивает по
сберегательному счету простые проценты по
ставке I в год, причем эта ставка остается
неизменной в течение двух лет. Вкладчик может
поступить по разному:
I. Если он закроет счет через год, то он
получит сумму S (1) = S (0) · (1 +I)
Допустим, что он положит эту сумму еще
на один год с теми же условиями, тогда через
второй год он получит: S (2) = S (1) · (1 + I) = S (0) · (1+I) 2
II. Если он не переоформит свой вклад, то
по простым процентам он получит за два года:
S (2) = S (0) · (1 + 2I)
Равны ли эти суммы? Сравним их:
S (0 ·1 + I) 2– S(0) · (1 + 2I) = S(0) · (1 + 2I +I
–1 – 2I ) = S(0) · I
Так какой же способ выгоднее для
вкладчика?
- I. Так как вкладчик получает при этом
на S (0) · I больше.
Величина S(0)·I – приращение на
проценты, полученные за первый год или, так
называемые "проценты на проценты”.
Чтобы предотвратить частое
переоформление вкладов и для поощрения
долгосрочных вкладов, в коммерческой практике
принято выплачивать сложные проценты.
Исходная сумма или база (S (0)) для
начисления сложных процентов увеличивается с
каждым периодом начисления, а для простых
процентов база постоянна (S (0)).
Запишем в словари ОПРЕДЕЛЕНИЕ.
Капитализацией процентов
называется присоединение начисленных процентов
к сумме, являющейся базой для их начисления.
Выведем формулу расчета наращенной
суммы S (n) с годовой процентной ставкой I при
условии, что проценты начисляются и
капитализируются один раз в год.
– К доске вызывается ученик вывод
формулы:
S (1) = S (0) +S (0) ·I =S (0) · (1 + I)
S (2) = S (1) + S (1) · I = S (1) · (1 + I) = S (0) · (1 + I)2
S (3) = S (0) · (1 + I)3·
……………………….. ·
S (n) = S(0) · (1 + I) n – Формула
сложных процентов, где
S (n) – наращенная сумма через n лет
S (0) – базовая сумма
I – процентная ставка по сложным
процентам
N – число периодов наращения
Эта формула описывается
геометрической прогрессией со знаменателем q =
1 + I.
Пример 1. Вы положили в банк 10 тыс.
руб. на срочныи вклад при сложной процентной
ставке 10% годовых. Сколько денег вы получите
через два года?
Дано: S (0) = 10000 руб. , I = 0,1, n = 2.
Найти: S (2).
Решение: S (2) = S(0) · (1 + I)2
S (2) = 10000 · (1 +0,1)2 = 10000 ?
1,21 =12100 руб.
Ответ: 12100 руб.
Отношение 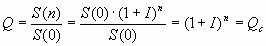
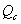 – коэффициент наращения по сложным
процентам – коэффициент наращения по сложным
процентам
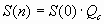
Для начисления сложных процентов в
банках используют "Таблицы коэффициентов
наращения по сложным процентам”, рассмотрим их
(таблицы на столах у всех учащихся )
Устная работа с таблицей:
Назовите коэффициент наращения по
ставке 15% годовых для n = 4 (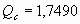 ) )
8% годовых для n =5 (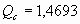 ) )
Пример 2. (Письменно)
Вкладчик открыл счет в сбербанке на
сумму 15000 руб. с годовой процентной ставкой 8.
Какую сумму он будет иметь на счету через 3 года,
через 5 лет?
Решение:
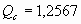 , ,- 15000 ·1,2597 = 18895,5 руб
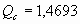 ; 15000
· 1,4693 = 22039,5 руб. ; 15000
· 1,4693 = 22039,5 руб.
IV. Самостоятельная работа с
последующей самопроверкой.
Заполните таблицу:
Вариант |
S (0) тыс. руб. |
n |
I % |
S (n) тыс. руб. |
1 |
500 |
3 |
18 |
821516 |
2 |
400 |
6 |
14 |
877989 |
3 |
50 |
5 |
14 |
96270,73 |
4 |
300 |
6 |
12 |
592146,75 |
Столбец S (n) закрыт до самопроверки.
V. Работа в парах.
Сравните коэффициенты наращения по
простым процентам и сложным при I = 18% годовых.
Заполните таблицу и постройте график
зависимости Q от n.
Q n |
0,25 |
0,5 |
1 |
5 |
10 |
Q = 1 +I·n |
|
|
|
|
|
Qc = (1 +I)n |
|
|
|
|
|
График зависимости Q от n
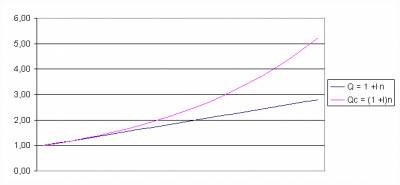
Какой совет вкладчикам банка вы можете
дать, проанализировав расположение графиков?
(Наращение по сложным процентам
выгоднее для вкладчиков).
VI. Пример из классической литературы:
Михаил Евграфович Салтыков – Щедрин
описывает в "Господах Голавлевых” такую сцену:
"...Порфирий Владимирович сидит у себя в
кабинете, исписывая цифирными выкладками листы
бумаги. На этот раз его занимает вопрос: сколько
было бы у него теперь денег, если бы маменька
подаренные ему при рождении дедушкой "на зубок”
100 рублей не присвоила себе, а положила в ломбард
на имя малолетнего Порфирия? Выходит, однако,
немного: всего 800 рублей…”
Задание: Попробуйте по приведенным
цифрам вычислить процентную ставку, которую
платил ломбард в то время по вкладам. Возраст
Порфирия в момент расчетов примем равным
пятидесяти годам.
Решение:
Пусть ставка равна X%,
Тогда S(50) =100·(1 + X)
800 =100 ·(1 +X)n
………………………
X~ 3.9
Итак, в то время ломбард платил 3,9%
годовых.
VII. Домашнее задание:
- Что выгоднее: заплатить за учебу в ВУЗе 10000
условных денежных единиц в начале обучения или
15000 у. д.е. по окончании учебы (через 5 лет).
Процентная ставка равна 10% годовых. - Практическое задание.
Посетите операционный зал сбербанка и
выпишите:
- Виды вкладов,
- Годовые процентные ставки по ним,
- Срок наращения,
- Минимальный взнос.
Составьте задачу и решите ее.
VII. Итоги занятия.
| 
