Цель: организация продуктивной деятельности
школьников, направленной на достижение ими
результатов
Виды деятельности:
- Личностно-ориентированные: Заинтересовать
ученика, обеспечить более широкое представление
об изучаемых предметах (метод индукции);
стимулировать способность иметь собственное
мнение.
- Метапредметные: Умение вступать в речевое
общение, создание письменных высказываний,
адекватно передающих прослушанную и прочитанную
информацию. Владение навыками контроля и оценки
своей деятельности. Сравнивать и
классифицировать объекты по одному или
нескольким предложенным критериям; моделировать
ситуацию, на языке алгебры.Творческое решение
учебных и практических задач.
- Предметные: Использовать понятие
"последовательность” и способы задания
последовательности, строить последовательность
по заданному рекуррентно или в виде общего члена
правилу; решать задачи с применение формул n-го
члена и суммы n первых членов.
Ход урока
1. Проверка домашнего задания (15 минут).
У доски готовятся представить свои способы
решения несколько обучающихся.
Домашняя работа: Решите задачу разными
способами: При встрече 8 человек обменялись
рукопожатиями. Сколько было рукопожатий?
1 способ. Графический
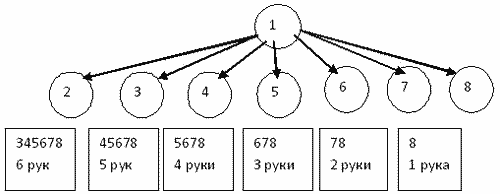
Рисунок 1
Всего рукопожатий = 7+6+5+4+3+2+1=28.
Как вы думаете, как можно назвать 7654321
(последовательностью натуральных чисел)?
По какому правилу задана данная
последовательность? (каждое следующее число
меньше предыдущего на 1, числа убывают, находятся
в числовом промежутке [1;7]... ).
2 способ. Комбинаторика.
Каждому человеку присвоим номер от 1 до 8 и будем
обозначать рукопожатия следующим образом:
Например, 15 - первый пожал руку пятому.
Получим ряд чисел:
12,13,14, 15, 16, 17, 18,
23,24, 25, 26, 27, 28
34, 35, 36, 37, 38
45, 46, 47, 48
56, 57, 58
67, 68
78
Всего комбинаций 28.
Чем отличается каждый ряд от предыдущего, в чем
сходство? (разные числа, разное количество этих
чисел, в каждом столбце второе число одинаковое)
3 способ. (Вычисление с использованием
метода математической индукции).
Используя утверждение 1+2+3+...+n = 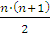 (доказывается
методом математической индукции при n=1.
Равенство выполняется. Предположим, что
равенство справедливо, т.е. 1+2+3+...+n = (доказывается
методом математической индукции при n=1.
Равенство выполняется. Предположим, что
равенство справедливо, т.е. 1+2+3+...+n = 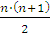 верно. Докажем, что
равенство выполняется и при n+1. верно. Докажем, что
равенство выполняется и при n+1.
1+2+3+...+n+(n+1)=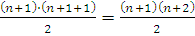
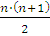 +(n+1)=(n+1)(0,5n+1)= +(n+1)=(n+1)(0,5n+1)=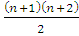 , то есть
выполняется и это утверждение). , то есть
выполняется и это утверждение).
В нашей задаче n=8, следовательно, 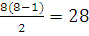 . Используя этот
способ, нашли сумму всех членов
последовательности. . Используя этот
способ, нашли сумму всех членов
последовательности.
Какими понятиями оперировали при решении
задачи? (натуральные числа, последовательность,
убывание/ возрастание, сумма всех членов
последовательности.)
Какие способы моделирования ситуации были
предложены? (графический, табличный,
аналитический).
Какие методы решения предложены? (метод
индукции, просто вычислили подсчетом, используя
формулу подсчета суммы членов арифметической
последовательности).
2. Целеполагание.
Как вы думаете, что мы будем изучать на уроке?
(последовательность чисел, способы задания таких
последовательностей их виды, нахождение суммы
членов арифметической прогрессии, применение
формул для нахождения неизвестных членов
арифметической прогрессии)
3. Творческое задание (5 минут).
Работа в четверках. Определите
закономерность в представленных объектах на
рисунке 1, составьте арифметические прогрессии.
Объясните почему вы так составили. Дорисуйте на
картинке объекты для своей придуманной
арифметической прогрессии.

Рисунок 2
(Возможны разные варианты: по количеству окон,
животных, облаков...)
4. Практическая работа (10 минут).
Вычислите сколько у Миши денег на питание, если
у Вали 1000 рублей, у Пети 960 рублей. Если известно,
что по количеству денег, можно составить
арифметическую прогрессию? Посчитайте сколько
денег у Миши, Вали, Пети вместе? (Представьте свою
версию решения задачи)
- Над задачей можно работать в группах и
защищать свои версии у доски. (или оформленные на
листа А3);
- Самостоятельно (учитель выбирает, разные
варианты и просит рассказать решения);
- Представить как можно больше вариантов
решения каждому ученику.
Например,
1 Вариант
| Миша |
Валя |
Петя |
| ? |
1000 |
960 |
Убывающая прогрессия, в которой разность
прогрессии d=-40, тогда у Миши 1040 рублей. Всего = 3000
рублей.
2 вариант
| Валя |
Миша |
Петя |
| 1000 |
? |
960 |
Убывающая прогрессия, в которой разность
прогрессии d=-20, тогда у Миши будет 980 рублей. Всего
= 2940 рублей.
3 вариант
| Валя |
Петя |
Миша |
| 1000 |
960 |
? |
Убывающая прогрессия, в которой разность
прогрессии d=-40, тогда у Миши будет 920 рублей. Всего
= 2880 рублей.
Можно составлять и возрастающие прогрессии.
5. Дополнительные задания: (10 минут).
Работа с карточками. (Ершова А.П.
Самостоятельные и контрольные работы по алгебре
и геометрии для 9 класса) Учащиеся сами выбирают
уровень сложности.
| Уровень А (оценивается на 3 в случае
решения 50% -100% заданий) |
Уровень В (оценивается на 4 в случае
решения 60%-100%) |
Дополнительное задание (Для учащихся,
которые решили задание уровня В и это задание) |
| Дана арифметическая прогрессия 27, 24...
А) составьте формулу n-го члена прогрессии;
Б) найдите 21 член прогрессии. |
Дана арифметическая прогрессия 29, 24...
Определите входит ли в данную прогрессию число
-41. |
Арифметическая прогрессия задана
формулой 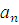 =98-5n. =98-5n. Найдите сумму положительных
членов данной прогрессии. |
Дана арифметическая прогрессия 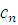 ,в которой ,в которой 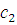 =18; =18; 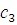 =14. =14. А)
Найдите первый член и разность арифметической
прогрессии.
Б) Найдите сумму первых 8 членов прогрессии. |
Между числами 1 и 4 вставьте 8 чисел так,
чтобы они составляли арифметическую прогрессию.
Найдите сумму членов полученной арифметической
прогрессии. |
|
Рефлексия (3 минуты).
Вопрос группам. (Индивидуальная работа).
Проанализируйте решенные задачи и составьте
план, что вы использовали для решения задач сами,
что узнали нового из решения одноклассников.
Какие приемы можно использовать в дальнейшем.
Домашняя работа (2 минуты).
Придумайте задачу, в которой должно
выполняться два условия (1. Моделирование
реальной ситуации, 2. Используя числа 2,4,6,8,10).
|

