Тип занятия: практическая работа.
Учебно-воспитательные задачи:
- Научить учащихся применять различные методы
решения неравенств с параметром;
- Продолжать формировать умения и навыки
применения решения неравенств;
- Продолжать формировать интерес к математике
посредством решения задач;
- Воспитывать осознанное отношение к процессу
обучения, прививать чувство ответственности за
качество знаний, осуществлять самоконтроль за
процессом решения и оформления упражнений;
- Напоминать, что только осознанное применение
алгоритмов решения неравенств позволит учащимся
качественно усвоить изучаемую тему.
Обеспечение занятия:
- Таблица основных методов решения неравенств с
параметрами;
- Карточки-задания для проверочной работы.
Студент должен знать:
- Алгоритмы решения неравенств с параметром.
Студент должен уметь:
- Применять полученные знания к решению
неравенств с параметром.
Ход занятия
I. Организационный момент.
Задача с параметром.
Нужно усвоить главное:
- Параметр, будучи фиксированным, но неизвестным
числом, имеет двойственную природу.
Во-первых предполагаемая известность
позволяет "общаться” с параметром как с числом.
Во-вторых – степень свободы общения
ограничивается его неизвестностью.
Существует класс задач, где за счет параметра
на переменную накладываются какие – либо
искусственные ограничения. Найти множество всех а, при которых
неравенство х-2 <0 выполняется при всех х Є [1; 2]
III. Повторение опорных знаний учащихся.
Для того чтобы решить задачу, рассмотрим устные
упражнения:
1) Что значит решить задачу с параметром?
Ответ: Значит найти все значения
неизвестного при всех допустимых значениях
параметра
2) Какие методы решения можно использовать?
Ответ: Аналитический метод, метод
интервалов, графический метод.
3) Алгоритмы решений:
- Аналитический метод:
- Рассмотреть совокупность систем.
- Найти решение совокупности систем.
- Работа с параметром.
- Ответ.
- Метод интервалов:
- Рассмотреть функцию (x) и найти область
определения.
- Найти нули функции.
- Отметить положение нулей на числовой оси с
учетом D(f).
- Найти знаки функции в промежутках между её
нулями, начиная с крайнего правого промежутка
(всегда положительна?).
- Работа с параметром.
- Ответ.
- Графический метод:
- Рассмотреть плоскость (х; а).
- Указать точки, где числитель и знаменатель
равны нулю.
- Определить знак неравенства в каждой из четырёх
областей.
- Работа с параметром.
- Ответ.
4) При каких а система 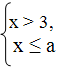 , не имеет решений? , не имеет решений?
Ответ: при а < 3$
5) При каких а система имеет единственное решение?
Ответ: при а = -2 IMAGE11$
6) При каких а существует ровно три целых
числа, являющихся решением системы неравенств 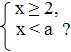
Ответ: при 4<a<5
IV. Решение задачи.
Работа по группам:
1 группа. Аналитический метод решения
неравенства.
Данное неравенство равносильно совокупности
систем:
Итак: а<х<2а+1 , 2а+1<x<а
Рассмотрим три случая:
1) a<x<2a+1,
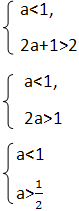
1/2<a<1
2) 2a+1<x<a,
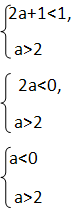
Нет решений
3) 2a+1=a,
a=-1
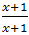 <0 <0
Нет решений
Следовательно, ответ: 1/2<a<1.
2 группа. Графический метод решения
неравенства.
Решим это неравенство методом, аналогичным
методу интервалов.
Для этого на плоскости (х; а) укажем точки, где
х-2а-1=0 и х-а=0 .
Определим знак неравенства в каждой из 4-х
областей. Найдя его в одной точке, например (10;0).
Тогда при переходе через любую прямую меняя знак
дроби.
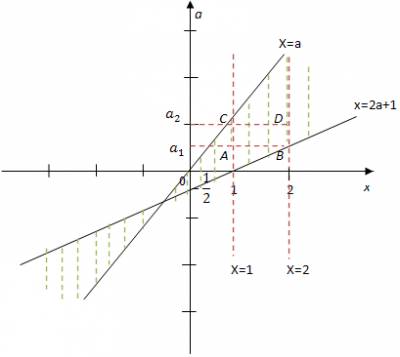
Множество точек плоскости, удовлетворяющих
данному неравенству, расположены в
заштрихованных областях.
Если проведем любую прямую а=a0, то ее
часть, лежащая в заштрихованной области, дает
интервал, в котором содержится х и при а=a0.
V. Применение знаний при решении типовых
примеров.
Решить задачу самостоятельно:
При каких значениях параметра а
неравенство
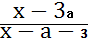 <0
выполняется для всех х из отрезка [1; 3] <0
выполняется для всех х из отрезка [1; 3]
Ответ: 0<a<1/3
VI. Подведение итогов занятия.
| 
