На уроке учащиеся продемонстрировали знания и умения программы: – распознавать виды функции, строить их графики; – отрабатывали навыки построения квадратичной функции; – отрабатывали графические способы решения квадратных уравнений, используя метод выделения полного квадрата.
Мне захотелось уделить особое внимание решению задач с параметром, так как ЕГЭ по математике предлагает очень много заданий такого типа. Возможность применить на уроке такой вид работы дали мне сами ученики, так как они имеют достаточную базу знаний, которые можно углубить и расширить. Заранее подготовленные учащимися шаблоны позволили экономить время урока. В ходе урока мне удалось реализовать поставленные задачи в начале урока и получить ожидаемый результат. Использование физкультминутки помогло избежать переутомления учащихся, сохранить продуктивную мотивацию получения знаний. В целом результатом урока я довольна, но думаю, что есть еще резервные возможности: современные инновационные технологические средства, которыми мы, к сожалению, не имеем возможности пользоваться. Тип урока: закрепление изученного материала. Цели урока: ХОД УРОКА I. Организационный момент – Сегодня на уроке мы обобщим и закрепим графическое решение квадратных уравнений различными способами. В дальнейшем эти навыки нам будут нужны в старших классах на уроках математики при решении тригонометрических и логарифмических уравнений, нахождения площади криволинейной трапеции, а также на уроках физики. II. Проверка домашней работы Разберем на доске № 23.5(г). Решить это уравнение с помощью параболы и прямой. Решение: х2 + х – 6 = 0 Преобразуем уравнение: х2 = 6 – х Введем функции: у = х2; квадратичная функция у = 6 – х линейная, графиком явл. парабола, графиком явл. прямая, Строем в одной системе координат графики функций (по шаблону) 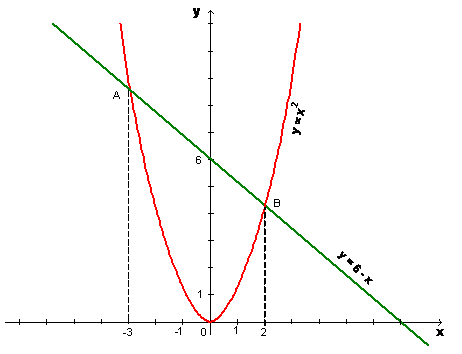
Получили две точки пересечения. Решением квадратного уравнения являются абсциссы этих точек х1 = – 3, х2 = 2. Ответ: – 3; 2. III. Фронтальный опрос - Что является графиком квадратичной функции?
- Скажите алгоритм построения графика квадратичной функции?
- Что называется квадратичным уравнением?
- Приведите примеры квадратичных уравнений?
- Запишите на доске свой пример квадратичного уравнения, Назовите, чему равны коэффициенты?
- Что значит решить уравнение?
- Сколько способов вы знаете графического решения квадратных уравнений?
- В чем заключается графические способы решение квадратных уравнений:
IV. Закрепление материала № 23.6 (а) На доске решают учащиеся первым, вторым, третьим способами. Класс решает четвертым – х2 + 6х – 5 = 0 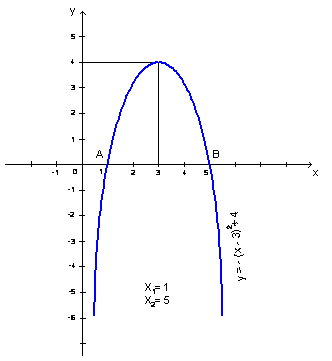
Преобразую квадратное уравнение, выделяя полный квадрат двучлена: – х2 + 6х – 5 = – (х2 – 6х + 5) = – (х2 – 6х + 32 – 9 + 5) = – ((х – 3)2 – 4) = – (х – 3)2 + 4 Получили квадратное уравнение: – (х – 3)2 + 4 = 0 Введем функцию: у = – (х2 – 3)2 + 4 Квадратичная функция вида у = а (х + L)2 + m Графиком явл. парабола, ветви направлены вниз, сдвиг основной параболы по оси Ох в право на 3 ед., по оси Оу вверх на 4 ед., вершина (3; 4). Строим по шаблону. Нашли точки пересечения параболы с осью Ох. Абсциссы этих точек явл. решением данного уравнения. х = 1, х = 5. Давайте посмотрим другие графические решение у доски. Прокомментируйте свой способ решения квадратных уравнений. 1 ученик Решение: 
– х2 + 6х – 5 = 0 Введем функцию у = – х + 6х – 5, квадратичная функция, графиком является парабола, ветви направлены вниз, вершина х0 = – в/2а х0 = – 6/– 2 = 3 у0 = – 32 + 18 = 9; точка (3; 9) ось симметрии х = 3 Строим по шаблону Получили точки пересечения с осью Ох, абсциссы этих точек являются решением квадратного уравнения. Два корня х1 = 1, х2 = 5 2 ученик Решение: – х2 + 6х – 5 = 0 Преобразуем: – х2 + 6х = 5 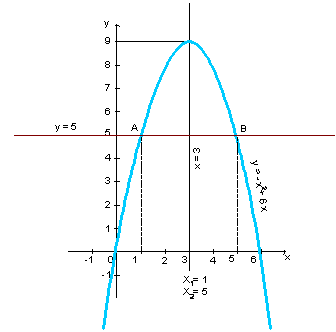
Введем функции: у1 = – х2 + 6х, у2 = 5, линейная функция, квадратичная функция, графиком графиком явл. прямая у || Ох явл. парабола, ветви направлены вниз, вершина х0 = – в/2а х0 = – 6/– 2 = 3 у0 = – 32 + 18 = 9; (3; 9). ось симметрии х = 3 Строим по шаблону Получили точки пересечения параболы и прямой, их абсциссы являются решением квадратного уравнения. Два корня х1 = 1, х2 = 5 Итак, одно и тоже уравнение можно решать различными способами, а ответ получаться должен один и тот же. V. Физкультминутка VI. Решение задачи с параметром № 23.19 При каких значениях р уравнение х2 + 6х + 8 = р: – Не имеет корней? – Имеет один корень? – Имеет два корня? Чем отличается это уравнение от предыдущего? Правильно, буквой! Эту букву в дальнейшем мы будем называть параметром, Р. Пока она вам ни о чем не говорит. Но мы будем в дальнейшем решать различные задачи с параметром. Сегодня решим квадратное уравнение с параметром графическим методом, используя третий способ с помощью параболы и прямой параллельной оси абсцисс. Ученик помогает учителю решать у доски. С чего начнем решать? 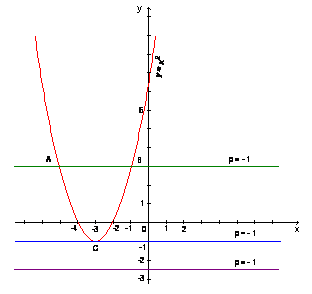
Зададим функции: у1 = х2 + 6х + 8 у2 = р линейная функция, квадратичная функция, графиком является прямая графиком явл. парабола, ветви направлены вниз, вершина х0 = – в/2а, х0 = – 6/2 = – 3 у0 = (– 3)2 + 6(– 3) + 8 = – 1 (– 3; – 1) Ось симметрии х = 3, таблицу строить не буду, а возьму шаблон у = х2 и приложу к вершине параболы. Парабола построена! Теперь надо провести прямую у = р. – Где надо начертить прямую р, чтобы получить два корня? – Где надо начертить прямую р, чтобы получить один корень? – Где надо начертить прямую р, чтобы не было корней? – Итак, сколько наше уравнение может иметь корней? – Понравилась задача? Спасибо за помощь! Оценка 5. VII. Самостоятельная работа по вариантам (5 мин.) I В. II В.
у = х2 – 5х + 6 у = – х2 + х – 6 Решить квадратное уравнение графическим способом, выбирая для вас удобный способ. Если кто-то справится с заданием раньше, проверьте свое решение другим способом. За это будет выставляться дополнительная оценка. VIII. Итог урока – Чему научились вы на сегодняшнем уроке? – Сегодня на уроке мы с вами квадратные уравнения решали графическим методом, используя различные способы решения, и рассмотрели графический способ решения квадратного уравнения с параметром! – Переходим к домашнему заданию. IХ. Домашнее задание 1. Домашняя контрольная работа на стр. 147, из задачника Мордковича по вариантам I и II. 2. На кружке, в среду, будем решать V-м способом, (гипербола и прямая).
| 
