Цели: - развивающие – познакомить с новым видом задач,
- познавательные – показать применение математики в жизни.
ХОД УРОКА Организационный момент: разбить класс на 3-4 группы (каждая группа должна быть разноуровневой, чтобы сильные ученики могли помочь остальным). В каждой группе на партах заранее лежат: лист 1 – карточки с устной работой (на каждого ученика); лист 2 – графы + задача; чистые листы для работы.
– Сегодня мы с вами познакомимся с новым видом задач, но сначала поработаем устно. – Скажите, какая фигура изображена у меня на рисунке? (Координатная прямая) – Как вы догадались, что это координатная прямая? (Начало отсчета, единичный отрезок, направление) – У вас на столах лежат задания к этой прямой. Определите координаты каждой точки и заполните пропуски. Впишите соответствующие буквы и получите два разных слова, которые будут иметь отношения к нашему уроку. 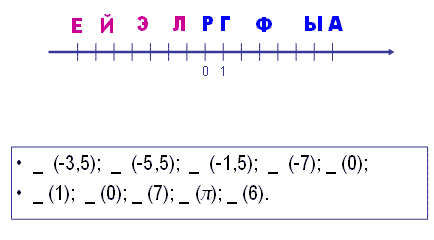
(Первый, кто выполнит задание идет к интерактивной доске заполнять пропуски). – Прочитайте слова. Какими числами являются координаты сиреневых букв? (Отрицательными) – А синих букв? Нуль? – Найдите среди координат противоположные числа. – Какие числа называются противоположными? – Почему одно число записано не цифрами, а буквой? – Чем оно заинтересовало математиков? – А знаете ли вы, что оно было известно еще в древности китайским математикам, Архимеду, но только в 18 веке Леонард Эйлер обозначил его буквой «П» для упрощения формул. Это первая буква в написании греческого слова «окружность» – «периферия».
– Леонард Эйлер – крупнейший математик 18 века – родился в Швейцарии, жил в нашем городе С-Петербурге по приглашению Петербургской Академии наук, считался современниками первым математиком мира, заложил основы теории графов, с помощью которых можно решать различные головоломки и математические задачи. – Мы познакомимся со знаменитой задачей, с которой началось изучение графов.
– Гуляя по Кенигсбергу (Калининград), Эйлер обратил внимание на расположение мостов через реку Преголь, их было 7. Жители города задали ему вопрос: можно ли совершить прогулку, пройдя по каждому мосту ровно один раз?
– Эйлер изобразил острова в виде точек, а мосты – это кривые. И построил первый граф. Итак, тема нашего сегодняшнего урока – «Графы».
– Граф – это набор точек, некоторые из которых соединены линиями. – Точки называются вершинами. – Соединяющие их линии называются ребрами графа. – Граф называется конечным, если число его ребер конечно, и бесконечным. – Мы будем рассматривать только конечные графы. – Сколько вершин и сколько ребер в каждом графе?
– Число ребер, выходящих из вершины графа, называют степенью этой вершины. – Вершина графа, имеющая нечетную степень, называется нечетной, а имеющая четную степень – четной. – Назовите степень каждой вершины. – Как связаны количество ребер и степени вершин? – Число нечетных вершин графа четно.
– Для того, чтобы найти количество ребер графа, нужно просуммировать степени вершин и полученный результат разделить на два. – Постройте графы, зная степени их вершин. – У вас на столах лежат листы бумаги, можете совещаться. - Построение первого графа. Команда, которая сделала первой, показывает свой граф на доске.
- Построение второго графа невозможно, т.к. сумма степеней вершин (5) не делится на 2.
– Граф называется связным, если его нельзя разбить на два, не разрывая в какой-нибудь вершине. В связном графе можно, двигаясь по ребрам, перейти из одной вершины в другую. – У вас на столах листы, на которых изображены пять фигур. 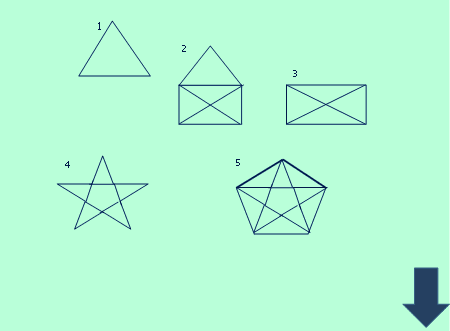
– Можно ли нарисовать фигуру одним росчерком, не отрывая карандаша от бумаги и не проводя по одной линии дважды? – Фигуры 1, 2, 4, 5 – можно (дети по очереди рисуют на доске); 3 – нельзя. – Определите степень каждой вершины. – Попробуем сделать вывод. Граф можно обойти, пройдя по каждому ребру только один раз в том случае, если граф связный и нечетных вершин у него 0 или 2. Если нечетных вершин нет, то маршрут может начаться в любой вершине и в ней же кончиться. При этом, если нечетных вершин две, то маршрут начинается в одной из них, а заканчивается в другой. Такие фигуры называются уникурсальными. – Вернемся к задаче с мостами.
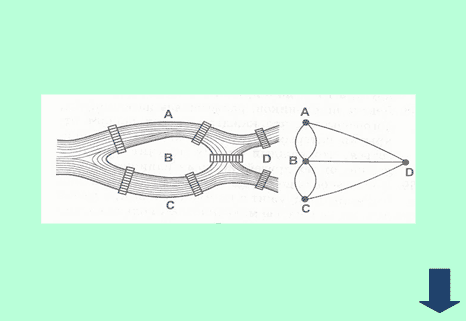
– Можно ли нарисовать фигуру одним росчерком, не отрывая карандаша от бумаги и не проводя по одной линии дважды? – Нет. Этот граф не является уникурсальной кривой, т.е. путешествие невозможно. Составление графов помогает решать задачи.

– Обозначим мальчиков большими буквами, а виды транспорта – маленькими. Учитель работает на доске вместе с классом. 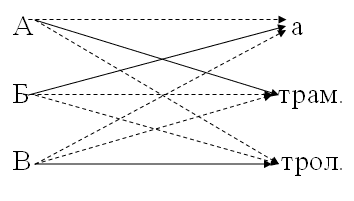
– Обязательно записываем все ходы решения, чтобы вы могли его восстановить и рассказать, как вы решали. А не на а А не на трол. А на трам. Б не в трол. Б на а В на трол.
– У вас в каждой группе задача, которую вы будете решать. – Можете приступать. – Обязательно обозначайте не только ребра, которые будут, но и пунктиром те ребра, которых точно не будет. Это поможет вам при решении задачи. 
Представитель группы, которая сделает раньше всех, записывает решение на доске. Ответ: Б – строитель А – тренер Г – врач В – журналист
– Графы используются в моделировании, экономике, планировании. – Где же мы встречаемся в жизни? – Типичный граф: схема линий метро. Вершины графа – станции. Ребра графа – пути между станциями. – Что нового узнали? – Что интересного? Домашнее задание: узнайте, где в нашем городе находится дом, в котором жил Леонард Эйлер?
| 
