Цель: проконтролировать знания, умения и навыки обучающихся по данной
теме.
Оборудование: интерактивная доска, ноутбуки у каждого ученика, ватман
(оценочная таблица).
Жюри: обучающиеся 11 класса.
Время проведения: 2 урока.
Зачет делится на два этапа. В основе первого лежит теоретический опрос
каждого обучающегося. Второй этап – решение разноуровневых задач.
Первый этап.
С помощью электронной доски и индивидуальных ноутбуков, обучающиеся выполняют
следующие задания:
Определить истинность утверждений:
| Если треугольник равносторонний, то каждая его медиана
одновременно и высота, и биссектриса. |
Истинно/Ложно |
| Если треугольник равнобедренный, то он и
равносторонний. |
Истинно/Ложно |
| Теорема – утверждение, которое принимается без
доказательства. |
Истинно/Ложно |
| В треугольнике можно провести три медианы. |
Истинно/Ложно |
| Если отрезок делит сторону треугольника пополам, то он
является медианой. |
Истинно/Ложно |
Количество верно выполненных заданий означало оценку, которую обучающиеся
получили за данное задание.
Среди пар данных треугольников найти пары равных треугольников. Ответ
обоснуйте.
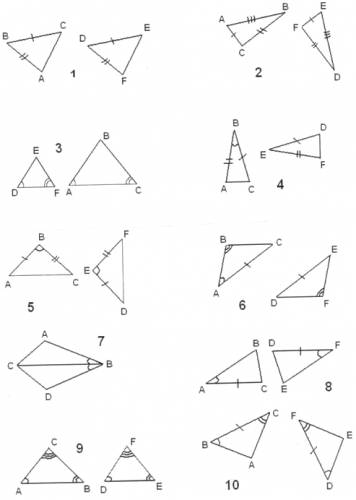
Второй этап.
Обучающиеся делятся на группы: сильный уровень, средний уровень, слабый
уровень. Каждой группе выдается практическая работа, решение которой они должны
будут защитить перед всем классом. Уровень А (слабые обучающиеся) проверяют
обучающиеся из уровня В, правильность решения задания уровня В проверяют
обучающиеся из уровня С. А задания уровня С проверяют старшеклассники.
А1) Треугольники АВС и МРК равны, если:
АВ=МР, АС=РК,  В= В= Р. Р.
АВ=МР, ВС=РК,  В= В= Р. Р.
АС=МК, ВС=РМ,  С= С= Р. Р.
СВ=КР,  В= В= М, М,  С= С= Р. Р.
А2) По второму признаку равенства треугольников
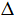 АВС= АВС=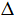 МРК,
если МРК,
если
АВ=МР, 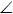 А= А=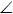 М, М,
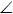 С= С=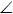 Р. Р.
АВ=РК, 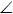 А= А=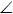 Р, Р,
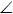 В= В=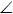 К. К.
АС=МК, 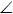 А= А=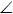 М, М,
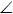 С= С=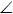 Р. Р.
ВС=РК, 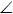 В= В=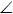 М, М,
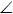 С= С=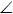 Р. Р.
А3) По третьему признаку равенства треугольников 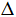 АВС= АВС=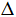 МРК,
если МРК,
если
АВ=МР, ВС=РК, АС=МК.
АВ=МР, ВС=РК, ВА=МК.
АВ=МР, ВА=РК, АС=МК.
АВ=МР, ВС=РК, АС=РК.
В1) В равных треугольниках АВС и МРК  А= А= М, М,  В= В= Р,
АВ=МР, ВС=5 см, АС=4 см, МР=6 см. Чему равен периметр Р,
АВ=МР, ВС=5 см, АС=4 см, МР=6 см. Чему равен периметр 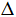 МРК? МРК? В2) Отрезки АВ и CD пересекаются в точке О так, что СО=DO,
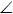 АСО= АСО=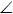 BDO,
АО=4 см. Чему равен отрезок ВО? BDO,
АО=4 см. Чему равен отрезок ВО? В3) В треугольниках АВС и МКЕ АВ=МК, ВС=КЕ, АС=МЕ, АВ=4 см, КЕ = 6 см, МЕ = 7
см. Чему равна разность АС и МК? С1) Отрезки АВ и CD пересекаются в точке О так, что АО=ВО, СО=DO, СО=5 см,
ВО=3 см, BD = 4 см. Чему равен периметр
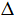 САО? САО?
- 15 см.
- 10 см.
- 12 см.
- 14 см.
Уровень В.
1) Известно, что 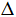 АВС= АВС=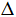 А1В1С1,
причем А1В1С1,
причем  А= А= А1, А1,  В=∠В1. На
сторонах АС и А1С1 отмечены точки D и D1 так,
что CD=C1D1. Какие из утверждений верны? В=∠В1. На
сторонах АС и А1С1 отмечены точки D и D1 так,
что CD=C1D1. Какие из утверждений верны?
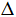 CBD= CBD=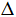 C1B1D1. C1B1D1.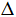 ABD= ABD=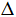 C1B1D1. C1B1D1.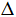 CAD= CAD=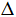 C1B1D1. C1B1D1.- CBA=
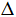 C1B1D1. C1B1D1.
2) Равные отрезки АВ и CD точкой пересечения О делятся пополам. BD=12 см, CD=16
см. Чему равна сторона АС? 3) На боковых сторонах АВ и ВС равнобедренного треугольника АВС отмечены
точки М и Р так, что АМ=СР, точка О лежит на стороне АС, углы АМО и СРО равны,
АС= 10 см. Чему равна длина отрезка СО? 4) По разные стороны от прямой АС отмечены точки В и D так, что ВАС= CAD, CAD,  ВСА= ВСА= DCA,
АВ=5 см, ВС= 8 см. Чему равна длина CD? DCA,
АВ=5 см, ВС= 8 см. Чему равна длина CD? 5) В четырехугольнике АВСD проведена диагональ АС, АВ=CD, ВС=AD. Периметр 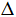 АВС=23 см, CD= 5 см, ВС= 8
см. Чему равна диагональ АС? АВС=23 см, CD= 5 см, ВС= 8
см. Чему равна диагональ АС?
Ответ: ____________.
6) По одну сторону от прямой АС отмечены точки В и К так, что АВ=СВ, АК=СК,  ВАС=82°, ВАС=82°,  КСА=39°. Чему
равен КСА=39°. Чему
равен  ВАК? ВАК?
Ответ: ____________.
1) Известно, что 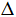 МКР= МКР=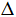 М1К1Р1,
причем М1К1Р1,
причем  М= М= М1, М1,  К= К= К1.
Найдите периметр К1.
Найдите периметр 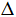 МКР, если
МК= 6 см и составляет три четверти отрезка К1Р1, а отрезок
МР на 3 см больше М1К1. МКР, если
МК= 6 см и составляет три четверти отрезка К1Р1, а отрезок
МР на 3 см больше М1К1.
Ответ: ________.
2) На биссектрисе угла АВС отмечены точки О и К (В-О-К) так, что углы АОК и
СОК равны. Периметр 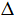 АВО=
17 см. ВА вдвое длиннее ВО и на 3 см больше СО. Найдите сумму длин отрезков ВС и
АО. АВО=
17 см. ВА вдвое длиннее ВО и на 3 см больше СО. Найдите сумму длин отрезков ВС и
АО.
Ответ: _______.
3) На стороне АС как на основании по разные стороны от нее построены два
равнобедренных треугольников АВС и АМС. Прямая ВМ пересекает сторону АС в точке
К. Найдите длину отрезка АК, если периметр
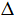 АВС равен 40 см, а его
боковая сторона на 7 см меньше основания. АВС равен 40 см, а его
боковая сторона на 7 см меньше основания.
Ответ: _________.
4) В равнобедренном треугольнике АВС с основанием ВС проведена медиана АМ.
Периметр 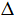 АВС равен 40 см,
а периметр АВС равен 40 см,
а периметр 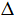 АВМ = 33 см.
Найдите длину медианы АМ. АВМ = 33 см.
Найдите длину медианы АМ.
Ответ: __________.
Задания второго этапа оцениваются по следующей оценочной шкале.
| |
А1 |
А2 |
А3 |
В1 |
В2 |
В3 |
С1 |
| № правильного ответа |
2 |
2 |
1 |
3 |
3 |
3 |
3 |
| Количество баллов |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
Оценка: менее 2 баллов – "2”, от 3 до 6 баллов – "3”, от 7 до 9 баллов –
"4”, от 10 до 12 баллов – "5”.
| |
1 |
2 |
3 |
4 |
5 |
6 |
| № правильного ответа |
1 |
2 |
4 |
2 |
10 |
43 |
| Количество баллов |
1 |
1 |
1 |
1 |
2 |
3 |
Оценка: менее 3 баллов – "2”, 4 балла – "3”, 6 баллов – "4”, 9 баллов –
"5”.
| |
1 |
2 |
3 |
4 |
| № правильного ответа |
23 |
13 |
9 |
13 |
| Количество баллов |
2 |
2 |
3 |
3 |
Оценка: менее 2 баллов – "2”, от 3 до 4 баллов – "3”, 7 баллов – "4”, 10
баллов – "5”.
Полученные результаты записываются в оценочную таблицу. И подводится итог.
| 
