Цели урока:
- подвести итог по изучению темы,
- проверить усвоенные знания,
- подготовка к контрольной работе.
Класс разбивается на 5 групп по 5 человек.
Старшими в группе назначаются успевающие
ученики (помощники учителя).
Ход урока
1 этап. Организационный момент. Постановка
целей
2 этап. Ответы на вопросы с использование
сигнальных карт (15 минут)
Каждой группе выдается путевой лист, в котором
помощники будут отмечать знание/незнание ответа
на вопрос. Каждому учащемуся выдаются две
карточки: зеленая и красная. Как только вопрос
сформулирован, ученики поднимают сигнальные
карты (знаю ответ – зеленая карточка, не знаю
ответ – красная карточка). Затем один ученик по
просьбе учителя вслух дает ответ на поставленный
вопрос.
Вопрос 1. Сформулируйте лемму о двух
коллинеарных векторах.
(Если векторы 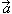 и и 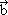 коллинеарны и коллинеарны и 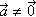 , то существует такое число k, что , то существует такое число k, что 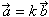 ). ).
Вопрос 2. Сформулируйте теорему о разложении
вектора по двум неколлинеарным векторам.
(Любой вектор можно разложить по двум данным
неколлинеарным векторам, причем коэффициенты
разложения определяются единственным образом).
Вопрос 3. Что такое координаты вектора?
(Это коэффициенты разложения вектора по
координатным векторам).
Вопрос 4. Сформулируйте правило нахождения
координат суммы векторов.
(Каждая координата суммы двух или более
векторов равна сумме соответствующих координат
этих векторов).
Вопрос 5. Сформулируйте правило нахождения
координат разности векторов.
(Каждая координата разности двух или более
векторов равна разности соответствующих
координат этих векторов).
Вопрос 6. Сформулируйте правило нахождения
координат произведения вектора на число.
(Каждая координата произведения вектора на
число равна произведению соответствующих
координат вектора на это число).
Вопрос 7. Напишите на доске формулу для
вычисления координат вектора по координатам его
начала и конца.
(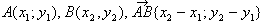 ) )
Вопрос 8. Напишите на доске формулу для
вычисления координат середины отрезка по
координатам его концов.
(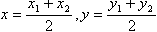 ) )
Вопрос 9. Напишите на доске формулу для
вычисления длины вектора по его координатам.
(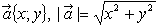 ) )
Вопрос 10. Напишите на доске формулу для
вычисления расстояния между двумя точками.
(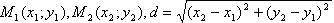 ) )
Вопрос 11. Напишите на доске уравнение
окружности данного радиуса с центром в донной
точке и уравнение окружности с центром в начале
координат.
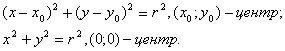
Вопрос 12. Напишите уравнение данной прямой в
прямоугольной системе координат.
(ax+by+c=0).
3 этап. Выполнение индивидуального задания (10
минут)
Каждому ученику выдаются задания, которые они
должны выполнить самостоятельно.
Примерные варианты карточек.
- Лежит ли точка A(2;-1) на окружности, заданной
уравнением
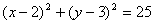 ? ? - Найдите длину вектора
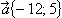 . . - Найдите координаты середины отрезка PQ, если P(5;-3),
Q(3;-7).
Карточка 2.
- Напишите уравнение окружности, если ее центр –
точка (4; 5), а радиус равен 3.
- Найдите координаты вектора
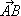 , если A(2;-5), B(-3;4). , если A(2;-5), B(-3;4).
- Напишите уравнение прямой, проходящей через
точку M(3;-2) и параллельной оси ординат.
Карточка 3.
- Напишите уравнение окружности с центром в точке
P(-2;-1), если она проходит через точку Q(1;3).
- Найдите координаты вектора
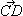 , если C(-1; 6), D(3; -2). , если C(-1; 6), D(3; -2).
- Найдите координаты вектора
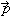 , если , если 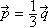 , а , а 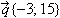 . .
4 этап. Групповое решение задачи (15 минут)
Каждой группе дается задача.
Даны координаты трех вершин параллелограмма KLMN:
K(-4; 2), L(0; 5), M(12; 0). Найдите координаты
четвертой вершины и периметр данного
параллелограмма.
Представитель группы, первой правильно
решившей задачу, объясняет решение у доски.
5 этап. Домашнее задание
| 
