Цели:

Оборудование: на доске портрет Карла Фридриха Гаусса , годы его жизни

I. Актуализация знаний

1. Найдите закономерность

В приведенной ниже таблице числа расположены в соответствии с определенной закономерностью. Установите эту закономерность и назовите число, которое следовало бы вписать в пустое место таблицы:

Ответ: 10.

2. Посмотрите на число и запомните:

26      101      418      2226.

Число убирается. Учащиеся должны по памяти воспроизвести число. Так как, число большое, то должны увидеть какую-то закономерность.

Ответ: Закономерность состоит в следующем: 2 6 10 14 18 22 26. Достаточно запомнить первое число, и к нему последовательно прибавлять число 4

II. Проверка домашнего задания

Числовой ребус:

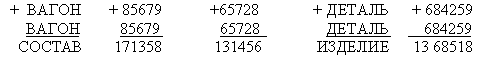
III. Вводное слово учителя

ЮНЫЕ МАТЕМАТИКИ

Истории математики известны случаи очень раннего проявления математических способностей. Французский ученый Блез Паскаль стал интересоваться математикой в столь раннем возрасте, что отец ему запретил ею заниматься. Однако, зайдя через некоторое время в детскую комнату, он обнаружил. Что мальчик углубился в рассмотрение какого-то рисунка из прямых линий и окружностей.
Очень рано раскрылись дарования и у Карла Гаусса, позднее ставшего одним из крупнейших математиков X IX века (его даже называли "царем математики”).
Рассказывают, что в возрасте трех лет он заметил ошибку, сделанную его отцом в расчетах. А семи лет мальчик пошел в школу. В то время в одной классной комнате занимались ученики разных классов. Чтобы занять первоклассников, пока он будет заниматься с третьим классом, учитель велел им сложить все числа от 1 до 100. Но не успел он закончить чтение условия задачи, как маленький Карл написал на своей грифельной доске ответ и положил на учительский стол.
С сожалением смотрел преподаватель на мальчика: ясно было, что за такой короткий срок он не мог сделать столько сложений. Остальные ученики терпеливо складывали. Когда учитель закончил занятия с третьеклассниками, он взял со своего стола грифельные доски. Ни у кого не было правильного результата. И только на доске Карла стоял ответ: 5050, причем никаких вычислений не было.
– Как же ты сосчитал? – спросил учитель.
– Очень просто, – ответил мальчик.
Как же вычислил маленький Гаусс?

– На этот вопрос нам и нужно сегодня ответить. И вычислить сумму так же быстро, как это сделал Гаусс.

Математический факт

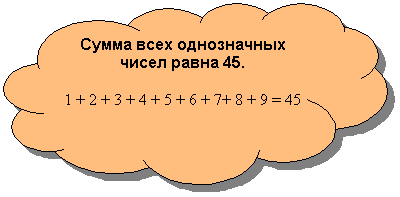
IV. Решение задач

Задача 1. Найдите сумму всех чисел от 1 до 10.

Учащиеся решают самостоятельно.

2-ой вариант решения:

+ 1  +  2  +  3  +  4  +  5   +  6  +  7  +  8  +  9 + 10
  10 +  9  +  8  +  7  +  6  +  5  +  4  +  3  +  2  +  1 
  11 + 11 + 11 + 11 + 11 + 11 + 11+ 11 + 11 + 11

Итак, получилось 10 пар, по 11, но так как числа брали 2 раза, то надо 10 : 2 = 5. Значит 11· 5 = 55.

Задача 2. Найдите сумму всех чисел от 1 до 20.

Решение:

Можно составить пары из чисел:

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + ... + 20 = (1 + 20) + (2 + 19) + (3 + 18) + (4 + 17) + (5 + 16) + (6 + 17 ) + (7 + 16) + ( 8 + 13) + (9 + 12) + (10 + 1) = 21 • 10 = 210

Задача 3.

Итак, собственно задача о нахождении суммы чисел от 1 до 100.

Решение:

+ 1 +   2   +   3   +   4   +   5   +   6   +   7  +   8   +   9   + 10  + ... + 100
100 + 99  +   98 +  97  +  96  +  95  +  94 +  93  +  92  + 91  + … +   1    
101+ 101 + 101 + 101 + 101 + 101 + 101+ 101 + 101 +101 + ...  + 101

В каждой сумме получилось по 110, но т.к. чисел всего 100, а брали их по два раза, значит их надо разделить на 2.

Задача 4. Найти сумму: 20 + 40 + 60 + … +  460 + 480 + 500.

Алгоритм:

1. Найдем сколько всего чисел в этой последовательности. Так как, здесь записана сумма чисел, которые делятся на 20, начиная с 20 до 500. Поэтому найдем их количество: 20 n = 500, n = 25. Всего 25 пар.
2. Найдем сумму первого и последнего числа: 20 + 500 = 520.
3. Вычислим непосредственно сумму по формуле:

Сумма чисел = (сумма (первого и последнего числа) · количество пар) : 2

(520 · 25) : 2 = 4160

Задача 5. Найти сумму: 30 + 60 + 90 + … + 540 + 570 + 600.

Решение:

1. 30 n = 600, n = 20
2. 30 + 600 = 630
3. 630 · (20 : 2) = 6300

Задача 6. Найти сумму: 6 + 12 + 18 + … + 90 + 96.

Решение:

1. 6 n = 96, n = 16
2. 6 + 96 = 102
3. 102 · (16 : 2) = 816

Задача 7. Найти сумму: 100 + 200 + 300 + … + 900 + 1000.

Решение:

1. 100 n = 1000, n = 10
2. 100 + 1000= 1100
3. 1100 · (10 : 2) = 5500

Задача 8. Найти сумму: 150 + 250 + 350 + … + 950.

Решение:

(150 + 950) + ( 250 + 850) + (350 + 750 ) + (450 + 650) + 550 = 1100 · 4 + 550 =   4950

1. 50 n = 950, n = 19. Но так как здесь сумма начинается не с 50, и не со 100, а со 150. Значит нужно исключить числа 50, 100, 200, 300, 400, 500, 600, 700, 800, 900. Их всего 10. 19 –10 = 9

2. 150 + 950 = 1100

3. 1100 · 9 : 2 = 4950

V. Итог урока

VI. Дополнительные задачи

1. Какой цифрой оканчивается сумма всех трехзначных чисел?

Решение:

100 + 101 + 102 + … + 998 + 999 = (101 + 999) + (102 + 998) + … + (549 + 551) + (100 + 550).

Каждая сумма в скобках оканчивается нулем. Поэтому сумма всех трехзначных чисел тоже оканчивается нулем.

2. Вычислите сумму всех нечетных чисел, находящихся в первой тысяче.

Решение:

1 + 2 + 3 + … + 997 + 999 = (1 + 999) + ( 3 + 997) + (5 + 995) + … + (499 + 501) = 1000 · 250 = 250000.

Всего чисел от 1 до 1000 – 1000 (тысяча), нечетных и четных наполовину. Значит нечетных чисел в первой тысяче 500. Пар слагаемых заключенных в скобки – 250.

3. Вычислите наиболее удобным способом: 99 – 97 + 95 – 93 +…+ 3 – 1

Решение:

Нечетных чисел в первой сотне 50. Всего пар слагаемых 25, значит (99 – 97) + (95 – 93) + … + (3 – 1) = 2 · 25 = 50

4. Вычислите наиболее удобным способом: 101 – 99 + 97 – 95 + 93 –… 5– 3 +1

Решение:

Нечетных чисел в первой сотне 50, но добавилось число 101, значит 51 нечетное число, но 1 не образовала пары, значит пар будет 25, и 1 отдельно (101 – 99 ) + (97 – 95) + (93 – 91) + … + (5 – 3) + 1 = 2 · 25 + 1 = 51.

5. Вычислите сумму: 1 + 1 + 2 + 3 + 5 +…+ 144 = ?

Решение:

Сначала нужно найти закономерность. Каждое следующее число равно сумме двух предыдущих. Например: 1 + 1 = 2, 1 + 2 = 3, 3 + 5 = 8 и т. д. Получаем следующую сумму: 1 + 1 + 2 + 3 + 5 + 8 + 13 + 21 + 34 + 55 + 89 + 144 = 377