Все «таинственные» свойства девятки объясняются тем простым фактом, что эта цифра является последней в употребляемой нами десятичной системе счисления. В восьмеричной системе счисления такими же любопытными свойствами обладает семерка. Это утверждение легко проверить. Прежде всего составим список шестнадцати чисел, обозначая их в восьмеричной системе, и выпишем рядом их эквиваленты в десятичной системе.

Предположим, что мы взяли число 341 (запись в восьмеричной системе) и вычли из него число 143, полученное обращением порядка записи цифр. Сначала отнимем 3 из 11. В десятичной системе это означало бы то же, что отнять 3 из 9. В ответе получилось бы 6. Но цифра 6 в обеих системах счисления обозначает одно и то же число, поэтому разность между 11 (запись в восьмеричной системе) и 3 равна 6. Продолжая далее вычитание этим же путем, получим в ответе 176 (запись в восьмеричной системе):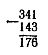

Вы замечаете, что цифрой, стоящей посередине, является семерка и что сумма крайних цифр тоже равна семи. Здесь происходит в точности то же самое, что и в варианте этого фокуса для десятичной системы, который мы описывали ранее, за исключением того, что ключевым числом является семерка, а не девятка.

Аналогичной проверке можно подвергнуть и все другие фокусы, основанные на свойствах девятки в десятичной системе. При этом для каждого из них найдется соответствующий фокус в восьмеричной системе, но роль «таинственного числа» будет принадлежать семерке. Выбирая соответствующую систему счислений, можно перенести особые свойства на любое желаемое число. Таким образом, становится очевидным, что эти свойства вытекают не из внутренних особенностей девятки, а только из того факта, что она является последней цифрой в нашей десятичной системе счисления.

Смешивание внутренних свойств числа с свойствами, вытекающими из его местоположения в данной системе счисления, является обычной ошибкой. Так, одно время думали, что по каким-то скрытым причинам среди цифр, изображающих бесконечную непериодическую десятичную дробь, обозначающую число я, семерка встречается в среднем реже других цифр. «Существует только одно число, настолько неравноправное среди других чисел, что невероятно, чтобы это могло быть случайностью, — писал доктор Огастес де Морган, — и это число есть таинственная семерка». Де Морган считал это, конечно, не всерьез; он хорошо знал, что цифры числа я в другой системе счисления будут совершенно отличными. В действительности даже в десятичной системе кажущейся редкость появления семерки в числе я объясняется ошибкой, допущенной Уильямом Шенксом при вычислении этого числа. В 1873 году, после пятнадцати лет упорного труда, Шенкс вычислил число π с семьсот семью десятичными знаками (ошибка, допущенная им на 528-м знаке, свела на нет все последующие вычисления). В 1949 году вычислительная машина ЭНИАК, так сказать, в виде отдыха от более сложных заданий вычислила π более чем с 2000 верными десятичными знаками. При этом никаких «таинственных» отклонений в частоте появления какой-нибудь цифры обнаружено не было[28]).