Данный урок разработан в форме зачета на два
урока.
Цель урока:
- повторение материала и проверка степени
усвоения материала по изученным темам
- развитие практических умений решения задач по
данной теме
- воспитание внимания, четкости и быстроты
мышления, аккуратности при построении чертежей.
Оборудование урока:
- раздаточный материал (20 карточек с задачами)
- модели и чертежи многогранников
- путевые листы для каждого ученика
- магнитофон
- плакаты с высказываниями о математике.
Весь проверяемый материал разбит на четыре
типа задач и теорию.
Стол 1: «Параллелепипед»
Стол 2: «Призма»
Стол 3: «Пирамида»
Стол 4: «Усеченная пирамида»
Стол 5: «Теория».
Все парты класса разбиты на пять групп с
определенным набором задач на каждом столе.
Каждый ученик получает свой путевой лист с
маршрутом: номер стола и вид задачи. На решение
задачи отводится определенное время, после
сигнала об окончании этого времени ученики
перемещаются по классу согласно своего маршрута.
Решенные задачи оставлены на столе, их собирает
учитель. Таким образом, ученик должен решить
четыре задачи и ответить на вопросы теории.
Карточки, помеченные красным цветом, получают
ученики с высоким уровнем знаний.
Карточки зеленого цвета – знания на «4»,
синие карточки получают ученики, обязательного
уровня обучения.
желтые карточки – минимум знаний.
Самое сложное заключается в том, чтобы
правильно рассадить учеников во время решения
задач. При увеличении количества учеников
необходимо добавить число задач на каждый стол.
Фамилия, имя |
Номер стола и вид карточки |
| 1. |
1 красный |
5 красный |
2 красный |
3 красный |
4 красный |
| 2. |
1 синий |
4 синий |
3 зеленый |
2 зеленый |
5 зеленый |
| 3. |
1 желтый |
2 зеленый |
5 желтый |
4 синий |
3 зеленый |
| 4. |
1 зеленый |
3 желтый |
4 зеленый |
5 красный |
2 зеленый |
| 5. |
2 красный |
4 красный |
1 зеленый |
3 зеленый |
5 красный |
| 6. |
2 желтый |
5 синий |
3 синий |
1 желтый |
4 синий |
| 7. |
2 синий |
1 желтый |
4 желтый |
5 синий |
3 синий |
| 8. |
2 зеленый |
3 зеленый |
5 красный |
4 красный |
1 зеленый |
| 9. |
3 красный |
5 зеленый |
4 красный |
2 красный |
1 красный |
| 10. |
3 зеленый |
2 красный |
1 красный |
4 желтый |
5 синий |
| 11. |
3 синий |
1 синий |
2 желтый |
4 зеленый |
5 желтый |
| 12. |
3 желтый |
4 желтый |
5 синий |
1 синий |
2 желтый |
| 13. |
4 красный |
3 красный |
5 зеленый |
2 желтый |
1 синий |
| 14. |
4 желтый |
5 желтый |
3 желтый |
1 зеленый |
2 синий |
| 15. |
4 зеленый |
2 синий |
1 желтый |
5 желтый |
3 желтый |
| 16. |
4 синий |
1 зеленый |
2 синий |
5 зеленый |
3 красный |
| 17. |
5 красный |
1 красный |
2 зеленый |
3 синий |
4 зеленый |
| 18. |
5 синий |
4 зеленый |
3 красный |
1 красный |
2 красный |
| 19. |
5 зеленый |
2 желтый |
1 синий |
3 желтый |
4 желтый |
| 20. |
5 желтый |
3 синий |
4 синий |
2 синий |
1 желтый |
Стол 1 «Параллелепипед»
 Стороны
основания прямого параллелепипеда равны 3 см и 5
см, уголмежду ними 120°. Большая диагональ
параллелепипеда равен Стороны
основания прямого параллелепипеда равны 3 см и 5
см, уголмежду ними 120°. Большая диагональ
параллелепипеда равен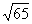 см.
Найдите длину бокового ребра и площадь полной
поверхности. см.
Найдите длину бокового ребра и площадь полной
поверхности.
 Стороны
основания прямого параллелепипеда равны 8 см и
10см. Одна из диагоналей основания 6см. Площадь
меньшего диагонального сечения Стороны
основания прямого параллелепипеда равны 8 см и
10см. Одна из диагоналей основания 6см. Площадь
меньшего диагонального сечения
36 см2. Найдите площадь боковой поверхности.
 Стороны
основания прямого параллелепипеда равны 4 см и
6см, боковое ребро 12 см. Найдите диагонали
параллелепипеда, угол наклона диагонали к
плоскости основания. Стороны
основания прямого параллелепипеда равны 4 см и
6см, боковое ребро 12 см. Найдите диагонали
параллелепипеда, угол наклона диагонали к
плоскости основания.
 В прямом
параллелепипеде высота равна 8 дм, стороны
оснований 7 дм и 24дм. Определить площадь
диагонального сечения. В прямом
параллелепипеде высота равна 8 дм, стороны
оснований 7 дм и 24дм. Определить площадь
диагонального сечения.
Стол 2 «Призма»
 Основанием
прямой призмы служит треугольник со сторонами 5,
5, 6 см. Высота призмы равна меньшей высоте
основания. Найдите площадь полной поверхности. Основанием
прямой призмы служит треугольник со сторонами 5,
5, 6 см. Высота призмы равна меньшей высоте
основания. Найдите площадь полной поверхности.
 В прямой
треугольной призме стороны основания
3,4,5см.Полная поверхность 84 см2.Определите
боковую поверхность и высоту. В прямой
треугольной призме стороны основания
3,4,5см.Полная поверхность 84 см2.Определите
боковую поверхность и высоту.
 Сторона
основания правильной четырехугольной призмы
15см, высота её 20см. Найдите площадь диагонального
сечения и площадь полной поверхности. Сторона
основания правильной четырехугольной призмы
15см, высота её 20см. Найдите площадь диагонального
сечения и площадь полной поверхности.
 В
правильной четырехугольной призме площадь
основания 144 см2, высота 14 см. Найдите
диагональ призмы. В
правильной четырехугольной призме площадь
основания 144 см2, высота 14 см. Найдите
диагональ призмы.
Стол 3 «Пирамида»
 Основание
пирамиды – треугольник со сторонами 10,10,16 см, все
боковые грани пирамиды наклонены к её основанию
под углом 45° . Найдите площадь полной
поверхности. Основание
пирамиды – треугольник со сторонами 10,10,16 см, все
боковые грани пирамиды наклонены к её основанию
под углом 45° . Найдите площадь полной
поверхности.
 Высота
пирамиды равна 16 см, площадь основания 512 см2.
На каком расстоянии от вершины находится
сечение, параллельное основанию, если площадь
сечения 50 см2. Высота
пирамиды равна 16 см, площадь основания 512 см2.
На каком расстоянии от вершины находится
сечение, параллельное основанию, если площадь
сечения 50 см2.
 Определите
апофему правильной треугольной пирамиды, если её
высота Определите
апофему правильной треугольной пирамиды, если её
высота
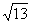 см, сторона основания
6см. см, сторона основания
6см.
 Высота
правильной четырехугольной пирамиды равна 7 см,
сторона основания 8 см. Найдите длину бокового
ребра. Высота
правильной четырехугольной пирамиды равна 7 см,
сторона основания 8 см. Найдите длину бокового
ребра.
Стол 4 «Усеченная пирамида»
 В
правильной усеченной четырехугольной пирамиде
стороны основания 8 см и 2 см. высота равна 4см.
Найдите полную поверхность. В
правильной усеченной четырехугольной пирамиде
стороны основания 8 см и 2 см. высота равна 4см.
Найдите полную поверхность.
 Стороны
оснований правильной усеченной треугольной
пирамиды 2 см и 6см. Боковая грань образует с
большим основанием угол 60°. Найдите высоту. Стороны
оснований правильной усеченной треугольной
пирамиды 2 см и 6см. Боковая грань образует с
большим основанием угол 60°. Найдите высоту.
 Высота
правильной четырехугольной усеченной пирамиды
равна 4 см, стороны оснований 2 см и 8 см. Найдите
площадь диагонального сечения. Высота
правильной четырехугольной усеченной пирамиды
равна 4 см, стороны оснований 2 см и 8 см. Найдите
площадь диагонального сечения.
 Найдите
боковое ребро правильной четырехугольной
усеченной пирамиды, если её высота Найдите
боковое ребро правильной четырехугольной
усеченной пирамиды, если её высота 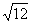 см, диагонали основания 6 см и 10
см. см, диагонали основания 6 см и 10
см.
Стол 5 «Теория»
 1. Дать
определение усеченной пирамиды. Покажите на
чертеже основание, высоту, апофему, ребра. 1. Дать
определение усеченной пирамиды. Покажите на
чертеже основание, высоту, апофему, ребра.
2. Сделайте вывод формулы для вычисления площади
боковой поверхности.
3. Что такое медианное сечение треугольной
пирамиды, усеченной четырехугольной пирамиды.
 1. Дать
определение пирамиды. Показать на чертеже
основание, высоту, боковые грани, апофему. 1. Дать
определение пирамиды. Показать на чертеже
основание, высоту, боковые грани, апофему.
2. Какая пирамида называется правильной?
3. Сформулируйте теорему о плоскости,
параллельной основанию пирамиды.
4. Запишите формулу для вычисления боковой
поверхности пирамиды.
5. Что является проекцией боковой ребра, апофемы
правильной пирамиды и как их найти.
 1. Что
такое параллелепипед (прямой, прямоугольный) 1. Что
такое параллелепипед (прямой, прямоугольный)
2. Перечислите все свойства параллелепипеда.
3. Как вычислить площадь его поверхности?
4. Что такое куб?
 1. Что
такое призма? (основания, боковые грани, высота,
диагональ, диагональное сечение) 1. Что
такое призма? (основания, боковые грани, высота,
диагональ, диагональное сечение)
2. Какая призма называется правильной?
3. Что такое боковая поверхность, полная
поверхность?
4. Запишите формулу для вычисления боковой
поверхности призмы.
5. Начертите призму.
| 
