Ключевые слова:

Зачем нужны графики и диаграммы

Невозможно быстро и качественно обрабатывать большие объёмы однотипной информации, представленной в текстовой форме. Такую информацию гораздо удобнее обрабатывать с помощью таблиц. Но восприятие громоздких таблиц также оказывается затруднительным для человека.

Предположим, вы готовитесь к школьной краеведческой конференции, на которой вам поручено нарисовать климатический портрет месяца мая. В течение всего месяца вы собирали информацию о температуре воздуха, давлении, влажности, облачности, направлении и скорости ветра. Соответствующую информацию вы заносили в заранее подготовленную таблицу, и вот что у вас получилось (табл. 13).

Таблица 13
Погода в мае 2012 года

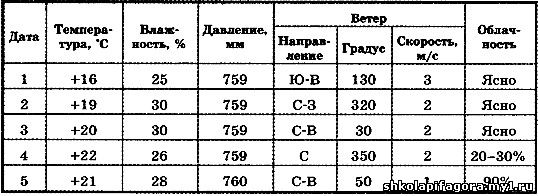
Конечно, можно перечертить эту таблицу на большой лист ватмана и продемонстрировать одноклассникам этот впечатляющий результат. Но смогут ли они воспринять эту информацию, обработать её и составить представление о погоде в мае? Скорее всего, нет.

Вы собрали большое количество информации, она точна, полна и достоверна, но в табличном виде не будет интересна слушателям, так как совершенно не наглядна. Сделать содержащуюся в таблице информацию более наглядной и легко воспринимаемой (визуализировать информацию) можно с помощью графиков и диаграмм.

Наглядное представление процессов изменения величин

На графике изображают две координатные оси под прямым углом друг к другу. Эти оси являются шкалами, на которых откладывают представляемые значения. Одна величина является зависимой от другой — независимой. Значения независимой величины обычно откладывают на горизонтальной оси (оси ОХ, или оси абсцисс), а зависимой величины — на вертикальной (оси OY, или оси ординат). При изменении независимой величины меняется зависимая величина. Например, температура воздуха (зависимая величина) может изменяться во времени (независимая величина). Таким образом, график показывает, что происходит с у при изменении х. На графике значения изображаются в виде кривых, точек или того и другого одновременно.

График позволяет отслеживать динамику изменения данных. Например, по данным, содержащимся во 2-м столбце таблицы 13, можно построить график изменения температуры в течение рассматриваемого месяца. По графику можно мгновенно установить самый тёплый день месяца, самый холодный день месяца, быстро подсчитать количество дней, когда температура воздуха превышала двадцатиградусный рубеж или была в районе +15°С. Также можно указать периоды, когда температура воздуха была достаточно стабильна или, наоборот, претерпевала значительные колебания (рис. 35).

Аналогичную информацию обеспечат графики изменения влажности воздуха и атмосферного давления, которые могут быть построены на основании 3-го и 4-го столбцов таблицы.

Изменение температуры воздуха в мае 2012 г.

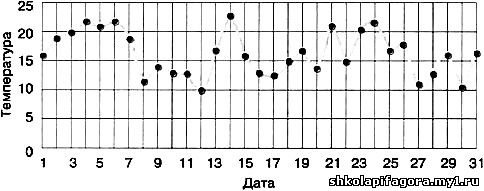
Рис. 35

Наглядное представление о соотношении величин

Теперь поработаем со столбцом «Облачность». По имеющимся данным очень трудно сказать, какая именно облачность преобладала в мае. Ситуация упрощается, если на основе имеющейся информации составить дополнительную таблицу, в которой представить количество дней с одинаковой облачностью (табл. 14).

Таблица 14
Облачность в мае 2012 г.

Наглядное представление о соотношении тех или иных величин обеспечивают диаграммы. Если сравниваемые величины образуют в сумме 100%, то используют круговые диаграммы.

На диаграмме (рис. 36) не указано количество дней с определённой облачностью, но показано, сколько процентов от общего числа дней приходится на дни с той или иной облачностью.

Дням с определённой облачностью соответствует свой сектор круга. Площадь этого сектора относится к площади всего круга так, как количество дней с определённой облачностью относится ко всему числу дней в мае. Поэтому, если на круговой диаграмме вообще не приводить никаких числовых данных, она всё равно будет давать некое примерное представление о соотношении рассматриваемых величин, в нашем случае — дней с разной облачностью.

Облачность в мае 2012 г.

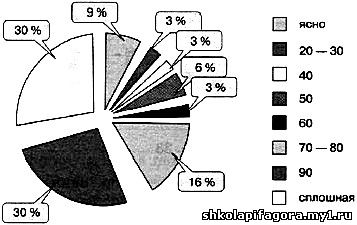
Рис. 36

Большое количество секторов затрудняет восприятие информации по круговой диаграмме. Поэтому круговая диаграмма, как правило, не применяется более чем для пяти-шести значений данных. В нашем примере эту трудность можно преодолеть за счет уменьшения числа градаций облачности: 0-30%, 40-60%, 70-80%, 90-100% (рис. 37).

Одного взгляда на диаграмму на рис. 37 достаточно для вывода о том, что в мае преобладали облачные дни, а ясных дней было совсем немного. Для обеспечения большей наглядности мы были вынуждены пожертвовать точностью.

Облачность в мае 2012 г.

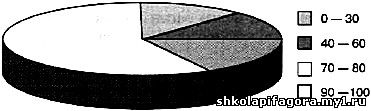
Рис. 37

Обеспечить и наглядность, и точность информации во многих случаях позволяют столбчатые диаграммы (рис. 38).

Облачность в мае 2012 г.

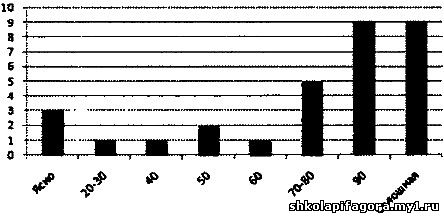
Рис. 38

Столбчатые диаграммы состоят из параллельных прямоугольников (столбиков) одинаковой ширины. Каждый столбик показывает один тип качественных данных (например, один тип облачности) и привязан к некоторой опорной точке горизонтальной оси — оси категорий. В нашем случае опорные точки на оси категорий — это фиксированные значения облачности. Высота столбиков пропорциональна значениям сравниваемых величин (например, количеству дней той или иной облачности). Соответствующие значения откладываются на вертикальной оси значений. Ни ось значений, ни столбики не должны иметь разрывов: диаграмму используют для более наглядного сравнения, и наличие разрывов уничтожает саму цель представления результатов в виде диаграммы.

По диаграмме на рис. 38 можно не только сравнить количество дней с той или иной облачностью, но и точно указать, сколько дней какой облачности было в течение рассматриваемого периода.

Если подсчитать количество дней с ветром каждого направления и на основании этой информации (табл. 15) построить лепестковую диаграмму, то мы получим так называемую розу ветров (рис. 39).

Таблица 15

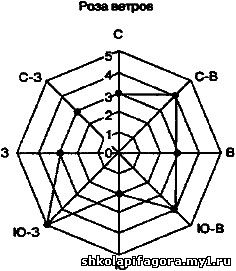
Рис. 39

Лепестковая диаграмма особенная, у неё для каждой точки ряда данных предусмотрена своя ось. Оси берут начало из центра диаграммы.