Но наедине с собой математика не всегда так уверена в себе. Она колеблется. Задает себе вопросы и порой сомневается в том, что они правильные. Особенно там, где дело касается бесконечности. Бесконечность может заставить математика бодрствовать ночами, вызывая тревогу, суетливость и чувство экзистенциального ужаса. В истории математики были времена, когда спущенная с привязи бесконечность была настолько взвинчена, что появлялись опасения, что она может все перевернуть с ног на голову.

В сериале «Клан Сопрано» босс мафии Тони Сопрано, страдающий приступами панических атак и пытающийся понять, почему его мать хочет, чтобы его убили, консультируется у врача-психиатра. Под напускной жесткостью скрывается очень смущенный и напуганный человек.

Таким же образом исчисление уложило себя на кушетку психиатра именно тогда, когда казалось, что оно при смерти. После многолетнего триумфа, уничтожив все проблемы, стоявшие на пути, оно начало осознавать что-то нездоровое, настораживающее в самой своей основе. Именно то, что сделало его успешным, — его жестокие навыки и бесстрашие в манипулировании бесконечными процессами — в настоящее время угрожало его уничтожить. И терапией, которая в конечном итоге помогла преодолеть этот кризис, стал, по случайному совпадению, анализ.

Вот пример одной из задач, которые волновали математиков XVIII века. Рассмотрим бесконечную сумму

1 — 1 + 1–1 + 1–1 +…

Это числовой эквивалент незатухающих колебаний: шаг вперед, шаг назад, шаг вперед, шаг назад и так далее до бесконечности.

Значит ли это, что данная последовательность чисел имеет какой-нибудь смысл? И если да, то чему она равна в результате?

Оптимист, дезориентированный бесконечно длинным выражением, подобным этому, может надеяться, что некоторые из старых правил, выкованных опытом взаимодействия с конечными суммами, останутся в силе. Например, мы знаем, что 1 + 2 = 2 + 1. Когда мы складываем два числа и более в виде конечной суммы, мы всегда можем поменять их порядок без изменения результата: a + b равно b + a (коммутативный закон сложения). И когда в выражении больше чем два члена, мы можем, поставив скобки, самозабвенно группировать его члены, не влияя на окончательный результат. Например: (1 + 2) + 4 = 1 + (2 + 4): сложение 1 и 2, а затем 4, дает тот же ответ, что и сложение 2 и 4, а затем 1. Это называется ассоциативным (сочетательным) законом сложения. Он работает, даже если суммируются несколько чисел. Мы знаем, что вычитание числа — то же самое, что прибавление отрицательного числа. Например, рассмотрим сумму, состоящую из первых трех членов записанного выше числового ряда, и зададим вопрос: что такое 1–1 + 1? Мы могли бы представить это как: (1–1) + 1 или 1 + (–1 + 1), где во втором выражении в скобках вместо вычитания 1 прибавляем –1. В любом случае ответ будет: 1.

Но когда мы попытаемся обобщить эти правила для бесконечных сумм, то столкнемся с несколькими неприятными сюрпризами. Посмотрите на возникающее противоречие: если мы возьмем ассоциативный закон и доверчиво применим его к 1–1 + 1–1 + 1–1 +… С одной стороны, мы можем сократить положительные и отрицательные единицы, группируя их следующим образом:

1 — 1 + 1–1 + 1–1 +… = (1–1) + (1–1) + (1–1) +… = 0 + 0 + 0 +… = 0.

С другой — можно точно так же, как здесь показано, поставить скобки и сделать вывод, что результат равен 1.

1 — 1 + 1–1 + 1–1 +… = 1 + (–1 + 1) + (–1 + 1) +… = 1 + 0 + 0 +… = 1.

Ни один из этих способов не кажется более убедительным, поэтому какова вероятность, что сумма равна и 0, и 1? Сегодня для нас это предположение звучит абсурдно, но в то время некоторые математики утешились его религиозным подтекстом. Он напоминал им о богословском утверждении, что Бог создал мир из ничего. Как написал в 1703 году математик и священник Гвидо Гранди: «Поставив по-разному скобки в выражении 1–1 + 1–1 +… я могу, если хочу, получить 0 или 1. Но тогда идея творения из ничего (лат. ex nihilo) совершенно правдоподобна».

Тем не менее очевидно, что Гранди предпочитал третье значение суммы, отличное от 0 или 1. Догадаетесь ли вы, какое именно? Подумайте, что можно сказать, если вы с ученым видом валяете дурака.

Правильно. Гранди считал, что истинная сумма равна . И великие математики, в том числе Лейбниц и Эйлер, были с ним согласны. Несколько линий рассуждения подтверждали этот компромисс. Например, 1–1 + 1–1 +… можно выразить с помощью собственных членов следующим образом. Давайте использовать букву S для обозначения суммы. Тогда по определению

S = 1–1 + 1–1 +…

Теперь оставим первую 1 в правой части уравнения в покое и займемся остальными его членами. Они создают собственную копию S, и члены, стоящие справа от первой 1, вычитаются из нее:

S = 1–1 + 1–1 +… = 1 — (1–1 + 1 —…) = 1 — S.

Так что S = 1 — S и, следовательно, S = .

Дебаты по поводу суммы 1–1 + 1–1 +… бушевали почти 150 лет, пока новое поколение аналитиков не водрузило все виды исчисления и его бесконечные процессы (пределы, производные, интегралы, бесконечные ряды) на прочный фундамент раз и навсегда. Они воссоздали предмет с нуля, выстроив строгую логическую структуру, как в Евклидовой геометрии.

Два основных понятия числового ряда — частичные суммы и сходимость. Частичная сумма представляет собой нарастающую сумму. Вы просто суммируете конечное число членов, а затем останавливаетесь. Например, если сложить первые три члена ряда 1–1 + 1–1 +… получим 1–1 + 1 = 1. Давайте назовем это S₃. Буква S обозначает «сумму», а индекс 3 показывает, что мы сложили только первые три члена. Вот несколько первых частичных сумм для этого ряда

S₁ = 1

S₂ = 1–1 = 0

S₃ = 1–1 + 1 = 1

S₄ = 1–1 + 1–1 = 0.

Таким образом, мы видим, что частичные суммы скачут между 0 и 1, и при этом не наблюдается никакой тенденции остановиться на 0, 1, или где-нибудь еще. По этой причине современные математики сказали бы, что сумма 1–1 + 1–1 +… не сходится.

Другими словами, частичные суммы не стремятся ни к какому предельному значению по мере увеличения числа членов, включенных в них. Поэтому сумма этого бесконечного ряда не имеет смысла.

Итак, мы придерживаемся прямой и узконаправленной линии поведения: не тратим впустую время и ограничиваемся анализом только тех рядов, которые сходятся. Значит ли это, что мы избежим встреченных ранее противоречий?

Пока нет. Кошмар продолжается. И это хорошо, что он существует, потому что напуганные им аналитики XIX века открыли более глубокие тайны в самом сердце исчисления, а затем вытащили их на свет. Извлеченные из этого уроки оказались бесценными не только для математики, но и для ее приложений во всех областях — от музыки до медицинской визуализации.

И если вы рассмотрите достаточно много таких сумм, то обнаружите, что они нацеливаются на число, близкое к 0,69. Действительно, можно доказать, что этот ряд сходится. Его предельное значение равно натуральному логарифму от 2 (обозначается ln2), приблизительно составляющему 0,693147.

Так что же здесь кошмарного? На первый взгляд, ничего. Знакочередующийся гармонический ряд походит на паиньку: сходящийся, с хорошим поведением. Ваши родители похвалили бы его.

Именно это и делает его опасным. Это хамелеон, мошенник, скользкий тип, который может быть кем угодно. Если переставлять его члены в произвольном порядке, вы можете подвести его сумму к любому значению. Буквально. Например, 297, 126 или –42π, или 0, или любому другому.

Это выглядит так, будто ряд полон презрения к коммутативному закону сложения. Просто просуммировав его члены в иной последовательности, вы можете изменить ответ, чего никогда не произошло бы с конечной суммой. Поэтому, даже если исходный ряд сходится, в нем по-прежнему будут странности, которые невозможно представить в обычной арифметике.

Вместо того чтобы доказать этот удивительный факт (результат, известный как теорема Римана о перестановке слагаемых в условно-сходящихся рядах), рассмотрим очень простую перестановку, сумму которой легко посчитать. Сгруппируем члены этого ряда таким образом, чтобы к каждому положительному слагаемому прибавлялось два отрицательных.

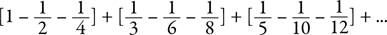
Далее упростим каждое выражение в скобках, вычитая второй член из первого и оставляя без изменения третий член. Тогда ряд сводится к сумме:

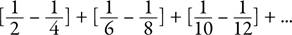
После вынесения за скобки из всех дробей выражения как общего множителя ряд примет вид:

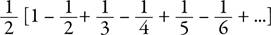
Смотрите, кто вернулся! Бестия в скобках — это снова знакочередующийся гармонический ряд. Но в результате перестановки, даже при сохранении всех его членов, как-то получилось, что он вдвое уменьшился по сравнению с первоначальным! Представленный в таком виде ряд теперь сходится к ln2 = 0,346…

Странно? Да. Ненормально? Да. Но неудивительно ли, что то же самое происходит и в реальной жизни. Как мы уже убедились в ходе прочтения книги, даже самые заумные и надуманные понятия математики часто находят практическое применение. Связь с практикой в данном случае заключается в том, что во многих областях науки и техники (от обработки сигналов и акустики до финансов и медицины) лучше всего представлять различные виды кривых, звуков, сигналов или изображений как группы (или совокупности) более простых кривых, звуков, сигналов или изображений. При этом основными строительными блоками будут синусоиды. Этот метод называется анализом Фурье, а соответствующая сумма — рядом Фурье. Но когда рассматриваемый ряд имеет некоторые патологические свойства, как у знакочередующегося гармонического ряда и его невменяемых родственников, сходимость у ряда Фурье может быть действительно очень необычной.

Вот, например, один из рядов Фурье, непосредственно вдохновленный знакочередующимся гармоническим рядом:

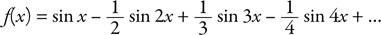
Чтобы получить представление о том, как он выглядит на графике, давайте рассмотрим сумму его первых десяти членов.

Частичная сумма 10 членов

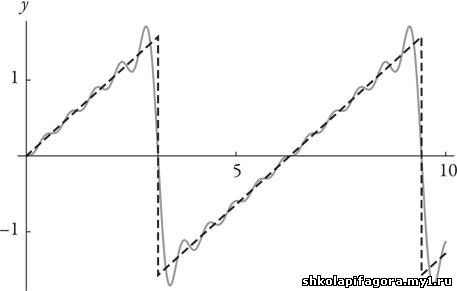
Эта частичная сумма (показана сплошной линией) явно пытается приблизиться к более простой волновой кривой в форме зубцов пилы (показано пунктирной линией). Заметим, однако, что вблизи краев зубцов что-то не так. Синусоида «промахнулась» и приняла вид странного пальца, который выходит за пилообразную волну. Чтобы увидеть это отчетливее, посмотрим на увеличение одного из зубцов при x = π:

Частичная сумма 10 членов

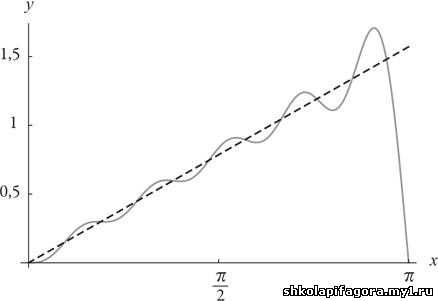
Попытаемся избавиться от пальца, включив в частичную сумму больше слагаемых. Не повезло. Палец просто становится тоньше и перемещается ближе к краю, но его высота остается примерно такой же.

Частичная сумма 50 членов

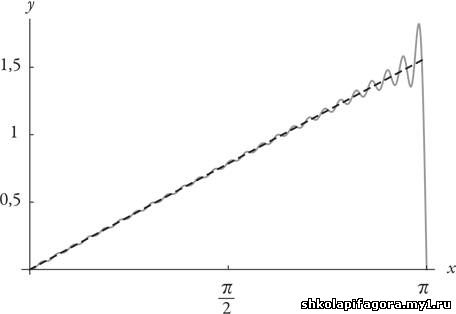
Частичная сумма 100 членов

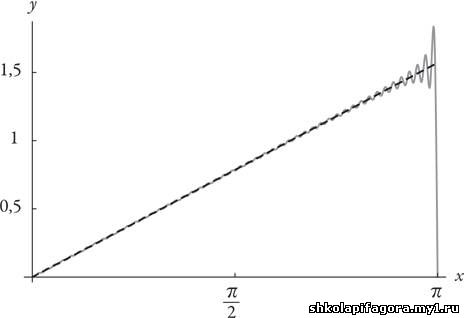
Вину за происходящее можно возложить на знакочередующийся гармонический ряд. Его описанная выше патология сейчас загрязняет ряды, связанные с рядами Фурье. Они отвечают за этот раздражающий палец, который никуда не денется.

Данный эффект, обычно называемый феноменом Гиббса, больше, чем просто математический курьез. Он известен с середины XIX века и в настоящее время проявляется в цифровой фотографии и на МРТ-сканировании. Нежелательные колебания, вызванные феноменом Гиббса, могут привести к размытости, мерцанию и прочим непреднамеренным нежелательным визуальным искажениям на острых краях видеоизображения. В медицинской практике их можно ошибочно принять за поврежденную ткань или скрыть повреждения, которые есть на самом деле.

К счастью, сто лет назад аналитики точно определили, что вызывает артефакты Гиббса (см. примечание), и научили нас, как преодолеть эти явления, или, по крайней мере, распознать их в случае появления.