В средней школе мы с друзьями обожали разгадывать классические головоломки. Что произойдет, если непреодолимая сила встретит неподвижный объект? Легко! Они взрываются. Обычная философия для тринадцати лет.

Но одна загадка долго волновала нас. Если вы продолжаете двигаться, находясь на полпути к стене, вы когда-нибудь до нее дойдете? Как-то очень грустно было думать, что ты все ближе и ближе к цели и все же никогда до нее не доберешься. (Наверное, это и есть метафора подростковой тоски по необъяснимому.) Еще одной проблемой было завуалированное присутствие бесконечности. Чтобы добраться до этой стены, следовало сделать бесконечное число шагов, и в конце они были бы бесконечно малой длины. Ух ты!

Вопросы, подобные этому, всегда вызывали головную боль. Около 500 года до н. э. Зенон Элейский сформулировал четыре парадокса бесконечности, которые озадачили его современников, что, возможно, отчасти послужило причиной изгнания данного понятия из математики на столетия. Например, в евклидовой геометрии рассматривалось только конечное число шагов. Считалось, что бесконечность неопределенна и непознаваема, и ее трудно сделать логически упорядоченной.

Но Архимед, величайший математик античности, осознал мощь бесконечности. Он заставил ее решать задачи, которые в противном случае были бы нерешаемы, и в процессе движения к бесконечности приблизился к изобретению интегрального исчисления — почти за 2000 лет до Ньютона и Лейбница.

В следующих главах мы рассмотрим великие идеи, лежащие в основе исчисления бесконечно малых. Но сейчас я хотел бы начать с первой из красивых идей, встречающихся у древних при вычислении площади круга и числа π.

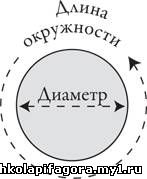
Давайте вспомним, что мы подразумеваем под «пи». Это отношение двух расстояний, где одно — диаметр (отрезок между наиболее удаленными точками окружности, проходящий через ее центр), а другое — длина окружности. «Пи» (π) определяется как отношение длины окружности к ее диаметру.

Если вы вдумчивый исследователь, то вас уже кое-что должно насторожить. Откуда мы знаем, что π имеет одинаковое значение для любых окружностей? Может быть, оно различно для больших и маленьких кругов? Ответ на этот вопрос отрицательный, но его доказательство не тривиально. Вот вам интуитивный аргумент.

Представьте, что с помощью ксерокса вы уменьшаете изображение круга, скажем, на 50 %. Тогда все расстояния на рисунке, в том числе длина окружности и ее диаметр, тоже уменьшатся на 50 %. Итак, когда вы разделите длину новой окружности на ее диаметр, уменьшение на 50 % нейтрализуется, и их соотношение останется неизменным. Оно и составляет π.

Конечно, здесь мы не сможем узнать величину π. Простые эксперименты с веревкой и блюдом достаточно хороши, чтобы получить значение около 3 или, если вы хотите более точный результат, 3 1/7. Но, предположим, надо найти значение π точно или приближенно, но с любой желаемой точностью. Что тогда? Эта проблема приводила древних в замешательство.

Прежде чем перейти к блестящему решению Архимеда, я должен упомянуть еще об одном случае, когда π появляется в связи с кругами. Площадь круга (размер пространства внутри него) вычисляется по формуле

A = πr²,

где A — площадь круга, π — греческая буква пи, а r — радиус окружности, определяемый как половина диаметра.

Все мы помним эту формулу из средней школы, но откуда она взялась? На уроках геометрии она обычно не доказывается. Если бы мы делали вычисления по ней, то, наверное, смогли бы найти доказательство. Но так ли уж необходимы вычисления, чтобы доказать ее?

Да, необходимы.

Задачу осложняет то, что эти фигуры имеют округлую форму. Если бы они были прямоугольными, проблемы бы не существовало. Найти площади треугольников и прямоугольников легко. А работать с такими изогнутыми формами, как круги, — трудно.

С математической точки зрения можно допустить, что изогнутая форма состоит из большого числа небольших прямоугольных отрезков. Это, конечно, не совсем так, но работает — при условии, что вы доведете их количество до предела, представив бесконечно много бесконечно малых частей. Это важнейшая идея всех вычислений.

Вот один из способов определить площадь круга. Начните с разбиения области на четыре равные части и переставьте их таким образом.

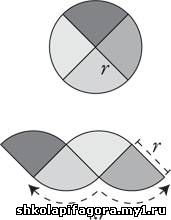
Странная форма с фестонами снизу имеет такую же площадь, как и круг, хотя это построение может показаться бесполезным, так как нам неизвестна площадь ее сегментов. Но по крайней мере мы знаем две важные вещи. Во-первых, две нижние дуги имеют общую длину, равную половине длины окружности исходного круга (потому что другая половина окружности приходится на две дуги сверху). Поскольку длина всей окружности в π раз больше диаметра, то ее половина в π раз больше половины диаметра, то есть радиуса r. Вот почему на рисунке показано, что πr — суммарная длина дуг фестонов в нижней части фигуры. Во-вторых, прямые стороны кусочков имеют длину r, так как каждая из них первоначально была радиусом окружности.

Далее повторим все описанные действия, но на этот раз уже с восемью отрезками круга.

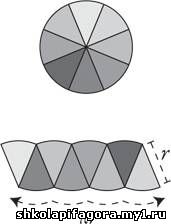
Теперь фигура приобрела менее странную форму. Дуги сверху и снизу по-прежнему существуют, но они не столь ярко выражены. Еще одно усовершенствование: левая и правая стороны изогнутой фигуры стали более вертикальными, чем раньше. Несмотря на все изменения, два факта остаются постоянными: дуги внизу по-прежнему имеют длину πr, а каждая сторона — длину r. И конечно, площадь фигуры та же — это площадь исходного круга, так как это просто фигура, составленная из восьми частей круга.

По мере увеличения числа отрезков происходит нечто чудесное: фестоны все больше и больше разглаживаются, превращая фигуру в прямоугольник. Дуги становятся более плоскими, а стороны — почти вертикальными.

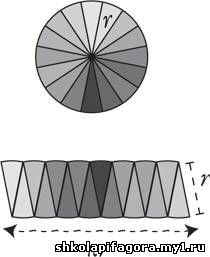
В пределе бесконечно большого числа частей фигура превратится в прямоугольник. Но, как и прежде, два факта все еще остаются неизменными: нижняя сторона прямоугольника равна πr, а высота — r.

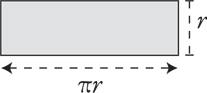
Но теперь задача упростилась. Площадь прямоугольника равна его ширине, умноженной на высоту, то есть произведение πr и r дает площадь прямоугольника, равную πr². А так как у преобразованной фигуры такая же площадь, как и у исходного круга, то полученное значение является также и площадью круга!

В таких расчетах приятно то, что бесконечность приходит на помощь. В каждом отдельном шаге фигуры с фестонами выглядели странными и бесперспективными. Но когда вы доходите до ее предела, она становится простой и красивой, и все проясняется. Вот так работает исчисление бесконечно малых в своем лучшем проявлении.

Архимед использовал подобную стратегию, чтобы приблизиться к π. Он заменил круг на многогранник с прямыми сторонами, а затем удваивал их число, чтобы приблизиться к идеальной округлости. Но вместо того чтобы согласиться на приближение неопределенной точности, он методично ограничивал π, поместив круг между вписанными и описанными многоугольниками, как показано ниже, на 6-, 12- и 24-сторонних фигурах.

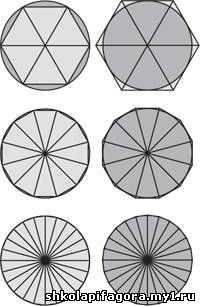
Затем с помощью теоремы Пифагора он выразил периметры этих внутренних и внешних многоугольников, начиная с шестигранника и далее для многоугольников с 12, 24, 48 сторонами, и в конечном итоге для 96-стороннего многоугольника. Формула для него позволила доказать, что

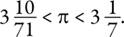
В десятичной системе счисления (которой у Архимеда не было) это означает, что π находится между 3,1408 и 3,1429.

Этот метод известен как метод исчерпывания, быть может, потому что неизвестные значения числа π загоняются между двумя известными числами, сжимающими его с двух сторон. Границы сужаются с каждым удвоением, тем самым исчерпывая возможности для маневра числа π.

В пределе бесконечно большого числа сторон многоугольников верхняя и нижняя границы неравенств будут сходиться к π. К сожалению, этот предел не такой простой, как у фигуры с фестонами, превратившейся в прямоугольник. Число π становится неуловимее, чем когда бы то ни было ранее. В настоящее время посчитано его значение более чем с 2,7 триллиона знаков, но вы никогда не будете знать его точно.

Помимо того что Архимед заложил основу для интегрального исчисления, он показал нам силу пошагового приближения. Прошло более двух тысячелетий, и эта стратегия развилась в современных методах численного анализа. Когда инженеры используют компьютеры для проектирования оптимально обтекаемого автомобиля или биофизики моделируют новый препарат химиотерапии в качестве защелки на раковую клетку, они используют численный анализ.

Математики и программисты, ставшие пионерами в области применения этого метода, создали высокоэффективные алгоритмы, которые можно выполнять миллиарды раз в секунду, что позволяет компьютерам решать задачи из всех областей современной жизни — от биотехнологий до Уолл-стрит и интернета. В каждом случае используется стратегия нахождения ряда приближений, сходящегося в пределе к правильному ответу.

И нет предела тому, где это можно применить.