Если вы были страстным любителем телевидения в 1980-х, то, конечно, помните сериал под названием «Детективное агентство "Лунный свет”» с живыми диалогами и романтическими отношениями между партнерами по фильму. В нем пару проницательных частных детективов Дэвида Эддисона и Мэдди Хэйс исполняли Брюс Уиллис и Сибилл Шепард.

В ходе расследования одного особенно жестокого дела Дэвид интересуется у помощника, кто ему кажется наиболее вероятным преступником. «Ума не приложу», — отвечает Мэдди. «А вы знаете, чего я не понимаю?» — спрашивает Дэвид. «Логарифмов?» — догадывается помощник. И Дэвид, реагируя на взгляд Мэдди, произносит: «А что? Вы их понимаете?»

Это довольно точно отражает всеобщее отношение к логарифмам. Большинство людей после окончания средней школы их никогда уже больше не используют, по крайней мере осознанно, и не обращают внимания на логарифмы, скрывающиеся за кулисами повседневной жизни.

То же самое касается и многих других функций, рассматриваемых в высшей математике и началах анализа. Степенные функции, показательные функции — в чем их суть? В этой главе я хочу помочь вам по достоинству оценить их полезность, даже если вам никогда не приходилось нажимать на кнопки инженерного калькулятора.

Математику необходимы функции по той же причине, что и строителю молотки и сверла. Инструменты преобразовывают вещи. То же самое делают функции. Поэтому математики часто обращаются к ним для выполнения преобразований. Но вместо дерева и стали функции обрабатывают числа и графики, а порой и другие функции.

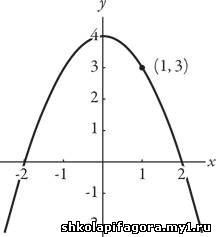
Чтобы понять, что я имею в виду, давайте построим график уравнения у = 4 — х². Возможно, вы помните, как это делается: сначала вы рисуете плоскость xy с горизонтальной осью х и вертикальной у. Затем для каждого значения х вычисляете соответствующее значение y; эта пара чисел является координатами одной точки графика на плоскости xy. Например, если х = 1, то уравнение говорит, что y = 4–1² = 4–1 = 3. Таким образом (х, у) = (1, 3) координаты точки. После того как вы вычислите и построите еще несколько точек на плоскости, возникнет следующая картина.

У нас получилась изогнутая математическими плоскогубцами кривая. В уравнении для у функция, которая преобразует x в x², ведет себя подобно обычному инструменту для сгибания материала. Когда ее прикладывают к любой точке на оси х (прямую от точки х до точки х² можно представить в виде прямого куска проволоки), плоскогубцы изгибают и вытягивают этот кусок проволоки в направлении вниз так, чтобы получилась изогнутая арка, как показано на рисунке.

А какую роль играет число 4 в уравнении у = 4 — x²? Это гвоздь, на который повесят картину на стену. Он поднимает изогнутые арки из проволоки на 4 единицы вверх. Так как при этом все точки кривой поднимаются на одинаковую высоту, то она считается постоянной функцией.

Данный пример иллюстрирует двойственный характер функций. С одной стороны, это инструменты: x² изгибает часть оси х, а 4 — ее лифт. С другой — строительные блоки: 4 и x² можно рассматривать как составные части более сложной функции 4 — х², точно так же, как провода, аккумуляторы и транзисторы — составные части радиоприемника.

Как только вы начинаете смотреть на мир подобным образом, сразу же везде замечаете функции. Описанная выше в виде арки кривая, в математике называемая параболой, — это автограф, который дала квадратичная функция за кулисами. Ищите ее, когда любуетесь струями фонтана. И если вам доведется побывать в международном аэропорту Детройта, обязательно остановитесь у фонтана терминала Delta, чтобы насладиться потрясающими резвящимися параболами.

Параболы и константы ассоциируются с более широким классом функций — степенными функциями вида xⁿ, в которых значение переменной x возводится в фиксированную степень n. Для параболы n = 2, для константы n = 0.

Разные значения n дают различные ручные инструменты. Например, возведение х в первую степень (n = 1) дает функцию, которая работает как пандус, отражая устойчивое увеличение роста или спада. Такая функция называется линейной, потому что ее графиком, построенным по точкам с координатами (x, y), является прямая линия. Если вы оставите на улице пустое ведро во время непрекращающегося ливня, то количество воды в нем будет расти линейно во времени.

Еще один полезный инструмент — обратно пропорциональная квадратичная функция у = 1/x², здесь n = –2. (Степень этой функции равна –2, так как x² стоит в знаменателе.) Эта функция хороша для описания затухания волн и ослабления сил в зависимости от расстояния х. Например, так затихает звук по мере удаления от источника.

Такие степенные функции служат строительными блоками, используемыми учеными и инженерами для описания роста и спада, которые происходят не слишком быстро. Но если нужен математический динамит, пора распаковать экспоненциальные функции. Они описывают все возможные быстропротекающие процессы — от цепных ядерных реакций до пролиферации бактерий в чашке Петри. Наиболее известный пример — функция у = 10^x, то есть 10 возведено в степень х. Не путайте ее с ранее рассмотренными степенными функциями. Здесь показатель (степень х) является переменной, а основание (число 10) постоянной, тогда как в степенной функции, подобной х², все наоборот. Такая перемена мест (переменной и константы) приводит к огромной разнице между этими функциями: при увеличивающемся значении x экспоненциальная функция с показателем x в конечном итоге растет быстрее любой степенной функции, независимо от ее степени. Экспоненциальный рост — невообразимо быстрый рост.

Вот почему так трудно сложить лист бумаги пополам больше семи-восьми раз. Каждое сложение листа удваивает его толщину, что приводит к ее (толщины) увеличению в геометрической прогрессии. В то же время длина, каждый раз сжимаясь пополам, уменьшается по экспоненциальному закону. После семи сложений толщина стандартного листа из записной книжки становится больше его длины, и поэтому дальше его складывать нельзя. Причем неважно, сколько усилий прикладывает человек при складывании. Предположим, лист можно сложить n раз — в результате стопка должна иметь 2ⁿ слоев. Здесь не может быть линейной зависимости, и еще одно сложение невозможно, если толщина стопки больше ее длины.

Задача считалась нерешаемой, пока в 2002 году Бритни Галливан, ученица старшего класса средней школы, не доказала обратное. Сначала она вывела формулу

L =  (2ⁿ + 4) (2ⁿ — 1),

которая позволяла посчитать максимальное количество сложений n, где Т — толщина листа бумаги, L — его длина, и складывается он только в одном направлении. Обратите внимание на запрещающее присутствие экспоненциальной функции 2ⁿ в двух местах: первый раз для учета удвоения толщины пачки при каждом сложении, а во второй — чтобы учесть двукратное сокращение ее длины.

Используя свою формулу, Бритни пришла к выводу, что ей понадобится специальный рулон туалетной бумаги почти в три четверти мили длиной. Она купила бумагу и в январе 2002 года отправилась в торговый центр в своем родном городе Помона, где и размотала ее. Семь часов спустя с помощью родителей девочка побила мировой рекорд, сложив бумагу двенадцать раз!

В теории также предполагается, что экспоненциальный рост увеличит ваш банковский счет. Если ваш вклад растет с годовой процентной ставкой, равной r, то через год сумма увеличится в (1 + r) раз от первоначального размера вклада; после двух лет она вырастет в (1 + r)² раз, а после х лет — в (1 + r)^х раз. Таким образом, чудо погашения долга, о котором мы так часто слышим, вызвано действием экспоненциального роста.

С этого места можно вернуться к логарифмам. Мы нуждаемся в них потому, что полезно иметь инструменты, которые могут отменить действие других инструментов. Подобно тому как каждый служащий нуждается как в степлере, так и в антистеплере, каждый математик нуждается как в показательных (экспоненциальных) функциях, так и в логарифмах, поскольку они взаимообратны. Это означает, что если вы введете в калькулятор число х и нажмете кнопку «10^х», а затем кнопку «log x», то в результате опять получите число х. Например, если х = 2, то 10^х составит 100. Взяв десятичный логарифм от 100, снова получим 2, так как log (100) = 2. Кроме того, log (1000) = 3, log (10 000) = 4, потому что 1000 = 10³, 10 000 = 10⁴.

Обратите внимание, в этом есть что-то магическое: как только числа внутри логарифмов увеличиваются мультипликативно каждый раз с десятикратным увеличением от 100 до 1000 и до 10 000 (то есть умножаются на 10), их логарифмы растут аддитивно, увеличиваясь от 2 до 3 и до 4. Наш мозг выполняет подобный трюк, когда мы слушаем музыку. Частоты нот в музыкальной гамме — до, ре, ми, фа, соль, ля, си — становятся нам слышны благодаря увеличению высоты звука равными интервалами. Но объективно их частоты растут, умноженные на равные множители. Мы же воспринимаем расстояние между высотой звука в гаммах «логарифмически».

Везде, где появляются логарифмы, — от шкалы Рихтера для определения магнитуды землетрясений до коэффициента кислотности рН, — они становятся замечательными «уплотнителями». Логарифмы идеально подходят для величин, изменяющихся в широком диапазоне, и сжимают их, чтобы они стали более управляемыми. Например, 100 и 100 000 000 отличаются в миллион раз — эту пропасть большинство из нас даже не может вообразить. Но их логарифмы разнятся всего в четыре раза (равны 2 и 8, так как 100 = 10² и 100 000 000 = 10⁸). Когда мы разговариваем о заработной плате, то используем грубую версию логарифмической краткости, определяя заработную плату в интервале между 100 000 и 999 999 долларов шестью цифрами. Эта «шестерка» является приблизительным логарифмом этих сумм заработной платы, которые на самом деле находятся в диапазоне от 5 до 6.

Поскольку только инструменты математика могут сделать так впечатляюще много, как описанные функции, возможно, именно поэтому я до сих пор не собрал купленные книжные шкафы.