Как и любое явление в жизни, арифметика имеет две стороны: формальную и занимательную (или игровую).

Формальную часть мы изучали в школе. Там нам объясняли, как работать со столбцами чисел, складывая и вычитая их, как перелопачивать их при выполнении расчетов в электронных таблицах при заполнении налоговых деклараций и подготовки годовых отчетов. Эта сторона арифметики кажется многим важной с практической точки зрения, но совершенно безрадостной.

С занимательной стороной арифметики можно познакомиться только в процессе изучения высшей математики. Тем не менее, она так же естественна, как и любопытство ребенка.

В эссе «Плач математика» Пол Локхарт предлагает изучать числа на более конкретных, чем обычно, примерах: он просит, чтобы мы представили их в виде некоторого количества камней. Например, число 6 соответствует вот такому набору камешков:

Вы вряд ли увидите тут что-то необычное. Так оно и есть. Пока мы не приступим к манипуляциям с числами, они выглядят примерно одинаково. Игра начинается, когда мы получаем задание.

Например, давайте посмотрим на наборы, в которых есть от 1 до 10 камней, и попробуем сложить из них квадраты. Это можно сделать только с двумя наборами — из 4 и 9 камней, поскольку 4 = 2 × 2 и 9 = 3 × 3. Мы получаем эти числа путем возведения в квадрат некоего другого числа (то есть раскладывая камни в виде квадрата).

Вот задача, имеющая большее число решений: надо узнать, из каких наборов получится прямоугольник, если разложить камни в два ряда с равным количеством элементов. Здесь подойдут наборы из 2, 4, 6, 8 или 10 камней; число должно быть четным. Если мы попробуем разложить в два ряда оставшиеся наборы с нечетным количеством камней, то у нас неизменно будет оставаться лишний камень.

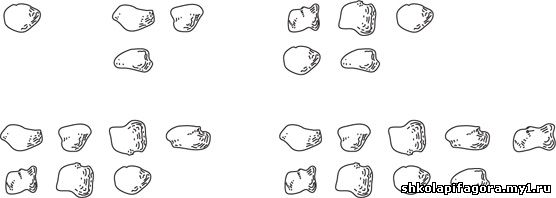
Но не все потеряно для этих неудобных чисел! Если взять два таких набора, то лишние элементы найдут себе пару, и сумма получится четной: нечетное число + нечетное число = четное число.

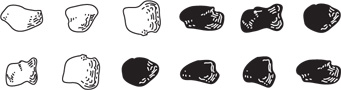
Если распространить эти правила на числа, идущие после 10, и считать, что количество рядов в прямоугольнике может быть больше двух, то некоторые нечетные числа позволят сложить такие прямоугольники. Например, число 15 может составить прямоугольник 3 × 5.

Поэтому хотя 15, несомненно, нечетное число, оно является составным и может быть представлено в виде трех рядов по пять камней в каждом. Точно так же любая запись в таблице умножения дает собственную прямоугольную группу камешков.

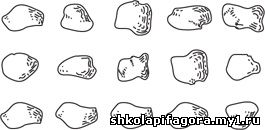
Но некоторые числа, вроде 2, 3, 5 и 7, совершенно безнадежны. Из них нельзя выложить ничего, кроме как расположить их в виде простой линии (одного ряда). Эти странные упрямцы — знаменитые простые числа.

Итак, мы видим, что числа могут иметь причудливые структуры, которые наделяют их определенным характером. Но, чтобы представить весь спектр их поведения, надо отстраниться от отдельных чисел и понаблюдать за тем, что происходит во время их взаимодействия.

Например, вместо того чтобы сложить всего два нечетных числа, сложим все возможные последовательности нечетных чисел, начиная с 1:

1 + 3 = 4

1 + 3 + 5 = 9

1 + 3 + 5 + 7 = 16

1 + 3 + 5 + 7 + 9 = 25

Удивительно, но эти суммы всегда оказываются идеальными квадратами. (О том, что 4 и 9 можно представить в виде квадратов, мы уже говорили, а для 16 = 4 × 4 и 25 = 5 × 5 это тоже верно.) Быстрый подсчет показывает, что это правило справедливо и для больших нечетных чисел и, видимо, стремится к бесконечности. Но какая же связь между нечетными числами с их «лишними» камнями и классически симметричными числами, образующими квадраты? Правильно располагая камешки, мы можем сделать ее очевидной, что является отличительной чертой изящного доказательства.

Ключом к нему будет наблюдение, что нечетные числа можно представить в виде равносторонних уголков, последовательное наложение которых друг на друга образует квадрат!

Подобный способ рассуждений представлен еще в одной недавно вышедшей книге. В очаровательном романе Ёко Огавы The Housekeeper and the Professor («Домработница и профессор») рассказывается о проницательной, но необразованной молодой женщине и ее десятилетнем сыне. Женщину наняли ухаживать за пожилым математиком, у которого из-за полученной черепно-мозговой травмы в краткосрочной памяти сохраняется информация только о последних 80 минутах жизни. Потерявшись в настоящем, один в своем убогом коттедже, ничего не имея, кроме чисел, профессор пытается общаться с домработницей единственным известным ему способом: спрашивая о размере ее обуви или дате рождения и ведя с нею светскую беседу о ее расходах. Профессор также питает особую симпатию к сыну экономки, которого называет Рут (Root — корень), потому что у мальчика сверху плоская голова, и это напоминает ему обозначение в математике квадратного корня .

Однажды профессор предлагает мальчику простую задачу — найти сумму всех чисел от 1 до 10. После того как Рут аккуратно складывает все числа между собой и возвращается с ответом (55), профессор просит его поискать более простой способ. Сможет ли он найти ответ без обычного сложения чисел? Рут пинает стул и кричит: «Это несправедливо!»

Мало-помалу домработница тоже втягивается в мир чисел и сама тайно пытается решить эту задачу. «Я не понимаю, почему так увлеклась детской задачкой, которая не имеет никакой практической пользы», — говорит она. «Сначала я хотела угодить профессору, но постепенно это занятие превратилось в сражение между мной и числами. Когда я просыпалась утром, уравнение уже ждало меня:

1 + 2 + 3 +. . + 9 + 10 = 55,

и весь день следовало по пятам, будто было выжжено на сетчатке моих глаз, и его никак не получалось проигнорировать». Существует несколько путей решения задачи профессора (интересно, сколько сможете найти вы). Профессор сам предлагает способ рассуждений, который мы уже применили выше. Он интерпретирует сумму от 1 до 10 в виде треугольника из камешков, с одним камешком в первой строке, двумя во второй и так далее, до десяти камешков в десятом ряду.

Эта картинка дает четкое представление о негативном пространстве. Оказывается, оно заполнено только наполовину, что показывает направление творческого прорыва. Если скопировать треугольник из камешков, перевернуть его и соединить с уже существующим, то получится нечто весьма простое: прямоугольник с десятью рядами по 11 камешков в каждом, причем общее число камней составит 110.

Так как исходный треугольник — половина этого прямоугольника, то вычисляемая сумма чисел от 1 до 10 должна быть половиной 110, то есть 55.

Представление числа в виде группы камешков может показаться необычным, но на самом деле так же старо, как и сама математика. Слово «вычислять» (англ. calculate) отражает это наследие и происходит от латинского calculus, означающего «галька», которую римляне использовали при выполнении вычислений. Чтобы получать удовольствие от манипуляций с числами, не обязательно быть Эйнштейном (что по-немецки означает «один камень»), но, возможно, умение жонглировать камешками облегчит вам это занятие.