Задуманная в Индии, Китае, Египте и Вавилоне более 2500 лет назад, систематизированная и уточненная Евклидом и древними греками, эта геометрия, построенная на представлении о плоской Земле, — основная (и зачастую единственная), которой сегодня учат в старших классах средней школы. Но ведь за последние несколько тысячелетий многое изменилось.

В эпоху глобализации, интернета и межконтинентальных воздушных путешествий всем необходимо иметь представление о сферической геометрии и ее современном обобщении, дифференциальной геометрии. Основным идеям последней около 200 лет. Своим возникновением она обязана Карлу Гауссу и Бернхарду Риману. Дифференциальная геометрия подводит фундамент под такое величественное интеллектуальное здание, как общая теория относительности Эйнштейна. В ее основе лежат красивые концепции, и они могут быть постигнуты каждым, кто когда-либо ездил на велосипеде, смотрел на глобус или растягивал резиновый шнур. Их понимание поможет вам разобраться в нескольких курьезах, которые вы могли заметить во время своих путешествий.

Например, когда я был маленьким, папа любил задавать мне загадки по географии. «Что севернее, — спрашивал он, — Рим или Нью-Йорк?» Большинство людей думают, что Нью-Йорк, но удивительно, оба города находятся почти на одной широте, причем Рим даже немного севернее. На обычной карте мира (где из-за ошибочности меркаторовой проекции Гренландия выглядит гигантской) кажется, что, двигаясь на восток, можно попасть прямо из Нью-Йорка в Рим. Тем не менее пилоты никогда не летят по этому маршруту. Из Нью-Йорка они всегда летят на северо-восток, придерживаясь побережья Канады. Раньше я думал, они это делают из соображений безопасности, но оказалось, был не прав. Просто с учетом кривизны Земли это самый прямой маршрут. Кратчайший способ добраться из Нью-Йорка в Рим — пролететь вдоль канадской провинции Новая Шотландия и Ньюфаундленда, далее проследовать над Атлантикой и наконец, пройдя к югу от Ирландии и пролетев всю Францию, достичь солнечной Италии.

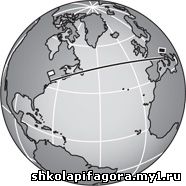
Такой путь называется дугой большой окружности. Как и прямые в обычном пространстве, большие окружности на сфере содержат кратчайшие пути между любыми двумя точками. Яркие примеры больших окружностей — экватор и меридиональные окружности, проходящие через Северный и Южный полюс.

Еще одно свойство, общее для больших окружностей и прямых, заключается в том, что это самые прямые и короткие пути между двумя точками. Возможно, это звучит странно, поскольку все пути на глобусе кривые, так что же тогда подразумевается под «прямой»? Нетрудно заметить, что на шаре одни кривые более изогнуты, чем другие. Кривизна больших окружностей обусловлена лишь тем, что она вынуждена повторять изогнутость поверхности сферы.

Чтобы понять это, представьте, что вы едете на крошечном велосипеде по поверхности шара и пытаетесь не сбиться с определенного пути. Если это часть большой окружности, то переднее колесо велосипеда все время будет направлено строго прямо вперед. Вот в таком смысле большие окружности прямые. В противоположность этому, если вы попытаетесь ехать вдоль линии широты вблизи одного из полюсов, вам придется постоянно держать руль повернутым в сторону полюса.

Конечно, ни одна реальная поверхность не может состоять только из простых плоскостей и сфер. Например, человеческое тело, консервная банка или бублик имеют различного рода отверстия и проходы, которые делают запутанными передвижения по таким поверхностям. В этой ситуации задача поиска кратчайшего пути между любыми двумя точками становится чрезвычайно сложной. Поэтому, вместо того чтобы искать технические решения, применим интуитивный подход. Вот где пригодятся резиновые шнуры.

Представьте скользкий упругий резиновый шнур, который максимально сжимается, оставаясь на поверхности объекта. С его помощью легко определить кратчайший путь между Нью-Йорком и Римом или, в случае необходимости, между любыми двумя точками на любой поверхности. Прикрепите концы шнура к точкам отправления и прибытия и позвольте ему растянуться, но так, чтобы он повторял контур поверхности. Когда шнур растянется настолько, насколько позволяет резина, — вуаля! — получится след кратчайшего пути.

На более сложных поверхностях, чем плоскости или сферы, может произойти нечто необычное: между двумя точками в локальной области может существовать множество кратчайших путей. Например, рассмотрим поверхность жестяной банки из-под консервированного супа с двумя точками, лежащими прямо друг под другом.

Кратчайшим путем между этими точками, как показано выше, явно будет отрезок, и наш упругий резиновый шнур нашел бы это же решение. Тогда что же здесь необычного? Цилиндрическая форма консервной банки открывает новые возможности для разного рода деформаций. Предположим, нам нужно, чтобы, прежде чем оказаться в конечной точке, шнур один раз опоясал консервную банку. (Подобное ограничение накладывается на спираль ДНК, когда она оборачивается вокруг определенных белков в хромосомах.) В этом случае шнур, натягиваясь, образует спираль, подобную спирали на торговых знаках парикмахеров.

Такая спиралевидная траектория рассматривается как еще одно решение в задаче о кратчайшем пути в том смысле, что это кратчайший из близлежащих путей. Если немного сдвинуть шнур, то он обязательно станет длиннее, а затем снова натянется и вернется в исходное положение. Можно сказать, что этот кратчайший путь — местный чемпион среди всех путей при однократном обертывании шнура вокруг цилиндра. (Кстати, именно поэтому данная область математики называется «дифференциальной геометрией». Она изучает влияние малых локальных различий (англ. differences) на такие характеристики геометрических объектов, как разность в длине между близлежащими спиралевидными путями.)

Но это еще не все. Есть еще один чемпион, который появится, если обвить шнуром банку дважды, и еще один, если обвить банку трижды, и так далее. На цилиндре существует бесконечное множество локальных кратчайших путей! Но ни один из них не является самым кратчайшим. Прямолинейный путь короче всех других.

Поверхности с отверстиями и ручками имеют много локально кратчайших путей, отличающихся рисунком их переплетения вокруг различных частей поверхности. Следующий стоп-кадр из видео математика Конрада Полтье из Свободного университета Берлина иллюстрирует неоднозначность этих локальных кратчайших путей, то есть геодезических линий, на поверхности придуманной планеты в форме восьмерки, которую специалисты называют тором с двумя отверстиями.

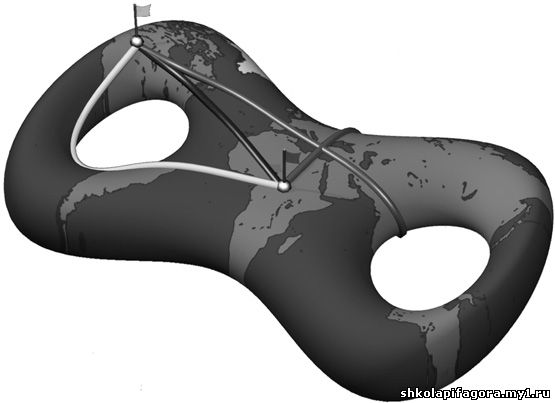
Три показанные здесь геодезические линии различной формы проходят по разным частям планеты, но их объединяет то, что они самые короткие по сравнению с близлежащими путями. И так же, как прямые линии на плоскости или большие окружности на сфере, эти геодезические линии — самые прямые из возможных кривых на поверхности. Они огибают ее, но не перегибаются сами. Чтобы пояснить это, Полтье сделал еще одно учебное видео.

Мотоцикл без водителя едет по геодезическому шоссе, повторяющему рельеф тора с двумя отверстиями. Примечательно, что руль заблокирован так, чтобы мотоцикл двигался только прямо и не мог съехать с дороги. Поэтому нет необходимости им управлять. Это усиливает уже сложившееся мнение о том, что геодезические линии, как и большие окружности на сфере, представляют собой естественное обобщение прямых линий.

После такого буйства фантазии вам, возможно, будет интересно узнать, есть ли у геодезических линий что-либо общее с реальностью. Конечно есть. Эйнштейн доказал, что, когда лучи света движутся по Вселенной, они перемещаются по геодезическим линиям. Знаменитый изгиб света звезд вокруг Солнца, обнаруженный при наблюдении солнечного затмения 1919 года, подтвердил, что свет движется по геодезическим линиям искривленного пространства-времени в соответствии с деформацией, вызванной притяжением Солнца.

На более приземленном уровне математика поиска кратчайших путей имеет решающее значение для маршрутизации трафика в интернете. Однако пространство всемирной сети, в отличие от гладких поверхностей, рассмотренных выше, — это гигантский лабиринт адресов и ссылок, а математические задачи о кратчайших путях трансформированы в задачи нахождения самых быстрых путей. Учитывая множество потенциальных маршрутов, их решение было бы невозможным, если бы изобретательность математиков и компьютерщиков не упростила его.

Иногда люди используют утверждение «кратчайший путь между двумя точками — это прямая линия» в переносном смысле, подтверждая тем самым присутствие здравого смысла. Другими словами, «не усложняй без необходимости». Но преодоление пути с препятствиями способно поднять до больших высот, поэтому и в искусстве, и в математике часто стоит наложить на себя определенные ограничения. Сочиняйте хайку и сонеты или расскажите историю своей жизни всего в шести словах. То же самое верно для всех направлений математики, призванных помочь вам найти кратчайший путь решения той или иной задачи, которую задает вам жизнь.

Две точки. Много путей. Математический экстаз.