Друг моего отца по имени Дэйв, выйдя на пенсию, поселился в городке Юпитер во Флориде. Когда мне было лет двенадцать, мы всей семьей гостили у него, и он показал нам то, что произвело на меня неизгладимое впечатление.

Дэйву нравилось составлять график времени наступления рассветов и закатов, которые он наблюдал в течение всего года. Каждый день он отмечал две точки на своем графике и после многих месяцев наблюдений заметил нечто любопытное. Эти две кривые выглядели как встречные волны. Когда одна из них поднималась, другая опускалась, а когда восход солнца наступал раньше, заходило оно позже.

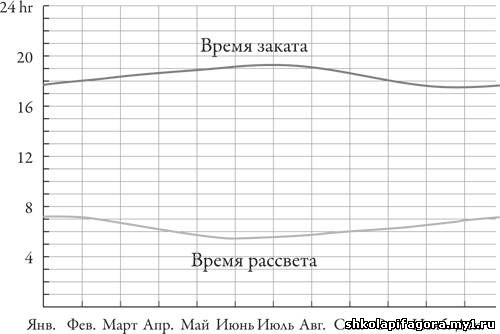
Но были и исключения. В последние три недели июня, большей части декабря и в начале января время наступления восхода и захода каждый день было одинаково более поздним, что придавало волнам слегка однобокий вид.

Тем не менее закономерность в поведении кривых казалась очевидной: изменение промежутка между ними показывало увеличение или уменьшение продолжительности дня в различные времена года. Путем вычитания значений нижней кривой из значений верхней Дэйв также выяснил, как в течение года меняется продолжительность светового дня. К его удивлению, в этой кривой вообще не было однобокости. Она выглядела абсолютно симметричной.

Он увидел почти идеальную синусоиду. Если вы проходили тригонометрию в средней школе, то, возможно, помните, что рассказывали о ней. Хотя не исключено, что ваш учитель больше говорил о синусоиде как об основном инструменте количественного выражения отношения между сторонами и углами треугольника. Это исходные тригонометрические определения древних астрономов и геодезистов.

Тем не менее тригонометрия, опровергая свое слишком скромное название, в настоящее время выходит далеко за рамки измерения треугольников. С помощью количественного описания круга она также проложила путь анализу всех повторяющихся с определенной частотой явлений — от океанских волн до волн головного мозга. Это ключ к математике циклов.

Чтобы увидеть, как тригонометрия соединяет круги, треугольники и волны, представьте, что маленькая девочка катается круг за кругом на колесе обозрения.

Оказывается, они с мамой интересуются математикой, поэтому решили, что такое катание — прекрасная возможность для эксперимента. Девочка взяла с собой GPS-навигатор, чтобы каждое мгновение регистрировать высоту, на которой находится: и в самой высокой точке, и при движении обратно вниз к земле, и снова, двигаясь вверх и вниз. Результаты выглядят следующим образом:

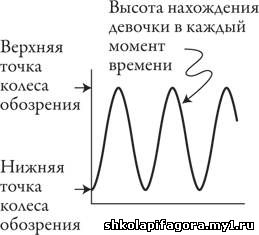
Это синусоида. Она возникает всякий раз, когда кто-нибудь или что-нибудь движется по горизонтали или вертикали и одновременно по кругу.

На уроках тригонометрии вы обсуждали, как синусоидальная волна связана с синусоидальной функцией? Ну, хорошо, допустим, мы рассматриваем снимок девочки. В запечатленный момент она находится под некоторым углом, назовем его a, по отношению к пунктирной линии на рисунке.

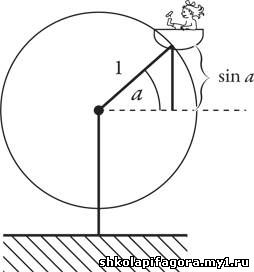
Отметим, что гипотенуза прямоугольного треугольника и радиус колеса обозрения имеют равную длину. Тогда sin a (читается синус a) показывает нам, на какой высоте находится девочка. Точнее, sin a определяется высотой, на которой она пребывает, измеренной от центра колеса с учетом того, что девочка находится под углом a к пунктирной линии.

По мере вращения колеса обозрения угол a будет постепенно увеличиваться и в конце концов превысит 90°, и с этого момента мы больше не сможем его рассматривать как угол прямоугольного треугольника. Означает ли это, что тригонометрию далее нельзя применять?

Нет. Испугавшись, как обычно, математики просто расширили область определения синусоидальной функции до любого угла, а не только для углов менее 90°, а затем представили sin a как высоту расположения девочки выше или ниже центра круга.

График sin a продолжает расти, а затем убывать (и даже становится отрицательным) — это то, что мы подразумеваем под синусоидой. Такие колебания повторяются на протяжении каждых 360°, что соответствует полному обороту.

Такой способ трансформации кругового движения в синусоиду часто встречается в повседневной жизни, хотя не всегда заметен для нас. Гул люминесцентных ламп над головой в наших офисах напоминает, что где-то в энергосистеме генераторы вращаются со скоростью 60 оборотов в секунду, преобразуя свое вращательное движение в переменный ток, то есть в электрические синусоидальные волны, от которых во многом зависит современная жизнь. Когда вы говорите, а я вас слушаю, органы наших тел используют синусоиды: вашего — при генерации звука путем вибраций голосовых связок, а моего — посредством колебаний волосков в ушах, принимающих звуки голоса. Если мы откроем наши сердца этим синусоидам и настроимся на их молчаливый напев, то у них появится сила сдвинуть нас. В этом есть нечто мистическое.

Когда рвется гитарная струна или дети крутят скакалку — во всех этих случаях проявляются синусоиды. Круги на поверхности пруда, гребни дюн, полосы зебры — все это отражение основного механизма формирования закономерностей природы, появления синусоидальной структуры на основе повторяемости.

Эти явления обусловлены существованием глубинных математических механизмов. Всякий раз, когда по какой-то причине теряется устойчивость некоего состояния равновесия в физических, биологических или химических процессах, первыми появляются синусоиды или их сочетания.

Синусоиды — это атомы структуры. Они — блоки мироздания природы. Без них не было бы ничего, что придавало бы новый смысл латинскому выражению sine qua non — это «непременное условие».

Действительно, эти слова верны в буквальном смысле. Квантовая механика описывает реальные атомы и, следовательно, всю материю в виде волновых пакетов. Даже в космических масштабах синусоиды представляют собой семена всего сущего. Астрономы исследовали спектр (рисунок синусоидальных волн) космического микроволнового фонового излучения и обнаружили, что эти измерения соответствуют предсказаниям инфляционной космологии — одной из теорий рождения и развития Вселенной. Таким образом, похоже, изначальная синусоида, волнистость в плотности материи и энергии, возникла без Большого взрыва, спонтанно, и породила материю космоса — а также звезды, галактики. И в конечном счете, маленьких детей, катающихся на колесе обозрения.