До того как я узнал, что такое исчисление, я думал, что это что-то необыкновенное. Мой папа говорил о нем с благоговением. Будучи ребенком Великой депрессии, он не смог пойти учиться в колледж, но, возможно, во время пребывания в южной части Тихого океана, ремонтируя двигатели бомбардировщика B-24, он ощутил, на что способно исчисление. Представьте себе несколько зениток с механическим управлением, ведущих автоматический огонь по заходящим на цель истребителям врага. Отец знал, что исчисление здесь использовалось для прицеливания орудий.

Каждый год около миллиона американских студентов проходят курс исчисления. Но мало кто из них действительно понимает, о чем вообще этот курс, или может объяснить, зачем он нужен. Это не их вина. В этом курсе изучается так много методов, которые следует освоить, и так много новых идей, которые необходимо впитать, что легко пропустить общие положения.

Исчисление функций и интегралов — это математика перемен. Она описывает все — от распространения эпидемий до зигзагов крученого мяча в бейсболе. Этот предмет охватывает большой объем материала, и учебники по размеру соответствующие. Многие превышают тысячу страниц, и работать с ними так же приятно, как открывать дверь с дверной пружиной.

Но в этом объемистом фолианте вы обнаружите две идеи, просвечивающие сквозь толщу материала. Все остальное, как любил повторять золотое правило рабби Гиллель, просто комментарии. Эти две идеи — производная и интеграл. Каждая доминирует в своей области исчислений, названных в их честь: дифференциальное и интегральное исчисления.

Грубо говоря, производная расскажет вам, как быстро что-то меняется, а интеграл — сколько это «что-то» накопит. Они родились в разное время и в разных местах: интегралы в Греции около 250 года до н. э., производные — в Англии и Германии в середине XVII века. Тем не менее (поворот в духе романов Диккенса) они оказались кровными родственниками, хотя ученым и потребовалось более двух тысячелетий, чтобы заметить это родство.

В следующей главе мы исследуем столь удивительную связь и понятие интеграла. Но сначала, в рамках подготовительной работы, рассмотрим производные.

Производные существуют вокруг нас, даже если мы не считаем их таковыми. Например, наклон трапа является производной. Как и все производные, он измеряет скорость изменения. В данном случае — на какую высоту за шаг вы поднимаетесь или спускаетесь. Крутой подъем имеет большую производную. У наклона инвалидной коляски с незначительным перепадом она маленькая.

В каждой области практической деятельности есть собственный вариант производной. Будет ли она предельным доходом или темпом роста, скоростью или наклоном — от любого ее названия по-прежнему веет холодком. К сожалению, многие студенты, прослушав курс дифференциального исчисления, приходят к гораздо более узкому толкованию производной как синонима наклона кривой.

Такая путаница понятна и вызвана она тем, что для отображения количественных отношений мы, как правило, применяем графики. Путем графического изображения у как функции от х мы пытаемся представить, как одна переменная влияет на другую. И при этом совершенно не важно, что понимается под скоростью изменения значений на графике. Это могут быть темпы роста вирусов, скорость струи или нечто, что преобразуется в нечто другое, столь же абстрактное, но что можно изобразить как наклон кривой на графике.

Как и наклоны, производные могут быть положительными, отрицательными или равными 0, что указывает на то, что нечто увеличивается, уменьшается или выравнивается. Рассмотрим летящего по воздуху Майкла Джордана, зависшего над корзиной за секунду до одного из своих феноменальных бросков.

Сразу после прыжка его вертикальная скорость (скорость его подъема, изменяющаяся во времени [кстати, еще одна производная]) будет положительной, потому что он поднимается вверх. Высота подъема спортсмена растет. На пути вниз эта производная отрицательная. В самой верхней точке прыжка, где кажется, что Джордан завис в воздухе, а его подъем прекратился, производная равна 0. В этом смысле он действительно висит.

Здесь действует еще один общий принцип: предметы всегда изменяются медленнее в верхней и нижней точках. В Итаке это особенно заметно. В самое темное время зимы дни не только нещадно коротки, но и очень медленно растет продолжительность светового дня. Как только начинается весна, дни быстро удлиняются. Все это вполне объяснимо. Изменения наиболее вялые в крайних точках именно потому, что производная в них равна нулю. В этом случае процессы моментально успокаиваются.

Это свойство нулевой производной проявляется на пиках и во впадинах и лежит в основе ряда практичных способов применения производных, позволяющих выяснить, где функция достигает своего максимума или минимума. Вопрос о максимуме или минимуме возникает, когда мы ищем самый лучший, или самый дешевый, или самый быстрый способ сделать что-либо.

Господин Жоффрей, мой школьный учитель, который вел у нас вводный курс исчислений, умел талантливо преподнести нам условие задач на определение максимума и минимума. Однажды он быстро вбежал в класс и начал рассказывать о своем путешествии через заснеженное поле. Видимо, ветер в одном месте поля намел много снега, покрыв его тяжелым покрывалом, из-за чего учителю пришлось идти гораздо медленнее, а остальная часть поля была чистой, и он шагал по нему легко. В этой ситуации он спросил себя, по какому пути должен идти пешеход, чтобы добраться из пункта А в пункт B как можно быстрее.

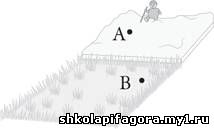
Кто-то думал, что нужно тащиться прямо через глубокий снег, чтобы сократить медленную часть пути. Однако в этом случае оставшаяся часть пути заняла бы больше времени.

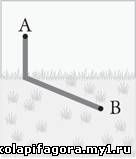
Еще одна стратегия заключалась в том, чтобы идти по прямой от А к В. Это определенно кратчайшее расстояние, но на преодоление его самой трудной части уйдет больше времени.

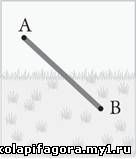
Оптимальный путь можно найти с помощью дифференциального исчисления. Это некий компромисс между перечисленными вариантами.

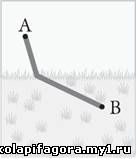
Анализ включает в себя четыре основных этапа. Во-первых, обратите внимание, что общее время в пути, которое мы пытаемся свести к минимуму, зависит от того, где пешеход выбирается из снега. Он может выйти в любом месте, поэтому обозначим как переменную х все возможные точки выхода.

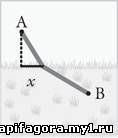
(Ясно, что время в пути зависит также от расположения точек А и В и скорости пешехода в обеих частях поля, но эти параметры заданы. Под контролем пешехода остается только x.)

Во-вторых, с учетом выбора х и известных значений — точки отправления A и пункта назначения B — мы можем вычислить, сколько времени тратит пешеход на путь по быстрой и медленной части поля. Для расчета каждого этапа пути потребуются теорема Пифагора и старая алгебраическая мантра «расстояние равно скорости, умноженной на время». Суммируя пути, проделанные по легкому и трудному участкам, получим формулу для всего времени T пути как функцию от х.

В-третьих, изобразим график зависимости Т от х. В нижней части кривой находится точка, которую мы ищем, соответствующая наименьшему времени пути и, следовательно, самому короткому.

В-четвертых, чтобы найти эту самую нижнюю точку, мы взываем к нулевой производной в соответствии с упомянутым выше принципом. Вычисляем производную от T по х, приравниваем ее к нулю и находим х.

Эти четыре шага требуют знания геометрии, алгебры, а также формул вычисления производных — эти навыки приравниваются к свободному владению иностранным языком, поэтому являются камнем преткновения для многих студентов.

Но окончательный ответ стоит затраченных трудов. Он показывает, что самый быстрый путь подчиняется отношению, известному как закон Снелла. Что? Страшно, что не только свет повинуется этому закону?

Закон Снелла описывает, как преломляются лучи света при переходе из воздуха в воду. Например, когда лучи солнца попадают в бассейн. Свет в воде движется медленнее, так же как и пешеход по снегу, и отклоняется таким образом, чтобы минимизировать время движения. Подобным способом свет преломляется, когда переходит из воздуха в стекло или пластик, что происходит в линзах ваших очков.

Пугает то, что свет ведет себя так, будто он осмысленно изучает все возможные пути, а затем выбирает лучший.